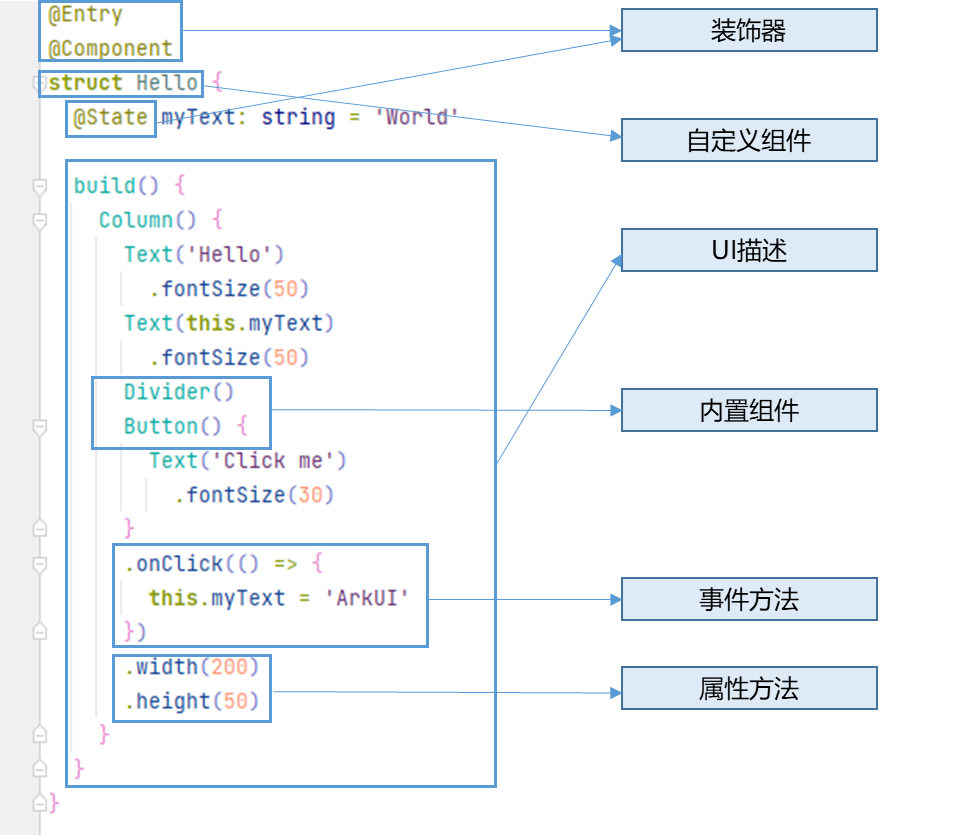
Spatial Data Analysis（四）：空间自相关示例

空间自相关是地理信息科学（GIS）和空间统计学中的重要概念之一，用于研究地理空间上的数据变异性和相关性。空间自相关分析的目标是探讨地理空间中的现象是否呈现出某种程度的空间模式或趋势。在这个过程中，我们关注地理空间中相邻位置之间的数据值之间是否存在某种关联。

以下是关于空间自相关的详细介绍：

1.基本概念：

• 空间自相关：空间自相关是指地理空间上相邻位置的数据值之间的相关性。如果相邻位置的数据值彼此相似，则存在正的空间自相关；如果相邻位置的数据值彼此不同，则存在负的空间自相关。
• 空间权重矩阵：空间自相关的分析通常涉及构建一个空间权重矩阵，该矩阵描述了不同位置之间的空间关系。常见的空间权重矩阵包括邻近矩阵（表示相邻关系）和距离衰减矩阵（表示距离越近，权重越大）。

2.类型：

• 正的空间自相关：相邻位置的数据值之间存在相似性，即一个位置的高（或低）值周围的位置也有高（或低）值。这表明存在集聚现象。
• 负的空间自相关：相邻位置的数据值之间存在差异，即一个位置的高（或低）值周围的位置有低（或高）值。这表明存在分散现象。

3.衡量方法：

• 莫兰指数（Moran’s
  I）：是一种常用的测量空间自相关的统计指标。它考察了空间上的数据分布和空间结构之间的关系。当莫兰指数接近1时，表明正的空间自相关；当接近-1时，表明负的空间自相关；接近0时，表明数据分布呈随机分布。
• 吉特斯指数（Geary’s C）：类似于莫兰指数，用于测量全局空间自相关，其值越小表示越强的正的空间自相关。

4.应用领域：

• 空间自相关广泛应用于地理学、城市规划、环境科学、经济学等领域。
• 在地理信息系统（GIS）中，空间自相关有助于理解地理现象的分布规律，优化资源分配和规划。

5.空间自相关分析的步骤：

• 定义研究区域和空间尺度。
• 构建空间权重矩阵。
• 计算莫兰指数或其他空间自相关指标。
• 进行统计显著性检验，判断空间自相关是否显著。
• 解释结果，理解空间分布的模式。

在本例中，我将使用乔治亚州县级人口普查数据的示例演示如何在 python 中进行空间自相关分析。

具体来说，我们正在绘制县级本科及以上学历人口的百分比，并进行全球/当地莫兰分析。 最后，我们能够识别冷点和热点，帮助我们了解乔治亚州的教育不平等。

Install PySAL packages for SA analysis

pip install -q splot

pip install -q libpysal

Load packages

import numpy as np
import matplotlib.pyplot as plt
import geopandas as gpdfrom libpysal.weights.contiguity import Queen
from splot.esda import moran_scatterplot,plot_moran,lisa_cluster
from esda.moran import Moran, Moran_Local
import splot

Load Georgia dataset

georgia_shp = gpd.read_file("https://raw.githubusercontent.com/Ziqi-Li/GEO4162C/main/data/georgia/G_utm.shp")

First, again check the data we loaded.

georgia_shp.head()

	AREA	PERIMETER	G_UTM_	G_UTM_ID	AREANAME	Latitude	Longitud	TotPop90	PctRural	PctBach	PctEld	PctFB	PctPov	PctBlack	X	Y	AreaKey	geometry
0	9.786480e+08	174967.0	2	1	GA, Rabun County	34.88129	-83.40143	11648	100.0	11.6	17.18	1.13	13.6	0.35	824645.5	3864805	13241	POLYGON ((806227.188 3858275.500, 805577.812 3...
1	4.461530e+08	115140.0	3	2	GA, Towns County	34.91864	-83.73908	6754	100.0	11.4	22.96	1.36	14.0	0.00	797981.7	3872640	13281	POLYGON ((779645.188 3875727.750, 808540.188 3...
2	8.543330e+08	160360.0	4	7	GA, Union County	34.83436	-83.99088	11993	100.0	10.1	17.55	0.88	18.3	0.10	777040.1	3858779	13291	POLYGON ((762005.000 3875204.000, 773345.688 3...
3	1.014270e+09	179577.0	5	4	GA, Fannin County	34.86415	-84.31928	15992	100.0	7.8	17.30	0.58	17.2	0.03	739255.8	3866604	13111	POLYGON ((717121.188 3874113.750, 744454.625 3...
4	8.980900e+08	183295.0	6	3	GA, Murray County	34.78193	-84.74823	26147	89.0	5.5	7.69	0.50	11.3	0.26	707834.3	3854188	13213	POLYGON ((699833.188 3873629.500, 703008.812 3...

georgia_shp.plot()

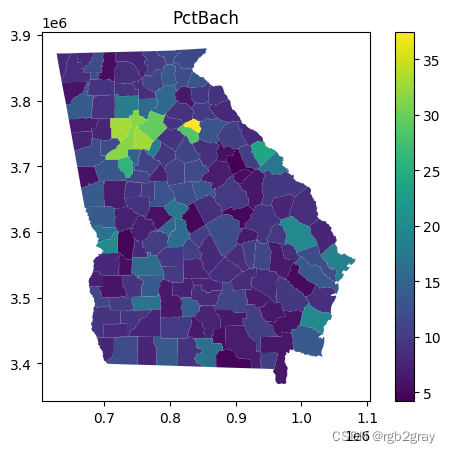
该数据包含一组社会人口变量。 其中之一是“PctBach”，即拥有学士学位或更高学历的人口百分比。

让我们为这个变量创建一个映射。 显然，我们可以看到亚特兰大和雅典附近的巴赫百分比较高。

georgia_shp.plot(column="PctBach",legend=True)
plt.title("PctBach")

Text(0.5, 1.0, 'PctBach')

A map of Georgia for reference
(source:https://www.enchantedlearning.com/usa/states/georgia/map.GIF)

全局 Moran’s I 和 p 值

全局 Moran’s I 是一个用于空间自相关性检测的指标，它可以用于检测空间数据集中的空间聚集现象。具体而言，它可以帮助我们确定空间数据集中的观测点是否具有相似的价值，以及这些点是否出现在一起。

p 值是另一个统计指标，用于评估一个检验结果的显著性。它通常用于确定某个统计检验的结果是否具有统计学意义。

在空间分析中，全局 Moran’s I 和 p 值通常一起使用，以确认空间数据集是否呈现出显著的空间自相关性。如果 Moran’s I 的值接近1且 p 值小于0.05，则可以得出结论，空间数据集呈现出显著的空间自相关性，即空间聚集现象。反之，如果 p 值大于0.05，则可以得出结论，空间数据集中观测点的价值没有表现出统计学上显著的空间自相关性。

指定权重矩阵

w = Queen.from_dataframe(georgia_shp) #Generate W matrix using Queen contiguityw.transform = 'r' #Row-standardization of the weight matrix

('WARNING: ', 65, ' is an island (no neighbors)')<ipython-input-8-385596cab5f3>:1: FutureWarning: `use_index` defaults to False but will default to True in future. Set True/False directly to control this behavior and silence this warningw = Queen.from_dataframe(georgia_shp) #Generate W matrix using Queen contiguity
/usr/local/lib/python3.10/dist-packages/libpysal/weights/weights.py:224: UserWarning: The weights matrix is not fully connected: There are 2 disconnected components.There is 1 island with id: 65.warnings.warn(message)

计算 Moran’s I

from esda.moran import Moranbach = georgia_shp['PctBach'].values #Get the data we are interested.ga_global_moran = Moran(bach, w, permutations = 200) #200 permutations
ga_global_moran.I

0.2487731738404628

p-value

ga_global_moran.p_sim # P value based on permutation tests

0.004975124378109453

这表明 Pct Bach 数据中存在统计显着性 (p=0.005<0.05) 聚类。

莫兰散点图

莫兰散点图是一种用于检测空间自相关性的图表。它可以帮助我们确定数据是否在空间上聚集或分散。在莫兰散点图中，每个点代表一个区域，而每个点周围的点代表邻近区域。如果点之间的距离越近，它们之间的空间滞后就越小。如果点之间的距离越远，它们之间的空间滞后就越大。

要分析莫兰散点图，需要计算莫兰指数。莫兰指数是一种用于测量空间自相关性的统计量。它的值介于-1和1之间。如果莫兰指数为正，则表示数据在空间上聚集。如果莫兰指数为负，则表示数据在空间上分散。如果莫兰指数为0，则表示数据在空间上随机分布。

from splot.esda import plot_moranplot_moran(ga_global_moran, zstandard=False, figsize=(10,4))

/usr/local/lib/python3.10/dist-packages/splot/_viz_esda_mpl.py:354: FutureWarning: `shade` is now deprecated in favor of `fill`; setting `fill=True`.
This will become an error in seaborn v0.14.0; please update your code.sbn.kdeplot(moran.sim, shade=shade, color=color, ax=ax, **kwargs)(<Figure size 1000x400 with 2 Axes>,array([<Axes: title={'center': 'Reference Distribution'}, xlabel='Moran I: 0.25', ylabel='Density'>,<Axes: title={'center': 'Moran Scatterplot (0.25)'}, xlabel='Attribute', ylabel='Spatial Lag'>],dtype=object))

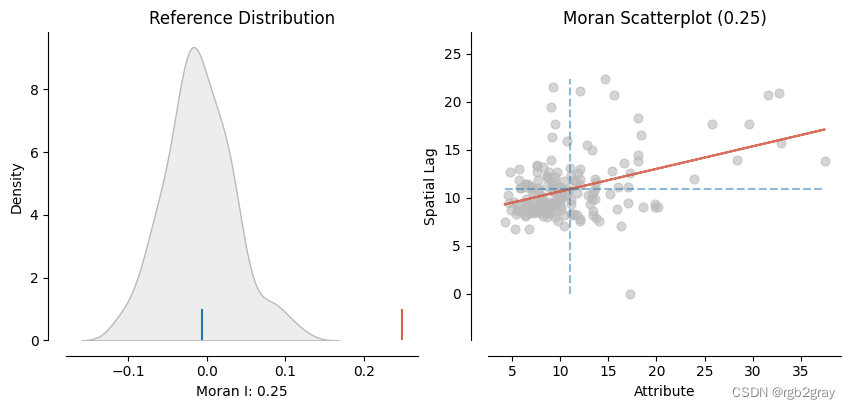
左边是 Moran’s I 的零抽样分布。右边是 Moran 散点图。

生成更好的莫兰散点图，其中包含当地莫兰 Is 的显着性。

对每个县及其所属象限进行颜色编码。

• 红色：HH（高值接近高值）
• 浅蓝色：LH
• 黄色：HL
• 蓝色：LL

from splot.esda import moran_scatterplot
from esda.moran import Moran_Local# calculate Moran_Local and plot
ga_moran_loc = Moran_Local(bach, w,permutations=200)fig, ax = moran_scatterplot(ga_moran_loc, zstandard=False, p=0.05)#Labelling
ax.set_xlabel('Pct Bach')
ax.set_ylabel('Spatial Lag of Pct Bach')

/usr/local/lib/python3.10/dist-packages/esda/moran.py:1059: RuntimeWarning: invalid value encountered in divideself.z_sim = (self.Is - self.EI_sim) / self.seI_simText(0, 0.5, 'Spatial Lag of Pct Bach')

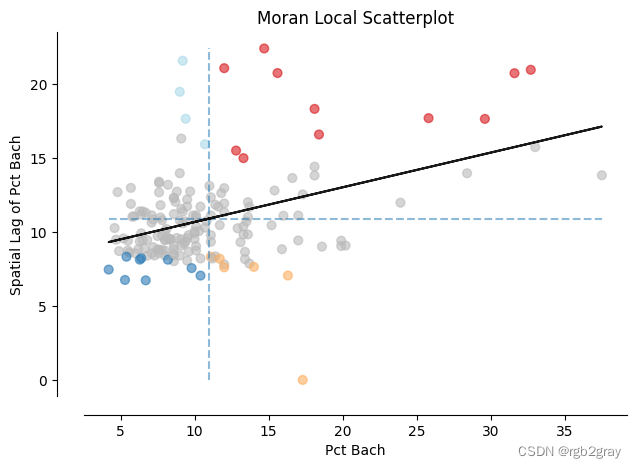
创建热点和冷点地图。

• HH：高 % 巴赫县被高 % 巴赫县包围
• LL：低-低
  左侧：低-高
• HL：高-低
• NS：不显着（p>0.05）

from splot.esda import lisa_clusterlisa_cluster(moran_loc=ga_moran_loc, gdf=georgia_shp, p = 0.05, figsize = (6,6))

(<Figure size 600x600 with 1 Axes>, <Axes: >)

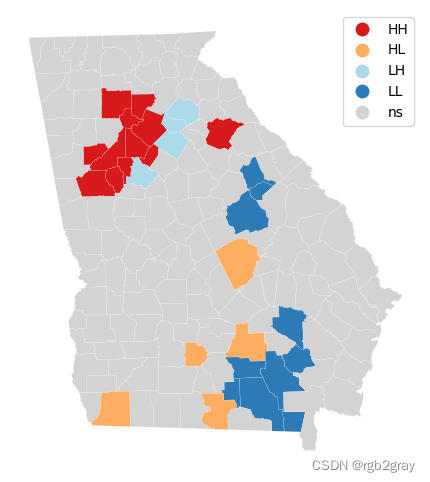
我们可以看到亚特兰大附近有一个统计显着的热点集群。
。