最优化方法复习——线性规划之对偶问题

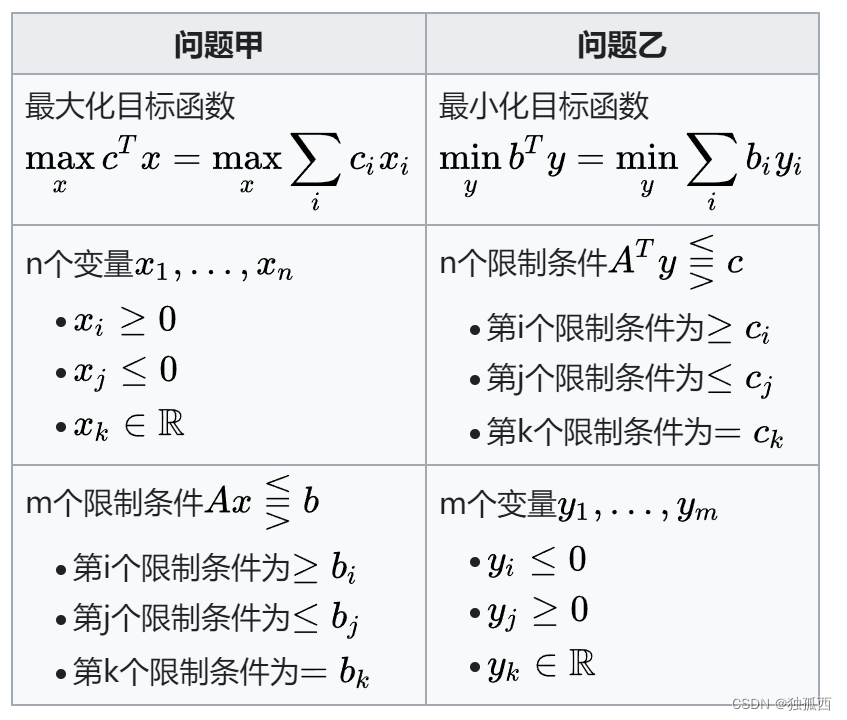
一、线性规划对偶问题定义

原问题：

$\begin{gathered} (LP)\mathrm{Max}\quad z=c^\top x \\ \quad \quad s.t. \quad Ax \leq b \\ \quad \quad \quad \quad x \geq 0 \\ \end{gathered}$

对偶问题：

$\begin{gathered}(DP)\mathrm{Min}\quad f=b^\top y \\ \quad \quad s.t. \quad A^\top y\geq c \\ \quad \quad \quad \quad y\geq0 \\ \end{gathered}$

（1）若一个模型为目标求 “极大”，约束为“小于等于” 的不等式，则它的对偶模型为目标求“极小”，约束是“大于等于”的不等式。即“Max， ≤”和“Min，≥”相对应。

（2）从约束系数矩阵看：一个模型中为Ａ，则另一个模型中为AT 。一个模型是m个约束、 n个变量，则它的对偶模型为 n个约束、m个变量。

（3）从数据b、c的位置看：在两个规划模型中，b和c的位置对换。

（4）两个规划模型中的变量皆非负。

一般称不具有对称形式的一对线性规划为非对称形式的对偶规划。对于非对称形式的规划，可以按照下面的对应关系直接给出其对偶规划。

（1）将模型统一为“Max，≤”或“Min，≥” 的形式，对于其中的等式约束按下面（2）、（3）中的方法处理。

（2）若原规划的某个约束条件为等式约束，则在对偶规划中与此约束对应的那个变量取值没有非负限制。

（3）若原规划的某个变量的值没有非负限制，则在对偶问题中与此变量对应的那个约束为等式。

二、对偶定理与影子价格

定理(弱对偶定理）若 x,y 分别为（LP) 和（DP）的可行解，那么 $c^Tx \leq b^Ty$ 。推论:设（LP）有可行解，那么若（LP）无有界最优解，则（DP）无可行解。
定理 (最优性准则定理) 若 $x^*$ , $y^*$ 分别(LP),(DP)的可行解,且 $c^Tx^* =b^Ty^*$ ，那么 $x^*$ , $y^*$ 分别为(LP)和(DP) 的最优解。
定理(主对偶定理) 若(LP)有最优解，则(DP)也有最优解。反之也成立，且最优值相等。

影子价格是一个向量，它的分量表示最优目标值随相应资源数量变化的变化率。

影子价格反映了不同的局部或个体的增量可以获得不同的整体经济效益。如果为了扩大生产能力，考虑增加设备，就应该从影子价格高的设备入手。这样可以用较少的局部努力，获得较大的整体效益。

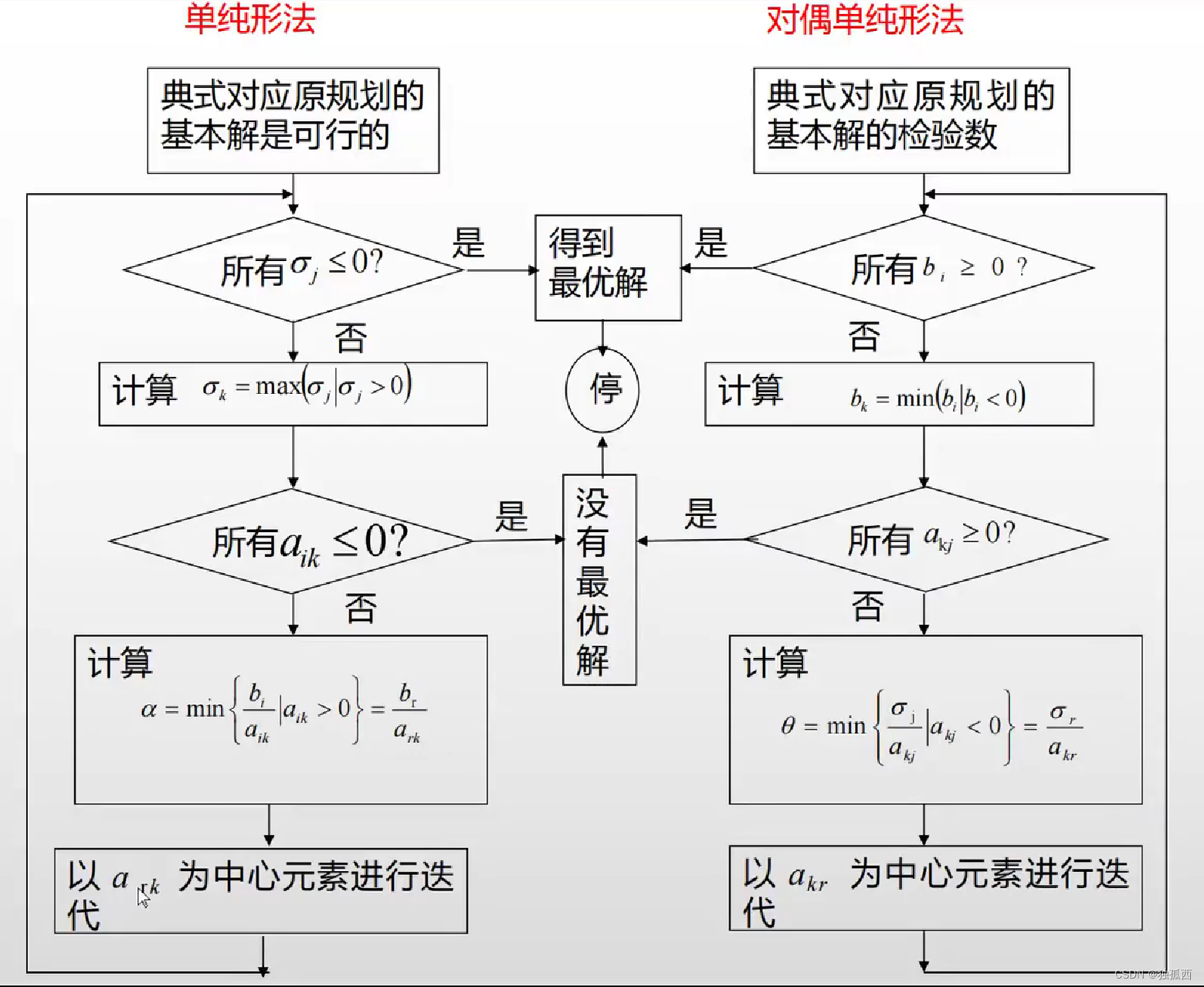
三、对偶单纯形法

1、基本思想

从原规划的一个基本解出发，此基本解不一定可行，但它对应着一个对偶可行解（检验数非正），所以也可以说是从一个对偶可行解出发；然后检验原规划的基本解是否可行，即是否有负的分量，如果有小于零的分量，则进行迭代，求另一个基本解，此基本解对应着另一个对偶可行解（检验数非正）。

如果得到的基本解的分量皆非负，则该基本解为最优解。也就是说，对偶单纯形法在迭代过程中始终保持对偶解的可行性（即检验数非正），使原规划的基本解由不可行逐步变为可行，当同时得到对偶规划与原规划的可行解时，便得到原规划的最优解

什么情况下使用对偶单纯性法呢？

在初始计算中 $\sigma^{T}=(-c^{T},0^{T})\leq0$ ，即对偶可行，但是由于 $-b\leq0$ ,所以 $\begin{cases}x_{s}=-b\leq0\\x=0\end{cases}$ ，所以原问题不可行。

应用前提：有一个基，其对应的基满足:

（1）单纯形表的检验数行全部非正（对偶可行）；

（2）变量取值可有负数（非可行解）。

注：通过矩阵行变换运算，使所有相应变量取值均为非负数即得到最优单纯形表。

2、步骤

（1）建立初始对偶单纯形表,对应一个基本解,所有检验数均非正,转（2）。

（2）若 $b\geq 0$ ,则得到最优解,停止;否则,若有 $b_k<0$ 则选k行的基变量为出基变量,转（3）。

（3）若所有 $a_{kj} \geq 0$ (j = 1,2,…,n)，则原问题无可行解,停止(因为以任何 $a_{kj}$ 为主元做主元消去时，都不可能使 $b_k$ 变为正数); 否则,若有 $a_{kj}<0$ 则选 $\theta=\min\{\sigma_{j}/a_{kj}|a_{kj}<0\}=\sigma_{r}/a_{kr}$ ，那么 $x_r$ 为进基变量,转（4）。