🎃个人专栏：

🐬 算法设计与分析：算法设计与分析_IT闫的博客-CSDN博客

🐳Java基础：Java基础_IT闫的博客-CSDN博客

🐋c语言：c语言_IT闫的博客-CSDN博客

🐟MySQL：数据结构_IT闫的博客-CSDN博客

🐠数据结构：​​​​​​数据结构_IT闫的博客-CSDN博客

💎C++：C++_IT闫的博客-CSDN博客

🥽C51单片机：C51单片机（STC89C516）_IT闫的博客-CSDN博客

💻基于HTML5的网页设计及应用：基于HTML5的网页设计及应用_IT闫的博客-CSDN博客​​​​​​

🥏python：python_IT闫的博客-CSDN博客

🐠离散数学：离散数学_IT闫的博客-CSDN博客

欢迎收看，希望对大家有用！

目录

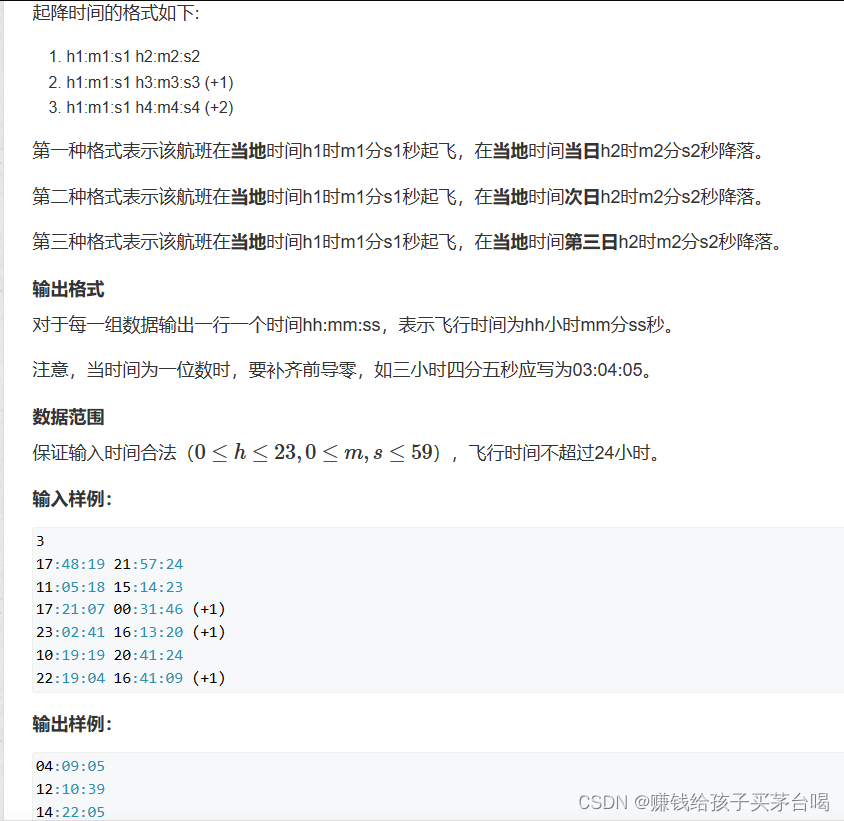
一. 单选题（共15题，82.5分）

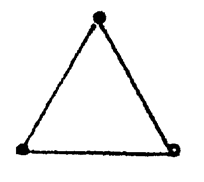
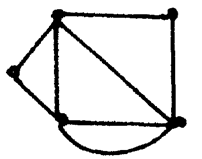
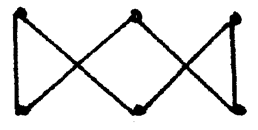
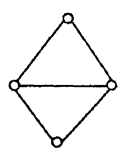
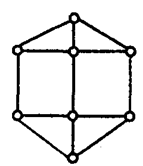
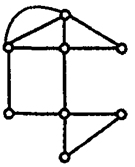
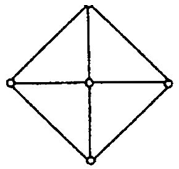
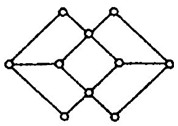
1. (单选题)下列各图不是欧拉图的是（     ）

2. (单选题)下列各图中既是欧拉图，又是汉密尔顿图的是（　　　）

3. (单选题)下图中哪一个是欧拉图？

4. (单选题)下图中哪一个是哈密顿图？

5. (单选题)

6. (单选题)无向图G是欧拉图当且仅当G是连通的且（      ）

7. (单选题)下面既是汉密尔顿图又是欧拉图的图形是（       ）

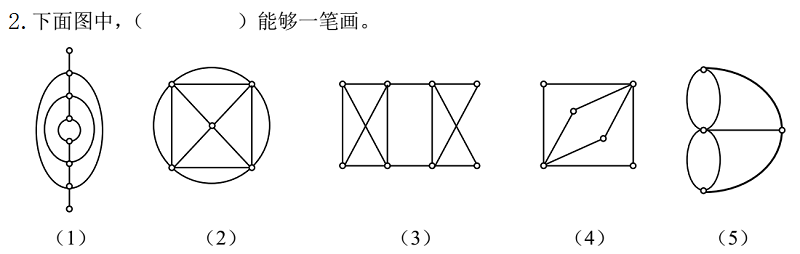
8. (单选题)下列可一笔画成的图形是(     )

9. (单选题)

10. (单选题)一个连通图G具有以下何种条件时，能一笔画出：即从某结点出发，经过图中每边仅一次回到该结点。（   ）

11. (单选题)一个连通的无向图G,如果它的所有结点的度数都是偶数,那么它有一条（    ）

12. (单选题)

13. (单选题)

14. (单选题)无向图G是个欧拉图，那么它们所有的结点度数都是(   )

15. (单选题)欧拉回路是（　　　）

二. 多选题（共1题，5.5分）

16. (多选题)

三. 填空题（共1题，5.5分）

17. (填空题)

四. 判断题（共1题，6.5分）

18. (判断题)连通无向图的欧拉回路经过图中的每个顶点一次且仅一次。

🎯答案：

---

一. 单选题（共15题，82.5分）

1. (单选题)下列各图不是欧拉图的是（     ）

• A. 

  

• B. 

  

• C. 

  

• D. 

  

2. (单选题)下列各图中既是欧拉图，又是汉密尔顿图的是（　　　）

• A. 

  

• B. 

  

• C. 

  

• D. 

  

3. (单选题)下图中哪一个是欧拉图？

• A. K3,3
• B. K3,4
• C. K4
• D. K4,4

4. (单选题)下图中哪一个是哈密顿图？

• A. K1，1
• B. K2
• C. k3,4
• D. K5

5. (单选题)

• A. ｛(a,d) }是割边
• B. ｛(a,d) }是边割集
• C.

  ｛(d，e) }是边割集

• D. ｛(a,d),(a,c) }是边割集

6. (单选题)无向图G是欧拉图当且仅当G是连通的且（      ）

• A.

  G中各顶点的度数均相等

• B.

  G中各顶点的度数之和为偶数

• C.

  G中各顶点的度数均为偶数

• D.

  G中各顶点的度数均为奇数

7. (单选题)下面既是汉密尔顿图又是欧拉图的图形是（       ）

• A. 

  

• B. 

  

• C. 

  

• D. 

  

8. (单选题)下列可一笔画成的图形是(     )

• A. 

  

• B. 

  

• C. 

  

• D. 

  

9. (单选题)

• A. 1
• B. 2
• C. 3
• D. 4

10. (单选题)一个连通图G具有以下何种条件时，能一笔画出：即从某结点出发，经过图中每边仅一次回到该结点。（   ）

• A. G没有奇数度结点
• B. G有1个奇数度结点
• C. G有2个奇数度结点
• D. G没有或有2个奇数度结点

11. (单选题)一个连通的无向图G,如果它的所有结点的度数都是偶数,那么它有一条（    ）

• A. 汉密尔顿回路
• B. 欧拉回路
• C. 欧拉通路
• D. 汉密尔顿通路

12. (单选题)

设G是n个顶点的无向简单图，则下列说法不正确的是  （       ）

• A. 若G是欧拉图，则其边数大于n-1
• B. 若G是欧拉图，则G中必有割边
• C. 若G中有欧拉通路，则G是连通图，且有零个或两个奇度数顶点
• D. 若G中任意一对顶点的度数之和大于等于n-1，则G中有汉密尔顿通路

13. (单选题)

• A. 1
• B. 2
• C. 3
• D. 4

14. (单选题)无向图G是个欧拉图，那么它们所有的结点度数都是(   )

• A. 偶数
• B. 奇数
• C. 任意整数
• D. 大于等于2

15. (单选题)欧拉回路是（　　　）

• A. 路径
• B. 简单回路
• C. 既是初级回路也是简单回路
• D. 既非初级回路也非简单回路

二. 多选题（共1题，5.5分）

16. (多选题)

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5

三. 填空题（共1题，5.5分）

17. (填空题)

已知图G 中有1个1度结点，2个2度结点，3个3度结点，4个4度结

点，则G 的边数是

四. 判断题（共1题，6.5分）

18. (判断题)连通无向图的欧拉回路经过图中的每个顶点一次且仅一次。

• A. 对
• B. 错

🎯答案：

1-5：BCDDC

6-10：CBADA

11-15：BBCAB

16：CD

17：15

18：错