SLAM算法与工程实践系列文章

下面是SLAM算法与工程实践系列文章的总链接，本人发表这个系列的文章链接均收录于此

SLAM算法与工程实践系列文章链接

---

下面是专栏地址：

SLAM算法与工程实践系列专栏

---

文章目录

• SLAM算法与工程实践系列文章
• • SLAM算法与工程实践系列文章链接
  • SLAM算法与工程实践系列专栏
• 前言
• SLAM算法与工程实践——SLAM基本库的安装与使用（6）：g2o优化库（4）
• • 初步认识图的边
  • 如何自定义边
  • 如何向图中添加边
  • • 添加一元边
    • 添加二元边
  • 补充

---

前言

这个系列的文章是分享SLAM相关技术算法的学习和工程实践

---

SLAM算法与工程实践——SLAM基本库的安装与使用（6）：g2o优化库（4）

初步认识图的边

3种类型——BaseUnaryEdge、BaseBinaryEdge和BaseMultiEdge，它们分别表示一元边、二元边和多元边。

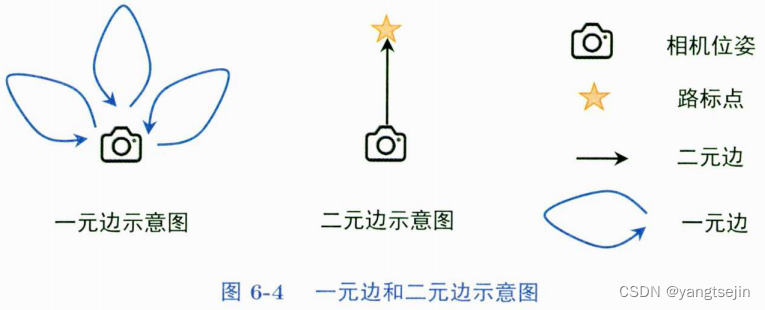
通常是二元边为主

比如我们用边表示三维点投影到图像平面上的重投影误差，就可以设置如下输入参数。

BaseBinaryEdge<2,Vector2D,VertexSBAPointXYZ,VertexSE3Expmap>

BaseBinaryEdge类型的边是一个二元边。

第1个参数“2”是说测量值是二维的，测量值就是图像的二维像素坐标，对应测量值的类型是Vector2D，边连接的两个顶点分别是三维点 VertexSBAPointXYZ 和李群位姿 VertexSE3Expmap

常用的函数，成员变量

// 读/写函数，一般情况下不需要进行读/写操作，仅声明一下就可以
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;// 使用当前顶点的值计算的测量值与真实的测量值之间的误差
virtual void computeError ();//误差对优化变量的偏导数，也就是我们说的 Jacobian
virtual void linearizeoplus ();// 几个重要的成员变量和函数
_measurement		// 存储观测值
_error					// 存储计算的误差
_vertices[]			// 存储顶点信息setVertex(int,vertex)		// 定义顶点及其编号
setId(int)		// 定义边的编号
setMeasurement(type)		// 定义观测值
setInformation()		// 定义信息矩阵

如何自定义边

g2o中边的模板

//g2o中边的定义格式
class myEdge:public g2o:BaseBinaryEdge<errorDim,errorType,Vertex1Type,Vertex2Type>
{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWmyEdge(){}// 读/写函数virtual bool read(istream& in){}virtual bool write(ostream& out) const {}//误差=测量值-估计值virtual void computeError() override{_error = _measurement - /*估计值*/；}//增量计算函数：误差对优化变量的偏导数virtual void linearizeOplus() override{_jacobianoplusxi(pos,pos)=something;_jocobianOplusxj(pos,pos)=something;}
}

曲线拟合中一元边的简单例子

//曲线拟合中一元边的简单例子
class CurveFittingEdge:public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWCurveFittingEdge(double x) : BaseUnaryEdge (), _x(x){}//计算曲线模型误差void computeError(){const CurveFittingVertex* v = static_cast<const CurveFittingVertex*>(vertices[0]);const Eigen::Vector3d abc = v->estimate();//曲线模型为a*×^2+b*x+c//误差=测量值-估计值_error(0,0) = _measurement - std:exp(abc(0,0)*_x*_x + abc(1,0)*x + 
abc(2,0));}//读/写函数virtual bool read(istream& in){}virtual bool write (ostream& out) const {}public:double _x;
};  

稍微复杂的例子，涉及3D-2D点的PP问题，也就是最小化重投影误差问题

// g2o/types/sba/edge project xyz2uv.h,g2o/types/sba/edge project xyz2uv.cpp
// PnP问题中三维点投影到二维图像上二元边定义示例
class g2o_TYPES_SBA_API EdgeProjectXYZ2UV : public BaseBinaryEdge<2,Vector2,VertexPointXYZ,VertexSE3Expmap>
{public:EIGEN MAKE ALIGNED OPERATOR NEW;
EdgeprojectXYZ2UV();//读/写函数bool read(std:istream& is);bool write(std::ostream& os) const;//计算误差void computeError();//增量计算函数virtual void linearizeOplus();//相机参数CameraParameters* _cam;
};void EdgeProjectXYZ2UV::computeError()
{//将顶点中李群相机位姿记为v1const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);//将顶点中三维点记为v2const VertexPointXYZ* v2 = static_cast<const VertexPointXYZ*>(vertices[0]);
const CameraParameters*cam static cast<const CameraParameters*>
(parameter(0));//误差=测量值-估计值_error = measurement()- cam->cam_map(v1->estimate().map(v2->estimate()));
}// 增量计算函数：误差对优化变量的偏导数
void EdgeprojectXYZ2UV::linearizeOplus()
{VertexSE3Expmap* vj = static_cast<VertexSE3Expmap*>(vertices[1]);SE3Quat T(vj->estimate());VertexPointXYZ* vi = static_cast<VertexPointXYZ*>(vertices[0]);Vector3 xyz = vi->estimate();Vector3 xyz_trans = T.map(xyz);number_t x = xyz_trans[0];number_t y = xyz_trans[1];number_t z = xyz_trans[2];number_t z_2 = z * z;const CameraParameters* cam = static_cast<const CameraParameters*>(parameter(0));//重投影误差关于三维点的雅可比矩阵Eigen::Matrix<number_t,2,3,Eigen::ColMajor> tmp;tmp(0,0) = cam->focal_length;tmp(0,1) = 0:tmp(0,2) = -x / z * cam->focal_length;tmp(1,0) = 0;tmp(1,1) = cam->focal_length;tmp(1,2) = -y / z * cam->focal_length;_jacobianOplusXi = -1. / z * tmp * T.rotation().toRotationMatrix();//重投影误差关于相机位姿的雅可比矩阵_jacobianOplusXj(0,0) = x * y / z_2 * cam->focal_length;_jacobianOplusXj(0,1) = -(1 + (x * x / z_2)) * cam->focal_length;_jacobianOplusXj(0,2) = y / z * cam->focal_length;_jacobianOplusXj(0,3) = -1. / z * cam->focal_length;_jacobianOplusXj(0,4) = 0;_jacobianOplusXj(0,5) = x / z_2 * cam->focal_length;_jacobianOplusXj(1,0) = (1 + y * y / z_2) * cam->focal_length;_jacobianOplusXj(1,1) = -x * y / z_2 * cam->focal_length;_jacobianOplusXj(1,2) = -x / z * cam->focal_length;_jacobianOplusXj(1,3) = 0;_jacobianOplusXj(1,4) = -1./ z * cam->focal_length;_jacobianOplusXj(1,5) = y /z_2 * cam->focal_length;
}

其中有一些比较难理解的地方，我们分别解释。

首先是误差的计算：

//误差=测量值-估计值
_error = measurement()- cam->cam_map(v1->estimate().map(v2->estimate()));

这里的本质是误差 = 测量值 - 估计值。下面梳理一下思路。

我们先来看 cam_map 函数，它的功能是把相机坐标系下的三维点（输入）用内参转换为图像坐标（输出），具体定义如下。

// g2o/types/sba/types_six_dof_expmap.cpp
// cam_map函数定义
Vector2 CameraParameters::cam_map(const Vector3 & trans_xyz) const{Vector2 proj = project2d(trans_xyz);Vector2 res;res[0] = proj[0]*focal_length + principle_point[0];res[1] = proj[1]*focal_length + principle_point[1];return res;
}

然后看 map 函数，它的功能是把世界坐标系下的三维点转换到相机坐标系下，定义如下

// g2o/types/sim3/sim3.h
// map函数定义
Vector3 map (const Vector3& xyz) const
{return s*(r*xyz)+t;
}

因此，下面的代码就是用 v1 估计的位姿把 v2 代表的三维点转换到相机坐标系下。

v1->estimate().map(v2->estimate())

linearizeOplus() 重投影误差关于相机位姿的雅可比矩阵为
$$\frac{\partial \mathbf{e}}{\partial \delta \mathbf{\xi }}=\left[\begin{array}{cccccc}\frac{f_{x}XY}{Z^2}& -f_x-\frac{f_x{X}^2}{Z^2}& \frac{f_{x}Y}{Z}& -\frac{f_x}{Z}& 0& \frac{f_{x}X}{Z^2}\\ & & & & & \\ f_y+\frac{f_y{Y}^2}{Z^2}& -\frac{f_{y}XY}{Z^2}& -\frac{f_{y}X}{Z}& 0& -\frac{f_y}{Z}& \frac{f_{y}Y}{Z^2}\end{array}\right]$$

重投影误差关于三维点的雅可比矩阵为
$$\frac{\partial \mathbf{e}}{\partial \mathbf{P}}=-\left[\begin{array}{ccc}\frac{f_x}{Z}& 0& -\frac{f_{x}X}{Z^2}\\ & & \\ 0& \frac{f_y}{Z}& -\frac{f_{y}Y}{Z^2}\end{array}\right]\mathbf{R}$$
上述矩阵与函数 EdgeProjectXYZ2UV::computeError()中的实现是一一匹配的。

如何向图中添加边

添加一元边

先来看一元边的添加方法，仍然以曲线拟合的例子来说明。

添加一元边示例：曲线拟合

// 添加一元边示例：曲线拟合
for int i=0;i<N;i++)
{CurveFittingEdge* edge = new CurveFittingEdge(x_data[i])edge->setId(i);	//设置边的IDedge->setVertex(0,v);	//设置连接的顶点v,其编号为0edge->setMeasurement(y_data[i]);	//设置观测的数值edge->setInformation(Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma * w_sigma)); 		//信息矩阵optimizer.addEdge(edge);		//将边添加到优化器
}

setMeasurement 函数输入的观测值具体指什么？

对于这个曲线拟合的例子来说，观测值就是实际观测到的数据。对于视觉SLAM来说，观测值通常就是我们观测到的特征点坐标。

添加二元边

添加二元边示例：PnP投影

// 添加二元边示例：PnP投影
// 顶点包括地图点和位姿
index = 1;
// points_2d是由二维图像特征点组成的向量
for (const Point2f p:points_2d)
{g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();		// 设置边的IDedge->setId(index);// 设置边连接的第1个顶点：三维地图点edge->setVertex(0,dynamic_cast<g2o::VertexSBAPointXYZ*>(optimizer.vertex(index)));// 设置边连接的第2个顶点：位姿edge->setVertex(1,pose);// 设置观测：图像上的二维特征点坐标edge->setMeasurement(Eigen::Vector2d (p.x,p.y));// 设置信息矩阵edge->setInformation(Eigen::Matrix2d::Identity());// 将边添加到优化器中optimizer.addEdge(edge);//添加边的IDindex++;
}

这里的 setMeasurement 函数中的 p 来自由特征点组成的向量 points_2d，也就是特征点的图像坐标(x,y)

另外，setVertex 有两个，一个是 0 和 VertexSBAPointXYZ 类型的顶点，另一个是 1 和 pos。

这里的0和1是什么意思？能否互换呢？

这里的0和1分别指代顶点的ID，能不能互换可能需要查看顶点定义部分的代码。

setVertex在g2o中的定义。

// g2o/core/hyper_graph.h
// set the ith vertex on the hyper-edge to the pointer supplied
void setVertex(size_t i,Vertex*v)
{assert(i<vertices.size() && "index out of bounds");_vertices[i]=v;
}

_vertices[i] 中的 i 对应的就是这里的 0 和 1。代码中的类型 g2o::EdgeProjectXYZ2UV 的定义如下。

class g2o_TYPES_SBA_API EdgeProjectXYZ2UV
{// ......// 相机位姿v1const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);// 三维点v2const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*> (_vertices[0]);// ......
}

vertices[0] 对应的是 VertexSBAPointXYZ 类型的顶点，也就是三维点。

vertices[1] 对应的是 VertexSE3Expmap 类型的顶点，也就是位姿pose。

因此，前面1对应的应该是pos，0对应的应该是三维点。所以，这个ID绝对不能互换

补充

static_cast 和 dynamic_cast 是C++中两种不同类型的类型转换操作符，它们在类型转换时的用途和行为有着显著的差异。

1. static_cast

   • 用途：static_cast 主要用于进行基本数据类型之间的转换（如 int 转 float）、类层次结构中基类和派生类指针或引用之间的转换（向上转型），以及具有转换构造函数或类型转换运算符的类之间的转换。

   • 行为：static_cast 在编译时执行所有检查。如果转换是不合法的，编译器将报错。然而，它不进行运行时类型检查。这意味着，当你将派生类指针或引用向下转型为基类指针或引用时，static_cast 不会检查转换的安全性。

   • 例子：

     float f = 3.5;
     int i = static_cast<int>(f); // 将 float 转换为 int
     

2. dynamic_cast

   • 用途：dynamic_cast 主要用于类层次结构中，尤其是进行向下转型（从基类指针或引用转换为派生类指针或引用）时。它被用于那些需要在运行时检查对象类型的情况。

   • 行为：dynamic_cast 进行运行时类型检查，确保安全地进行向下转型。如果转换不合法或不安全，dynamic_cast 会返回空指针（对于指针类型）或抛出异常（对于引用类型）。

   • 例子：

     class Base { /* ... */ };
     class Derived : public Base { /* ... */ };
     Base* b = new Derived();
     Derived* d = dynamic_cast<Derived*>(b); // 运行时检查
     

总结：

• static_cast 更适合那些在编译时就能确定安全性的转换，如基本数据类型转换或向上转型。
• dynamic_cast 主要用于需要运行时类型检查的情况，特别是在向下转型时。
• 使用 dynamic_cast 需要额外的运行时开销，因为它涉及到类型的运行时检查。而 static_cast 不涉及运行时检查，因此性能更好，但可能牺牲了安全性。

关于指针方面的 static_cast 和 dynamic_cast 的具体差异，可以从以下几个方面进行详细说明：

1. 向上转型（Upcasting）：

   • static_cast:

     • 安全地将派生类的指针或引用转换为基类的指针或引用。

     • 这种转换是安全的，因为派生类对象总是包含基类部分。

     • 示例：

       class Base {};
       class Derived : public Base {};
       Derived *d = new Derived();
       Base *b = static_cast<Base*>(d); // 安全的向上转型
       

   • dynamic_cast:

     • 也可以用于向上转型，但这通常没有必要，因为编译器会隐式进行这种转换。

     • 示例：

       Derived *d = new Derived();
       Base *b = dynamic_cast<Base*>(d); // 向上转型，但通常不必要
       

2. 向下转型（Downcasting）：

   • static_cast:

     • 可以将基类的指针或引用转换为派生类的指针或引用。

     • 这种转换不安全，因为没有运行时检查来确保转换的有效性。

     • 如果使用不当，可能会导致未定义行为。

     • 示例：

       Base *b = new Derived();
       Derived *d = static_cast<Derived*>(b); // 不安全的向下转型
       

   • dynamic_cast:

     • 安全地进行向下转型。

     • 在运行时检查对象是否真的是指定的派生类类型。

     • 如果转换不合法，对于指针类型返回空指针，对于引用类型抛出异常。

     • 需要基类中至少有一个虚函数（通常是虚析构函数）。

     • 示例：

       Base *b = new Derived();
       Derived *d = dynamic_cast<Derived*>(b); // 安全的向下转型
       if (d) {// 转换成功
       } else {// 转换失败
       }
       

3. 性能：

   • static_cast:
     • 由于没有运行时类型检查，性能较好。
   • dynamic_cast:
     • 需要运行时类型信息（RTTI），因此相比 static_cast 有一定的性能开销。

4. 适用场景：

   • 使用 static_cast 当你确定转换是安全的，并且了解你正在做的事情。
   • 使用 dynamic_cast 当你需要在运行时检查类型安全性，特别是在你不确定对象是否为某个派生类类型的时候。

总之，选择这两者之间的适当转换取决于你的具体需求，以及你对类型安全和性能的考量。在实际编程中，正确使用类型转换对于保证程序的正确性和稳定性至关重要。