基于果蝇算法优化的Elman神经网络数据预测

基于果蝇算法优化的Elman神经网络数据预测 - 附代码

文章目录

基于果蝇算法优化的Elman神经网络数据预测 - 附代码
- 1.Elman 神经网络结构
- 2.Elman 神经用络学习过程
- 3.电力负荷预测概述
- - 3.1 模型建立
- 4.基于果蝇优化的Elman网络
- 5.测试结果
- 6.参考文献
- 7.Matlab代码

摘要：针对Elman神经网络，初始权值阈值盲目随机性的缺点。采用果蝇算法对ELman的阈值和权值进行优化。利用电力负荷预测模型进行测试，结果表明改进后的神经网络预测性能更佳。

1.Elman 神经网络结构

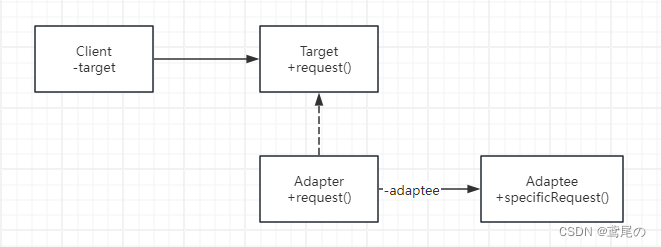
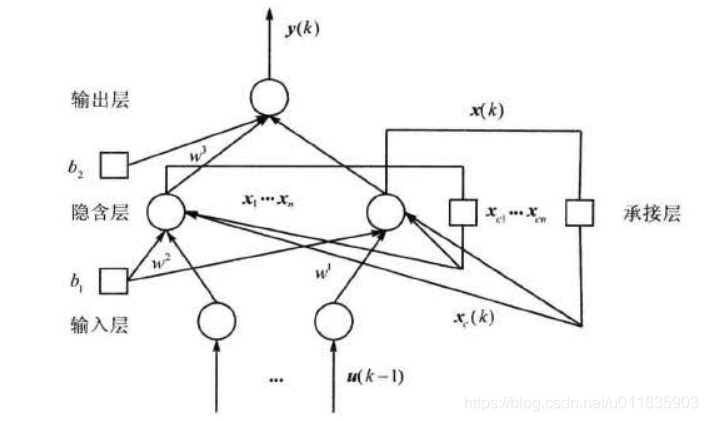
Elman 型神经网络一般分为四层：输入层、隐含层（中间层)、承接层和输出层。如图 1所示。输入层、隐含层、输出层的连接类似于前馈式网络，输入层的单元仅起信号传输作用，输出层单元起线性加权作用。隐含层单元的传递函数可采用线性或非线性函数，承接层又称上下文层或状态层，它用来记忆隐含层单元前一时刻的输出值并返回给网络的输入，可以认为是一个一步延时算子。

Elman 神经网络的特点是隐含层的输出通过承接层的延迟与存储，自联到隐含层的输入。这种自联方式使其对历史状态的数据具有敏感性，内部反馈网络的加入增强了网络本身处理动态信息的能力，从而达到动态建模的目的。此外， Elman 神经网络能够以任意精度逼近任意非线性映射，可以不考虑外部噪声对系统影响的具体形式，如果给出系统的输入输出数据对，就可以对系统进行建模。

在这里插入图片描述

图1.Elman网络结构

2.Elman 神经用络学习过程

以图1为例， Elman 网络的非线性状态空间表达式为 :
$g(w^3x(k)) \tag{1}$

$x(k)=f(w^1x_c(k)+w^2(u(k-1)))\tag{2}$

$x_c(k)=x(k-1)\tag{3}$

式中， $y$ 为 $m$ 维输出结点向量； $x$ 为 $n$ 维中间层结点单元向量； $u$ 为 $r$ 维输入向量； $x_c$ 为 $n$ 维反馈状态向量； $w^3$ 为中间层到输出层连接权值； $w^2$ 为输入层到中间层连接权值； $w^1$ 为承接层到中间层的连接权值； $g (*)$ 为输出神经元的传递函数，是中间层输出的线性组合； $f (*)$ 为中间层神经元的传递函数，常采用 $S$ 函数。

Elman 神经网络也采用 BP 算法进行权值修正，学习指标函数采用误差平方和函数。
$E(w)=\sum_{k=1}^n(y_k(w)-y'_k(w))^2\tag{4}$

3.电力负荷预测概述

电力系统由电力网、电力用户共同组成，其任务是给广大用户不间断地提供经济、可靠、符质量标准的电能，满足各类负荷的需求，为社会发展提供动力。由于电力的生产与使用具有特殊性，即电能难以大量储存，而且各类用户对电力的需求是时刻变化的，这就要求系统发电出力应随时与系统负荷的变化动态平衡，即系统要最大限度地发挥出设备能力，使整个系统保持稳定且高效地运行，以满足用户的需求。否则，就会影响供用电的质量，甚至危及系统的安全与稳定。因此，电力系统负荷预测技术发展了起来，并且是这一切得以顺利进行的前提和基础。负荷预测的核心问题是预测的技术问题，或者说是预测的数学模型。传统的数学模型是用现成的数学表达式加以描述，具有计算量小、速度快的优点，但同时也存在很多的缺陷和局限性，比如不具备自学习、自适应能力、预测系统的鲁棒性没有保障等。特别是随着我国经济的发展，电力系统的结胸日趋复杂，电力负荷变化的非线性、时变性和不确定性的特点更加明显，很难建立一个合适的数学模型来清晰地表达负荷和影响负荷的变量之间的关系。而基于神经网络的非数学模型预测法，为解决数学模型法的不足提供了新的思路。

3.1 模型建立

利用人工神经网络对电力系统负荷进行预测，实际上是利用人工神经网络可以以任意精度逼近任一非线性函数的特性及通过学习历史数据建模的优点。而在各种人工神经网络中，反馈式神经网络又因为其具有输入延迟，进而适合应用于电力系统负荷预测。根据负荷的历史数据，选定反馈神经网络的输入、输出节点，来反映电力系统负荷运行的内在规律，从而达到预测未来时段负荷的目的。因此，用人工神经网络对电力系统负荷进行预测，首要的问题是确定神经网络的输入、输出节点，使其能反映电力负荷的运行规律。

一般来说，电力系统的负荷高峰通常出现在每天的 9～ 19 时之间，本案对每天上午的逐时负荷进行预测，即预测每天 9 ～ 11 时共 3 小时的负荷数据。电力系统负荷数据如下表所列，表中数据为真实数据，已经经过归一化。

时间	负荷数据	负荷数据	负荷数据
2008.10.10	0.1291	0.4842	0.7976
2008.10.11	0.1084	0.4579	0.8187
2008.10.12	0.1828	0.7977	0.743
2008.10.13	0.122	0.5468	0.8048
2008.10.14	0.113	0.3636	0.814
2008.10.15	0.1719	0.6011	0.754
2008.10.16	0.1237	0.4425	0.8031
2008.10.17	0.1721	0.6152	0.7626
2008.10.18	0.1432	0.5845	0.7942

利用前 8 天的数据作为网络的训练样本，每 3 天的负荷作为输入向量，第 4 天的负荷作为目标向量。这样可以得到 5 组训练样本。第 9 天的数据作为网络的测试样本，验证网络能否合理地预测出当天的负荷数据。

4.基于果蝇优化的Elman网络

果蝇算法原理请参考：https://blog.csdn.net/u011835903/article/details/108344654

利用果蝇算法对Elman网络的初始权值和阈值进行优化。适应度函数设计为测试集的绝对误差和：
$\sum_{i=1}^n|predict_n - TrueValue_n| \tag{5}$

5.测试结果

果蝇参数设置如下：

%% 网络相关参数设定
hiddNum = 18;%隐含层个数
R = size(p_train,1);%输入数据每组的维度
Q = size(t_train,1);%输出数据的维度
threshold = [0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1];%每组数据对应维度的最小（0）和最大值（1）;%% 果蝇相关参数设定
%% 定义果蝇优化参数
pop=20; %种群数量
Max_iteration=20; %  设定最大迭代次数
dim = hiddNum*R + hiddNum + Q + hiddNum*hiddNum + Q*hiddNum;%维度，即权值与阈值的个数，承接层个数
lb = -5.*ones(1,dim);%下边界
ub = 5.*ones(1,dim);%上边界
fobj = @(x) fun(x,hiddNum,R,Q,threshold,p_train,t_train,p_test,t_test);