LC 2397. 被列覆盖的最多行数

2397. 被列覆盖的最多行数

文章目录

2397. 被列覆盖的最多行数
- 二进制枚举
- - 代码实现：
- 递归回溯实现
- - 代码实现
- Gosper's Hack
- - 代码实现

难度：中等

题目大意：

给你一个下标从 0 开始、大小为 m x n 的二进制矩阵 matrix ；另给你一个整数 numSelect，表示你必须从 matrix 中选择的不同列的数量。

如果一行中所有的 1 都被你选中的列所覆盖，则认为这一行被覆盖了。

形式上，假设 s = {c1, c2, ...., cnumSelect} 是你选择的列的集合。对于矩阵中的某一行 row ，如果满足下述条件，则认为这一行被集合 s 覆盖：

对于满足 matrix[row][col] == 1 的每个单元格 matrix[row][col]（0 <= col <= n - 1），col 均存在于 s 中，或者
row 中 不存在 值为 1 的单元格。

你需要从矩阵中选出 numSelect 个列，使集合覆盖的行数最大化。

返回一个整数，表示可以由 numSelect 列构成的集合覆盖的 最大行数 。

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 12
matrix[i][j] 要么是 0 要么是 1
1 <= numSelect <= n

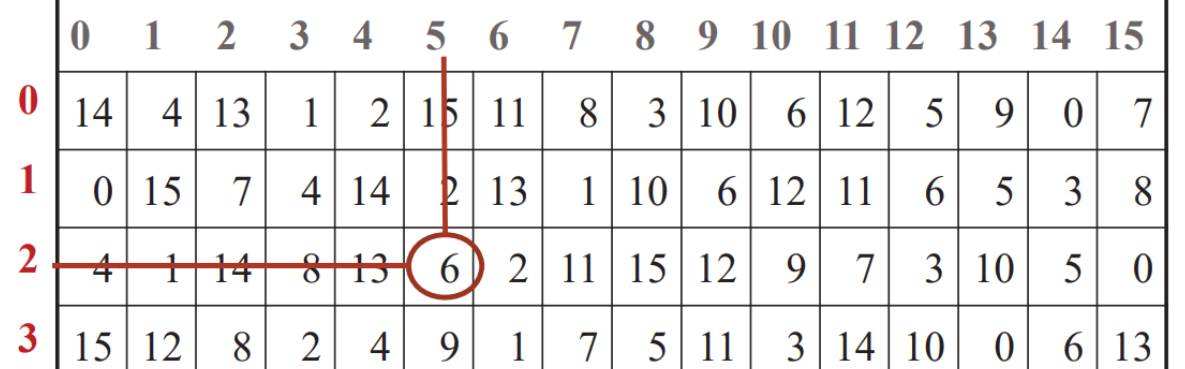
输入：matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出：3
解释：
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖，因为其中没有出现 1 。
- 第 1 行被覆盖，因为值为 1 的两列（即 0 和 2）均存在于 s 中。
- 第 2 行未被覆盖，因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖，因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此，可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行，但可以证明无法覆盖更多行。

根据题目给的数据范围，这题很显然可以暴力解决

二进制枚举

每一行都有两种情况，就是选和不选，我们可以用一个二进制来表示这个状态，比如说10，注意二进制是从右往左读，所以就可以知道这个状态表示的就是第0列是不选的1代表第一列选的，依据这样的思路，所以一共有1 << m种状态，但是并不是每一种状态都是满足要求的，因为题目要求的是一定要有numSelect个1，所以我们只需要进行额外的判断即可

二进制枚举的板子：

for (int i = 0; i < 1 << n; i ++) {for (int j = 0; j < 31; j ++) { // 对当前状态进行操作if (i >> j & 1) ... //判断这个状态的第j位是不是1...}...
}

代码实现：

class Solution {
public:bool check(int n, int numSelect) {int res = 0;for (int i = 0; i < 31; i ++) {if (n >> i & 1) res ++;}return res == numSelect;}int maximumRows(vector<vector<int>>& matrix, int numSelect) {int n = matrix.size(), m = matrix[0].size();int res = 0;for (int i = 0; i < 1 << m; i ++) {if (check(i, numSelect)) {int t = 0;for (int k = 0; k < n; k ++) {bool fl = true;for (int j = 0; j < m; j ++) {if ((i >> j & 1) || !matrix[k][j]) continue;fl = false;break;}if (fl) t ++;}res = max(res, t);}}return res;}
};

时间复杂度: $O(nm2^m)$

递归回溯实现

我们可以将上面的代码翻译成递归形式，下面代码实现

代码实现

class Solution {
public:int maximumRows(vector<vector<int>>& matrix, int numSelect) {int n = matrix.size(), m = matrix[0].size();bool st[m];memset(st, 0, sizeof st);int res = 0;function<void(int, int)> dfs = [&](int u, int sum) -> void {if (u >= m) return;st[u] = true;if (sum + 1 == numSelect) {int t = 0;for (int i = 0; i < n; i ++) {bool fl = true;for (int j = 0; j < m; j ++) {if (st[j] || !matrix[i][j]) continue;fl = false;break;}if (fl) t ++;}res = max(res, t);}dfs(u + 1, sum + 1); // 选st[u] = false; // 回溯dfs(u + 1, sum); // 不选};dfs(0, 0);return res;}
};

时间复杂度和上面的二进制枚举一样

Gosper’s Hack

Gosper’s Hack是一种生成 n 元集合所有 k 元子集的算法，它巧妙地利用了位运算，证明略，读者可自行查询相关资料

废话不多说，上模板

void GospersHack(int k, int n)
{int cur = (1 << k) - 1;int limit = (1 << n);while (cur < limit){int lb = cur & -cur;int r = cur + lb;cur = ((r ^ cur) >> __builtin_ctz(lb) + 2) | r;}
}

它的作用就是：在n个二进制中指定有k个1，生成所有的只含有k个1的二进制，这样可以帮助去除很多的无效二进制，同时我们可以预处理一下matrix数组，将它转化为一个二进制数组，可以优化判断

代码实现

class Solution {
public:int maximumRows(vector<vector<int>>& matrix, int numSelect) {int n = matrix.size(), m = matrix[0].size();vector<int> mask(n, 0);for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++){mask[i] += matrix[i][j] << (m - j - 1);}}int cur = (1 << numSelect) - 1, limit = 1 << m;int res = 0;while (cur <= limit) {int lb = cur & -cur;int r = cur + lb;int t = 0;for (int i = 0; i < n; i ++) {if ((mask[i] & cur) == mask[i]) ++ t;}res = max(t, res);cur = ((r ^ cur) >> __builtin_ctz(lb) + 2) | r;}return res;}
};