力扣刷题-二叉树-构建树

106.从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如，给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

思路

参考：https://www.programmercarl.com/0106.%E4%BB%8E%E4%B8%AD%E5%BA%8F%E4%B8%8E%E5%90%8E%E5%BA%8F%E9%81%8D%E5%8E%86%E5%BA%8F%E5%88%97%E6%9E%84%E9%80%A0%E4%BA%8C%E5%8F%89%E6%A0%91.html#%E6%80%9D%E8%B7%AF
首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。
流程如图：

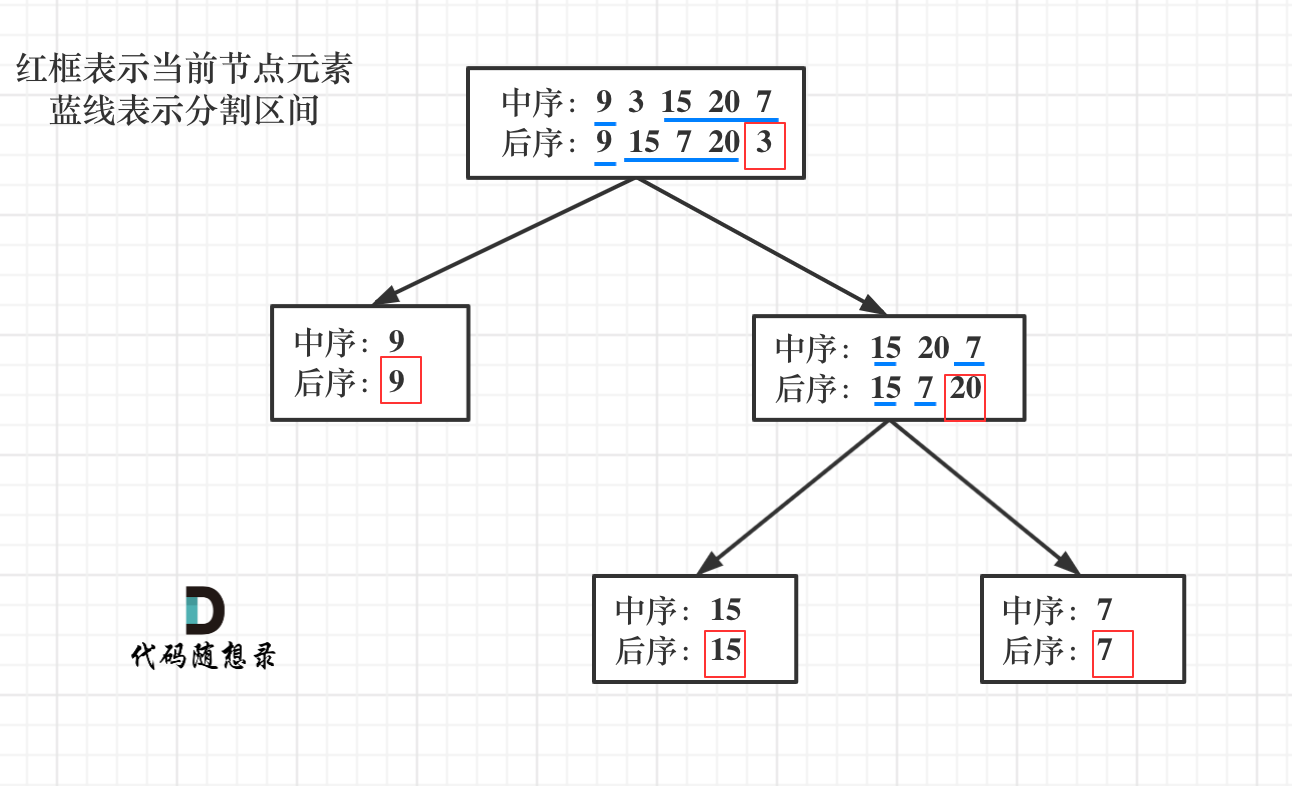
那么代码应该怎么写呢？
说到一层一层切割，就应该想到了递归。
来看一下一共分几步：
第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def buildTree(self, inorder, postorder):""":type inorder: List[int]:type postorder: List[int]:rtype: TreeNode"""# 第一步 特殊情况处理 当树为空的时候if len(inorder) == 0: # 树为空return None# 第二步 后序遍历的最后一个节点作为根节点root_val = postorder[-1] # 根节点的值root = TreeNode(root_val) # 构造根节点# 第三步 根据根节点 从中序遍历中找到分割点split_index = inorder.index(root_val) # 分割点索引# 第四步 根据分割点索引 来划分左右区间left_inorder = inorder[:split_index] # 左区间right_inorder = inorder[split_index+1:] # 右区间# 第五步 根据分割点划分 后序遍历区间 根据什么? 根据长度 因为无论是哪种遍历 左右区间的长度是一样的left_postorder = postorder[:len(left_inorder)]right_postorder = postorder[len(left_inorder):len(left_inorder)+len(right_inorder)]# 第六步 递归# 左root.left = self.buildTree(left_inorder, left_postorder)# 右root.right = self.buildTree(right_inorder, right_postorder)return root

105.从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如，给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

思路

和上面一题是一样的道理。

class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def buildTree(self, preorder, inorder):""":type preorder: List[int]:type inorder: List[int]:rtype: TreeNode"""if len(preorder) == 0:return Noneroot_val = preorder[0]root = TreeNode(root_val)split_index = inorder.index(root_val)left_inorder = inorder[:split_index]right_inorder = inorder[split_index+1:]left_preorder = preorder[1:len(left_inorder)+1]right_preorder = preorder[1+len(left_inorder):]root.left = self.buildTree(left_preorder, left_inorder)root.right = self.buildTree(right_preorder, right_inorder)return root