---

题目

统计二进制数中1的个数
输入一行，输出一行
输入： 输入一个整数
输出： 输出存储在内存中二进制的1的个数

一、方法1

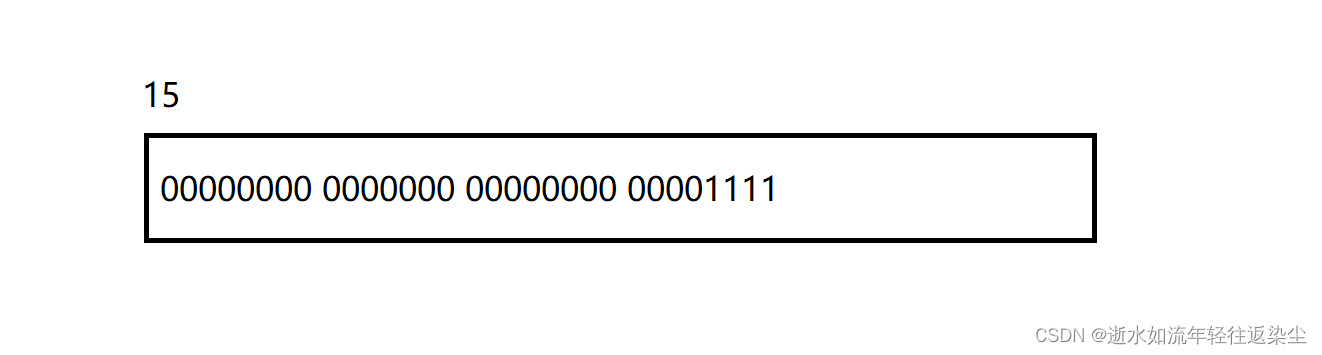
之前的文章中，小编写了有关于内存在二进制中的存储方法，正整数在二进制中存储在内存中存储的是二进制的原码，负整数在内存中存储的是二进制的补码。在这里我们随机输入一个整数，假如小编输入15，那么15在内存中存储如下图，然后我们让他按位与上一个1，在操作符中按位与语法就是两个1为1否则为0，在这里我们让15在内存中存储的二进制最低位与上1，然后二进制位右移一位让第二位与上1，因为整数在内存中存储4个字节也就是32个比特位，所以我们只需要向右移动32次就结束即可，下面上代码

int addcou(int i)
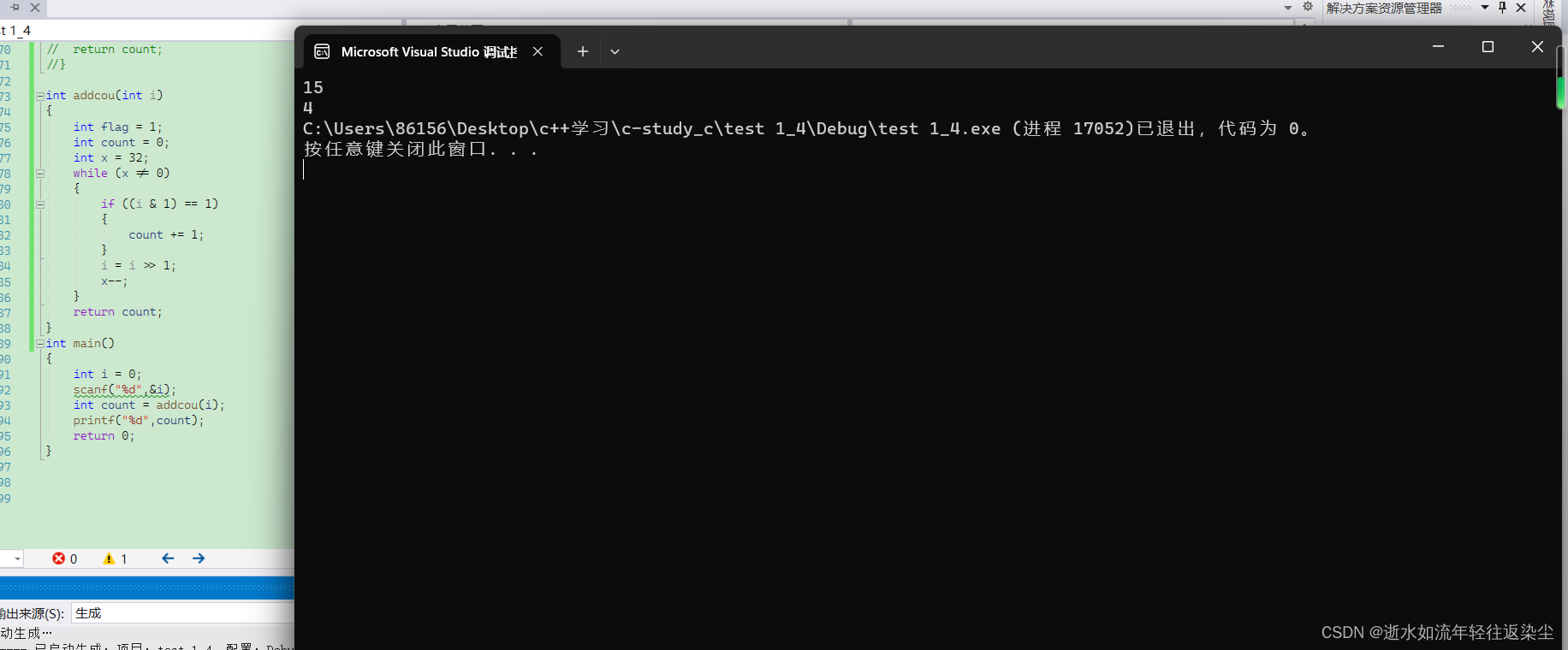
{int flag = 1;int count = 0;int x = 32;while (x != 0){if ((i & 1) == 1){count += 1;>   }i = i >> 1;   x--;   }return count;   
}
int main()   
{int i = 0;   scanf("%d",&i);   int count = addcou(i);   printf("%d",count);   return 0;   
}

二、方法2

在这里我们输入15，因为是二进制数，也就是说它的存储只有0和1，我们求它的余数要让它的范围为0和1，所以我们进来先让他取模2，在这里我们需要设置一个加数器，在这里如果取模等于1的话，计数器加1，然后再去除以2，这个也就是我们十进制转二进制数的方法，当我们最后除到最后的时候就等于0然后就没有继续换算下去，如下图，接下来上代码理解

int addcou(unsigned int i) //在这里传进来是有符号数，所以-1不够除，但是如果是无符号数，我们就会把他看成一个很大的整数这样就能求了
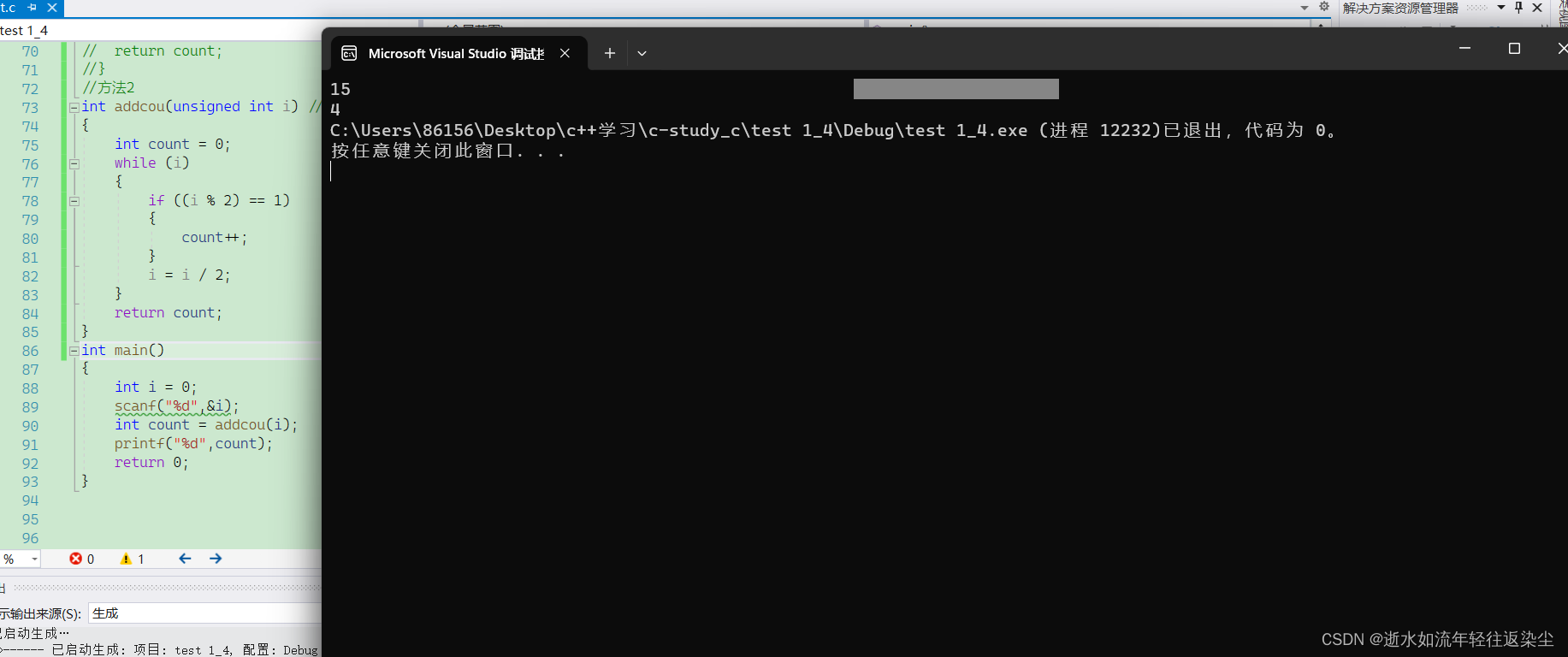
{int count = 0;while (i){if ((i % 2) == 1){count++;}i = i / 2;}return count;
}
int main()
{int i = 0;scanf("%d",&i);int count = addcou(i);printf("%d",count);return 0;
}

分析

在这里为什么传参接收用无符号整型接收呢？假如我们输入-1，而-1在内存中存储的就是它的反码，也就是32个1，但是我们如果我们直接用整型接收，因为系统默认int为有符号整型，我们这里接收-1，-1取模2不够所以得到0，然后在去除以2还是不够值所以得到-1，循环所以就是0个1，但是事实就是-1在内存中存储有32个1，因此我们用无符号整型接收，这样它就默认它二进制数也就是全是1为一个很大的整数，这样就可以统计出二进制中1的个数。

三，方法3

在这里我们接下来看到一个数假设我们输入为15，则二进制位1111，我们这里传入的是n然后让n*（n-1）

n = 15
n = n &（n-1）;
1111 n
1110 n-1
1110 n
1101 n-1
1100 n
1011 n-1
1000 n
0111 n-1
0000 n
在这里我们可以发现每次按位与一次就消去一个1，这样我们设置一个计数器，按位与一次加一然后到最后按位与为0结束，接下来上代码理解：

int addcou(int i)
{int count = 0;while (i){i = i & (i - 1);count++;}return count;
}
int main()
{int i = 0;scanf("%d",&i);int count = addcou(i);printf("%d",count);return 0;
}

---

总结

以上就是今天要讲的内容，本文仅仅简单介绍了c语言题目之统计二级制数中1的个数的使用，各位读者有其它解法欢迎打在评论区。