一 环境说明
- 群晖Nas DS418+
- DELL XPS server
- Gitlab ce
二 需要实现的功能
- 外网可以访问,gitlab
- 使用https的方式访问。
- wiki issue 等都可以上传图片和附件。
三 操作步骤
-
因为群晖上有证书,并且由群晖做转发功能。因此证书上,采用群晖的证书。获取群晖证书的步骤如下:
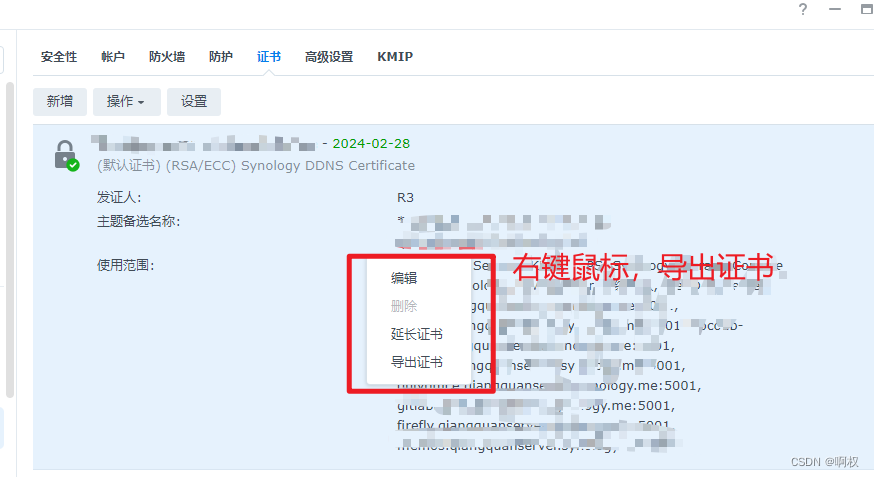
-
下载的证书解压如下:
![![[Pasted image 20240106070513.png]]](https://img-blog.csdnimg.cn/direct/c402fb3d9519439ebf964161d2ce0e58.png)
-
将以上证书移动到如下目录, /etc/gitlab/ssl, 注: ssl目录需要自己创建。
-
修改cert.pem为xxxx.crt, privkey.pem修改为xxxx.key
-
修改gitlab.rb文件
external_url 'https://域名:端口' nginx['enable'] = true nginx['client_max_body_size'] = '250m' nginx['ssl_certificate'] = "/etc/gitlab/ssl/xxxxxx.crt" nginx['ssl_certificate_key'] = "/etc/gitlab/ssl/xxxxxx.key" -
执行一下命令,重启gitlab
sudo gitlab-ctl reconfigure sudo gitlab-ctl restart -
重启完成后,测试下载代码,提交issue和WIKI贴图。目前都可以正常工作。
四 ssh下载的问题
因为目前没有使用git通过ssh的方式下载,所以暂时不做方面的测试研究。
五 备注
gitlab内网部署外网无法在WIKI上贴图的问题
之前发布的这个文章,并没有能很好的解决gitlab遇到的问题,因此,更新此文。