---

前言

如果想要判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链表，树等等数据结构都是这种思路，但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度也越来越慢 (O(n)，O(logn))。不过世界上还有一种叫作散列表（又叫哈希表，Hash table）的数据结构。它可以通过一个 Hash 函数将一个元素映射成一个位阵列（Bit array）中的一个点。这样一来，我们只要看看这个点是不是 1 就可以知道集合中有没有它了。于是乎，布隆过滤器便应运而生了。

一、概述

布隆过滤器（Bloom Filter）是 1970 年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。

主要作用：用于检索一个元素是否在一个集合中。

优点 ：

• 时间复杂度低，增加及查询元素的时间复杂度都是 O(k)，k 为 Hash 函数的个数
• 占用存储空间小，布隆过滤器相对于其他数据结构（如Set、Map）非常节省空间

缺点：

• 存在误判，只能证明一个元素一定不存在或者可能存在，返回结果是概率性的，但是可以通过调整参数来降低误判比例
• 删除困难，一个元素映射到 bit 数组上的 x 个位置为 1，删除的时候不能简单的直接置为 0，可能会影响到其他元素的判断

原理：

布隆过滤器由长度为 m 的位向量和 k个随机映射函数组成。

假设 bit array 的长度 m=10，哈希函数的个数 k=3，默认情况下 bit array 中每个坐标的值均为 0

当一个元素被加入集合时，通过多个 hash 函数计算得到多个 hash 值，以这些 hash 值作为数组的坐标，将这些坐标位置上的值设置为 1

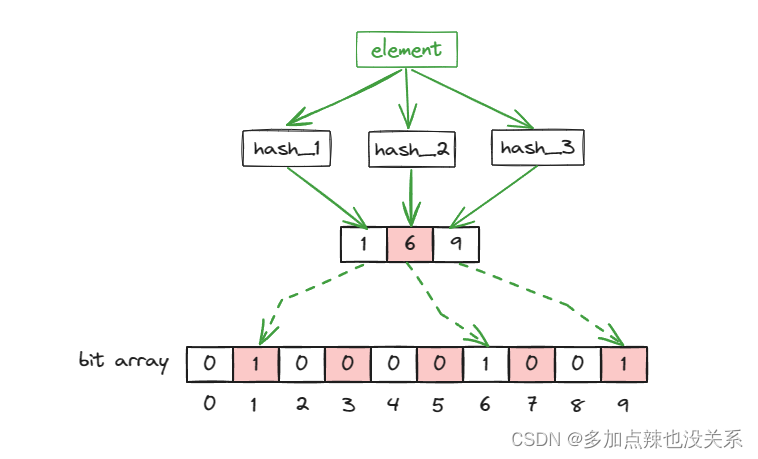
当查询该元素是否存在于集合中时，以同样的方法通过多个 hash 函数计算出对应的 hash 值，再查看这些 hash 值所对应的坐标是否均为 1，如果均为 1 则表示已存在，否则不存在

---

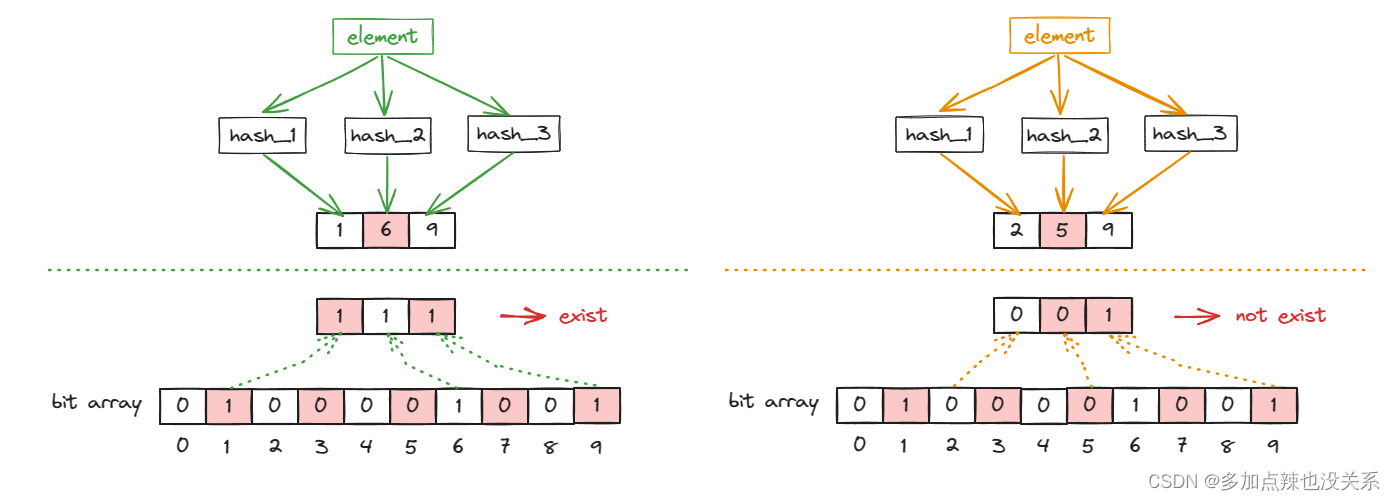
二、误差率

布隆过滤器的误差率（false positive rate）是指由于 hash 冲突，导致原本不再布隆过滤器中的数据，查询时显示在里面

哈希冲突是指当两个或多个不同的输入产生相同的哈希值时，就会发生哈希冲突

比如说有三个元素经过 k=3 个 hash 函数计算得到的哈希值分别是 [1,6,9]，[2,5,9]，[3,4,8]

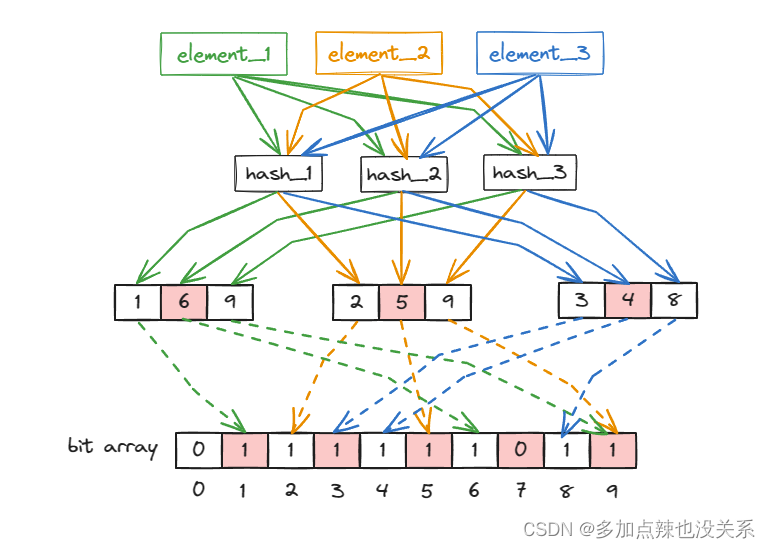
由上图可见 element_1 和 element_2 经过 hash_3 函数时得到的值均为 9，这就是 hash 冲突，虽然可能发生哈希冲突，但是由于每个元素是通过多个 hash 值来判断是否存在，所以在插入上述三个元素时均会判断出该元素不存在，此时 bit array 如下：

如果再插入第四个元素时，经过这 k=3 个 hash 函数计算后的结果是 [5,6,8]，而 5,6,8 这三个坐标在 bit array 中值均为 1，此时就会判定 element_4 已存在，实际上并没有存在，这就是布隆过滤器会存在误判的原因

随着数据量增加， bit array 中每个位置的值为 1 的比率也会增加，误判的可能性也会随之增加

那如何减少这种因为 hash 冲突而导致的误判呢？可以用公式进行推导

假设 hash 函数以等概率条件选择并设置 bit array 中的某一位，m 是该位数组的大小，k 是 hash 函数的个数，那么位数组中某一特定的位在进行元素插入时的 hash 操作中没有被置为 1 的概率是：
$$1-\frac{1}{m}$$
那么在所有 k 次 hash 操作后该位没有被置为 1 的概率是：
$$(1-\frac{1}{m}{)}^k$$
如果插入了 n 个元素，那么某一位仍然是 0 的概率是：
$$(1-\frac{1}{m}{)}^{kn}$$
因而该位为 1 的概率是：
$$1-(1-\frac{1}{m}{)}^{kn}$$
现在检测某一元素是否在该集合中，标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 1 ，但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中（误差 False Positives），该概率由以下公式确定：
$$(1-(1-\frac{1}{m}{)}^{kn}{)}^k\approx (1-e^{-kn/m}{)}^k$$

推导过程：$$(1-(1-\frac{1}{m}{)}^{kn}{)}^k=(1-(1+\frac{1}{-m}{)}^{-m\frac{-kn}{m}}{)}^k$$
由自然常数定义：$$e=\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n$$
可知，当 n 趋近于无穷大时：$$e=(1+\frac{1}{n}{)}^n$$
所以：$$(1-(1+\frac{1}{-m}{)}^{-m\frac{-kn}{m}}{)}^k=(1-e^{-kn/m}{)}^k$$
即：$$(1-(1-\frac{1}{m}{)}^{kn}{)}^k\approx (1-e^{-kn/m}{)}^k$$

由此可见，随着 m（位数组大小）的增加，误差（False Positives）的概率会下降，同时随着插入元素个数 n 的增加，误差（False Positives）的概率又会上升

对于给定的 m、n，如何选择 hash 函数个数 k？由以下公式确定：
$$k=\frac{m}{n}ln2\approx 0.7\frac{m}{n}$$

推导过程：


k 为何值时可以使得误判率最低？设误判率为 k 的函数：
$$f(k)=(1-e^{-kn/m}{)}^k$$
令：$$b=e^{\frac{n}{m}}$$
则：$$f(k)=(1-b^{-k}{)}^k$$
两边取对数：$$lnf(k)=k\cdot ln(1-b^{-k})$$
两边对 k 进行求导：
$$\frac{1}{f(k)}\cdot f^{\prime }(k)=ln(1-b^{-k})+k\cdot \frac{1}{1-b^{-k}}\cdot (-b^{-k})\cdot (-1)\cdot lnb=ln(1-b^{-k})+k\cdot \frac{b^{-k}\cdot lnb}{1-b^{-k}}$$
等式左边，常量的导数为 0，所以：$$ln(1-b^{-k})+k\cdot \frac{b^{-k}\cdot lnb}{1-b^{-k}}=0$$
$$(1-b^{-k})\cdot ln(1-b^{-k})=-k\cdot b^{-k}\cdot lnb$$
因为：$$-k\cdot lnb=ln{b}^{-k}$$
所以：$$(1-b^{-k})\cdot ln(1-b^{-k})=b^{-k}\cdot ln{b}^{-k}$$
因为， b^-k 恒小于 1，所以：$$ln(1-b^{-k})=ln{b}^{-k}$$
则等式化简为：$$1-b^{-k}=b^{-k}$$
$$b^{-k}=\frac{1}{2}$$
转化 b 得：$$e^{-\frac{kn}{m}}=\frac{1}{2}$$
$$-\frac{kn}{m}=ln2$$
则误判率最低时，得出 k 的值为：$$k=ln2\cdot \frac{m}{n}\approx 0.7\frac{m}{n}$$

此时误差（False Positives）的概率为：
$$2^{-k}\approx 0.6185^{\frac{m}{n}}$$

推导过程：

由上述推导过程可知，当：$$e^{-\frac{kn}{m}}=\frac{1}{2}$$
时函数 f(k) （即误差率）的值最小，所以：
$$f(error)=(1-e^{-kn/m}{)}^k=(1-\frac{1}{2}{)}^k=2^{-k}=2^{-ln2\cdot \frac{m}{n}}\approx 0.6185^{\frac{m}{n}}$$

而对于给定的误差（False Positives）概率 p，如何选择最优的数组大小 m 呢？
$$m=-\frac{nlnp}{(ln2{)}^2}$$

推导过程：


由上述推导过程误差率得：$$p=2^{-ln2\cdot \frac{m}{n}}$$
两边取对数：$$lnp=ln2\cdot (-ln2)\cdot \frac{m}{n}$$
则：$$m=-\frac{n\cdot lnp}{(ln2{)}^2}$$

---

三、hash 函数的选择

前面提到 hash 冲突是导致布隆过滤产生误差的主要原因，所以选择一个合适的 hash 函数是非常重要的，哈希函数的选择会影响到布隆过滤器的性能和准确性。

以下是选择哈希函数时需要考虑的一些因素：

• 均匀分布：一个好的哈希函数应该能够将输入数据均匀地分布到布隆过滤器的位数组中，以最大限度地减少碰撞的可能性
• 可扩展性：随着数据集的增加，布隆过滤器的大小也需要相应地扩展。因此，选择的哈希函数应该易于扩展，以便在增加数据集时有效地调整布隆过滤器的大小
• 稳定性：在某些情况下，如果哈希函数对输入数据的变化过于敏感，可能会导致布隆过滤器中的大量位被频繁地置为 1 或 0，这会影响布隆过滤器的性能和准确性，因此，选择一个相对稳定的哈希函数可能更为合适
• 易于实现：在选择哈希函数时，还需要考虑其实施的难易程度和可移植性。易于实现和移植的哈希函数可以减少布隆过滤器的实现和维护成本

常见的 hash 函数：

• MD5：MD5（Message Digest Algorithm 5）是一种广泛使用的密码哈希函数，它将任意长度的 “字节串” 映射为一个 128 位的大数。尽管 MD5 在许多安全应用中已经不再被视为安全的哈希函数，但在某些情况下，它仍然可以用于布隆过滤器
• SHA-1：SHA-1（Secure Hash Algorithm 1）是美国国家安全局设计，并由美国国家标准和技术研究所（NIST）发布的一系列密码散列函数。SHA-1 可以生成一个被称为消息摘要的 160 位（ 20 字节）哈希值。尽管 SHA-1 的安全性也受到一定质疑，但在某些场景下仍可用于布隆过滤器
• SHA-256：SHA-256 是 SHA-2 家族中的一种哈希函数，它生成一个 256 位（32字节）的哈希值。SHA-256 提供了比 SHA-1 更高的安全性，并且在实际应用中被广泛使用
• MurmurHash：MurmurHash 是一种非加密型哈希函数，适用于一般数据检索应用。它能够提供较好的分布性和性能，因此在布隆过滤器中也被考虑使用

---

四、手写布隆过滤器

目前 MurmurHash 函数作为布隆过滤器的 hash 函数是使用得比较多的，所以以下内容也会采用这种函数

Google Guava 库：Guava 是一个广泛使用的 Java 库，其中包含了 MurmurHash 的实现，可以使用其中的 Hashing.murmur3_128() 方法来创建 MurmurHash 实例。

<!-- guava -->
<dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>33.0.0-jre</version>
</dependency>

通过以上内容，就可以手写布隆过滤器了，代码如下：

import com.google.common.base.Charsets;
import com.google.common.hash.Hashing;
import com.mike.common.core.utils.ArithmeticUtils;import java.util.BitSet;/*** 布隆过滤器*/
public class MyBloomFilter {// 位数组，使用BitSet实现private final BitSet bits;// 位数组大小private final int bitSize;// 哈希函数的个数private final int hashFunctionCount;// 预期要存放的数据量private final int dataCount;// 期望的误判率private final double falsePositiveRate;/*** 构造方法私有*/private MyBloomFilter(int dataCount, double falsePositiveRate) {// 设置预期要存放的数据量this.dataCount = dataCount;// 实则期望的误判率（如果期望的误判率为 0，则取 double 的最小值）this.falsePositiveRate = falsePositiveRate == 0? Double.MIN_VALUE: falsePositiveRate;// 计算所需的数组大小this.bitSize = getBitSize();// 计算所需 hash 函数的个数this.hashFunctionCount = getHashFunctionCount();// 创建位数组this.bits = new BitSet(this.bitSize);}/*** 创建布隆过滤器* @param dataCount 预期要存放的数据量* @param falsePositiveRate 期望的误判率* @return 自定义布隆过滤器*/public static MyBloomFilter create(int dataCount, double falsePositiveRate) {return new MyBloomFilter(dataCount, falsePositiveRate);}/*** 获取 bit 数组的大小*/private int getBitSize() {/** 计算公式：*          m = -1 * (n*ln(p))/(ln(2)*ln(2))**          m：数组大小*          n：预估要存的数据量*          p：误判率*/return (int) (-this.dataCount * Math.log(this.falsePositiveRate) / (Math.log(2) * Math.log(2)));// 注意：Math.log(n) 就是求以自然数 e 为底 n 的对数}/*** 获取 hash 函数的数量*/private int getHashFunctionCount() {/** 计算公式：*          k = ln(2)*(m/n)**          k：hash 函数的个数*          m：bitSize 数组的大小*          n：预估要存的数据量*/return Math.max(1, (int) Math.round((double) this.bitSize / this.dataCount * Math.log(2)));}/*** 往布隆过滤器中添加数据* @param data 数据* @return 结果：true 表示插入成功，false 表示插入失败*/public boolean add(String data) {// 先假设插入失败boolean insert = false;// 计算 hash 值long murmurHash = Hashing.murmur3_128().hashString(data, Charsets.UTF_8).asLong();int hash1 = (int)murmurHash;int hash2 = (int)(murmurHash >>> 32);for (int i = 1; i <= hashFunctionCount; i++) {// 通过 murmurHash 与哈希函数个数的序号得到一个新的 hash 值int hash = hash1 + i * hash2;if (hash < 0) {// 如果 hash 小于 0，则进行取反操作hash =~hash;}// 获取更新为 1 的数组坐标位置（取 % 可以让得到的数不超过数组的大小）int index = hash % bitSize;// 通过该坐标值判定该位置是否已被设置为 1boolean exist = bits.get(index);if (!exist) {// 未已设置过则进行更新bits.set(index, true);// 设置已插入insert = true;}}return insert;}/*** 检查数据是否存在*/public boolean exist(String data) {// 逻辑和 add 方法类似long murmurHash = Hashing.murmur3_128().hashString(data, Charsets.UTF_8).asLong();int hash1 = (int)murmurHash;int hash2 = (int)(murmurHash >>> 32);for (int i = 1; i <= this.hashFunctionCount; i++) {int hash = hash1 + i * hash2;if (hash < 0) {hash =~hash;}int index = hash % bitSize;if (!bits.get(index)) {// 有一个数组位上没有被设置过，则表示不存在return false;}}return true;}
}

测试代码：

public class BloomFilterDemo {public static void main(String[] args) {// 预期存放十万个数据int dataCount = 1000000;// 预期误差率为 0.01double falsePositiveRate = 0.01;// 创建布隆过滤器MyBloomFilter bloomFilter = MyBloomFilter.create(dataCount, falsePositiveRate);// 添加数据for (int i = 0; i < dataCount; i++) {String data = String.valueOf(i);bloomFilter.add(data);}// 添加从 dataCount 起后 100000 个数据int falsePositiveCount = 0;for (int i = dataCount; i < dataCount+100000; i++) {String data = String.valueOf(i);if (bloomFilter.exist(data)) {// 如果判断存在，则表示误判了，统计falsePositiveCount++;}}System.out.println("误差个数：" + falsePositiveCount);}
}

运行 main() 方法，控制台信息如下：

可以看到误差率也是接近前面预设的 0.01%

---

五、guava 中的布隆过滤器

上面内容我们通过布隆过滤器的原理和一些推导公式，实现了布隆过滤器，不过一般也不会自己去手写布隆过滤器，因为有些包中已经实现了布隆过滤器，比如： guava

在前面布隆过滤器的实现中，有些代码我也是参考了 guava 中的 BloomFilter 去实现的

那如何使用 guava 给的布隆过滤器呢？

导入 guava 依赖（就是第四部分导入的依赖）：

<!-- guava -->
<dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>33.0.0-jre</version>
</dependency>

我们可以使用 BloomFilter 中的 create() 方法来创造布隆过滤器

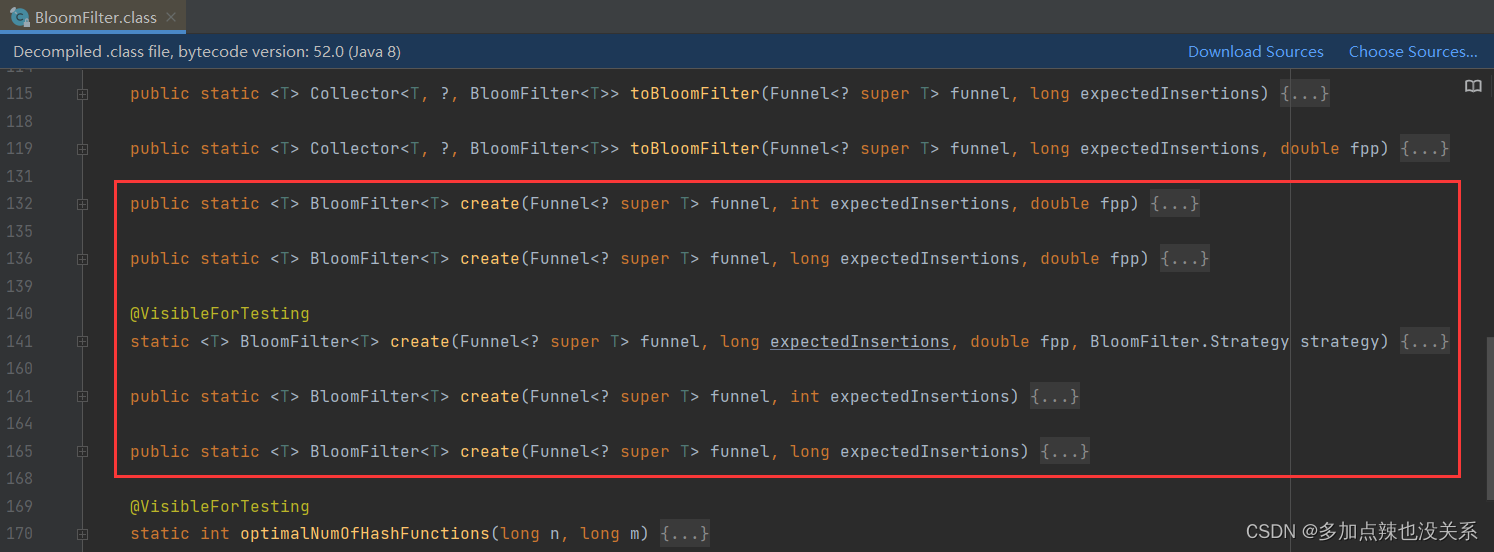
比如：创建一个针对存储字符串类型的布隆过滤器

        // 创建布隆过滤器BloomFilter<String> bloomFilter = BloomFilter.create(// 过滤器只存储字符串类型的数据，字符集为 uft-8Funnels.stringFunnel(Charsets.UTF_8),// 预期存放数据量dataCount, // 预期误差率falsePositiveRate);

使用 put() 方法添加元素，mightContain() 方法判断元素是否存在

上述测试代码用 guava 的布隆过滤器可改写为：

package com.mike.spider;import com.google.common.base.Charsets;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;public class BloomFilterDemo {public static void main(String[] args) {// 预期存放十万个数据int dataCount = 1000000;// 预期误差率为 0.01double falsePositiveRate = 0.01;// 创建布隆过滤器BloomFilter<String> bloomFilter = BloomFilter.create(// 过滤器只存储字符串类型的数据，字符集为 uft-8Funnels.stringFunnel(Charsets.UTF_8),// 预期存放数据量dataCount,// 预期误差率falsePositiveRate);// 添加数据for (int i = 0; i < dataCount; i++) {String data = String.valueOf(i);bloomFilter.put(data);}// 添加从 dataCount 起后 100000 个数据int falsePositiveCount = 0;for (int i = dataCount; i < dataCount+100000; i++) {String data = String.valueOf(i);if (bloomFilter.mightContain(data)) {// 如果判断存在，则表示误判了，统计falsePositiveCount++;}}System.out.println("误差个数：" + falsePositiveCount);}
}

---

参考文章：

Java实现布隆过滤器的几种方式：https://blog.csdn.net/weixin_43888891/article/details/131407465

布隆过滤器(一)：https://hardcore.feishu.cn/docs/doccntUpTrWmCkbfK1cITbpy5qc

布隆过滤器（Bloom Filter）- 原理、实现和推导：https://blog.csdn.net/hlzgood/article/details/109847282

布隆过滤器讲解及基于Guava BloomFilter案例：https://blog.csdn.net/weixin_42675423/article/details/130025590