数据结构之单调栈、单调队列

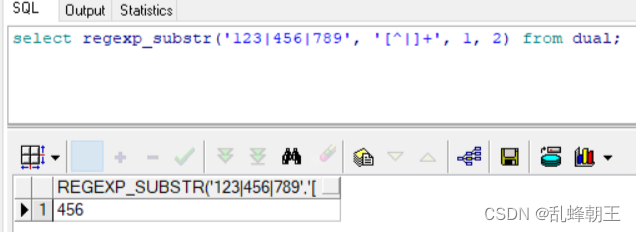
今天学习了单调栈还有单调队列的概念和使用，接下来我将对其定义并配合几道习题进行讲解：

首先先来复习一下栈与队列：

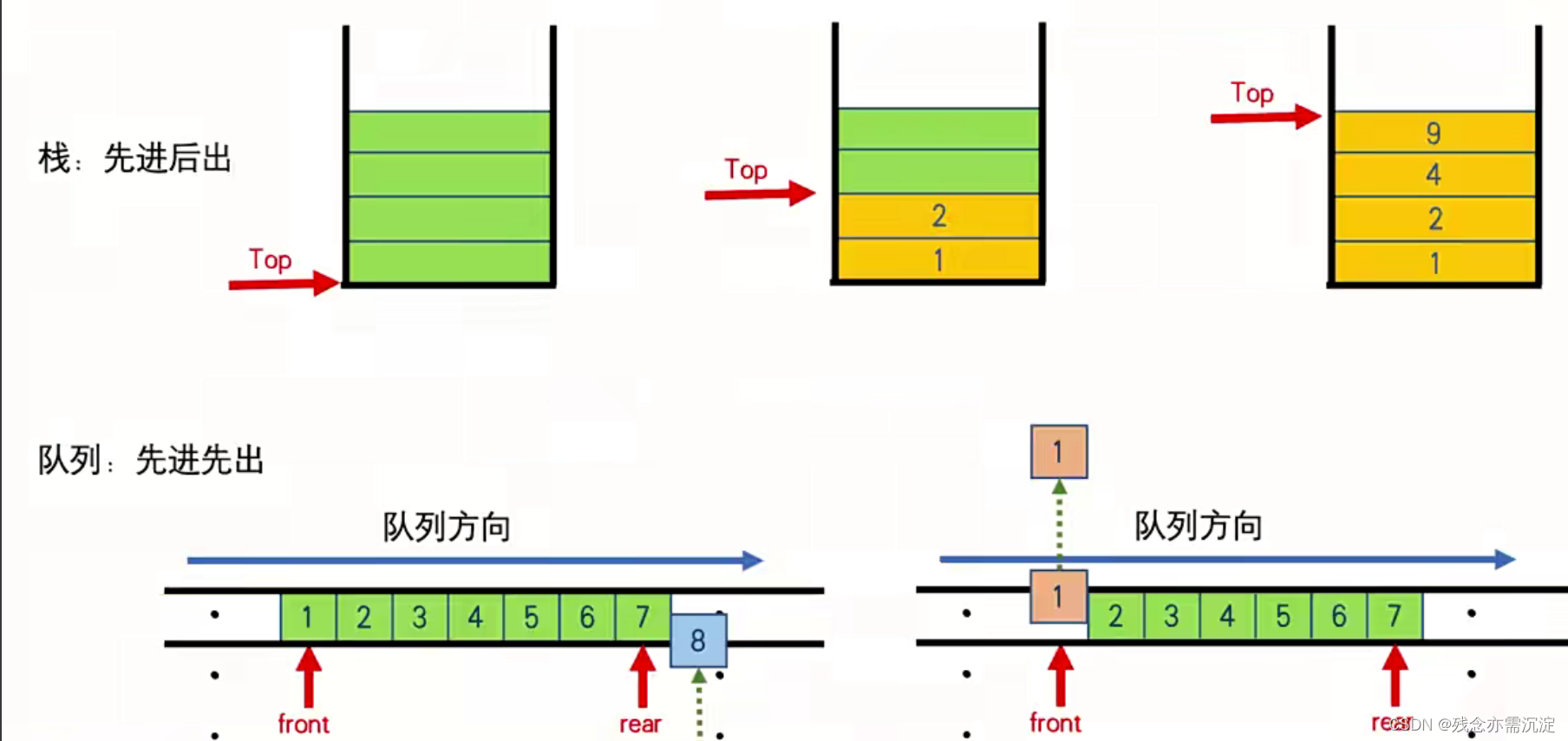
然后我们来看一下单调栈的定义：
单调栈中的元素从栈底到栈顶的元素的大小是按照单调递增或者单调递减的关系进行排列的，由于它的这个性质可以方便我们解决很多问题，接下来看一道可以用这个单调栈来解决的例题：

接下来我会提供两个不同的代码但其实本质一样的解答，我们可以用样例模拟一下过程，这里我们考虑用一个单调递减的栈进行解答：

首先2进栈，然后接下来是6进栈，首先我们判断出6比2大，那么2对应的答案就是6的下标2并将2出栈，接下来3 1依次进栈，他们两个都满足递减，接下来5进栈之后，5对应的下标就是3 1两个的答案，并将这两个出栈，这样一直模拟下去就会得到每一个的答案，接下来上代码（从左往右看）：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int a[N],top,ans[N],n,s[N];
int main(){//先完成所有的输入cin>>n;for(int i=1;i<=n;i++)cin>>a[i];//这里就是本题的模拟过程for(int i=1;i<=n;i++){//我们这个时候栈即将进来一个元素，这时候我们将这个元素与单调递减栈中元素从上往下进行比较while(top && a[i]>a[s[top]]){//如果满足while循环条件，也就是即将进站元素大于栈顶元素，那么栈顶元素对应的答案下标就是即将进栈元素的下标ans[s[top]]=i;//将栈顶元素出栈--top;}//将这个元素进栈s[++top]=i;}//最后由于会有后面不存在比他更大的元素，这时候把他们都设置为0for(int i=1;i<=top;i++)ans[s[i]]=0;//逐个输出for(int i=1;i<=n;i++)cout<<ans[i]<<' ';return 0;
}

上面的代码我附着了详细的讲解

这里其实也可以从右往左进行枚举并同样使用单调栈进行解答，代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n,top,a[N],s[N],ans[N];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];//从右往左进行模拟for(int i=n;i;i--){//当栈非空并且栈顶元素是小于即将进栈的元素时将栈顶元素去除while(top && a[s[top]]<=a[i])--top;//如果栈非空，则说明这时候栈顶元素就是大于此时即将进栈元素的第一个元素if(top) ans[i]=s[top];else ans[i]=0;//否则就没有比他更大的数s[++top]=i;//入栈}//逐个输出for(int i=1;i<=n;i++)cout<<ans[i]<<' ';return 0;
}

接下来看第二道题目：

最大矩形面积：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int a[N],top,l[N],r[N],n,s[N];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];//从左往右计算每个位置左边第一个比他矮的for(int i=1;i<=n;i++){while(top && a[i]<=a[s[top]])--top;if(top) l[i]=s[top];else l[i]=0;s[++top]=i;}//清空栈top=0;//从右往左模拟计算每个数字右边第一个高度小于它的位置for(int i=n;i;i--){if(top && a[i]<=a[s[top]])	--top;if(top) r[i]=s[top];else r[i]=n+1;//入栈s[++top]=i;}long long ans=0;//计算最大的矩形面积for(int i=1;i<=n;i++)ans=max(ans,1LL*a[i]*(r[i]-l[i]-1));cout<<ans<<endl;return 0;
}

第三题的难度较大：数对统计

接下来我会给出代码并附着具体的思路以及分析：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n;
int a[N],s[N],top,ans;
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];/*上面是输入部分*//*接下来我们分析一下题目 题目共有n个不同的数字，我们要求出有多少个数对i，j在i，j中之间的元素不存在大于边界的元素的数对个数我们可以分析首先挨着的两个数字都能达到这样的条件，因为他俩之间一个数字都没有然后我们考虑当有三个及以上数字的数对的时候，中间的所有元素都不能大于两边，这里就是我们运用单调栈解答的关键思路*/for(int i=1;i<=n;i++){/*下标为i的元素即将进栈*/while(top && a[i]>=s[top]){/*将即将进栈的元素与栈顶元素作大小的对比如果大于栈顶元素，那么以栈顶元素开始的数对i，满足条件的j的数对的终点最长也就是此时即将进栈的元素，因此移除栈顶元素并让答案加一*/--top;++ans;}if(top) ++ans;//这里如果栈顶还有元素的话，说明这个栈顶的元素是大于即将进栈的元素的，那么他们之间的所有元素与以栈顶元素还有即将进栈的元素组成的数对满足条件s[++top]=a[i];/*上述for循环中 我们考虑的是运用一个单调栈来模拟一个答案数量的增加过程*/cout<<ans<<endl;//输出答案return 0; 
}

接下来看单调队列：

定义：队列中的元素按照递增或者递减的线性关系排列的队列。

利用队列先进先出的特点以及单调队列的特质可以用来解决很多的问题，接下来看例题：

1.动态区间的最大数：

这个题目我们考虑用一个单调递减的队列进行解答：

我们可以维护队首元素是最大的数字，他就是每个m长度区间的答案，然而他最多只可能连续被输出m次，因为无论多大，队列的长度最大同时只能是m，总的来说我们需考虑下面三个问题：

接下来上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n,m;
int a[N],q[N],front=1,rear=0;
int main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];/*接下来是代码的精华部分*/for(int i=1;i<=n;i++){while(front<=rear && a[q[rear]]<=a[i])//当队列非空并且即将入队的元素是大于队尾元素的时候--rear;	//由于要维护一个单调递减的队列，所以这个时候需要将队尾元素暂时性出队q[++rear]=i;//将对应的元素下标入队/*这里想说明一点就是当前子队列的下标是从front开始到i的，虽然中间会更换队尾的元素以便于维护单调队列的单调性，但是右边界始终就是i*/if(m<i-q[front]+1) ++front;//当队列的长度大于m的时候，将队首元素出队,这时候的最大值应该是后面队列中进行挑选了if(i>=m) cout<<a[q[front]]<<' ';//输出每个对应的动态区间的最大值}return 0;
}

接下来看这道题的模板：

接下来看第二道例题：

接下来附上代码以及讲解：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n,m,a[N],s[N],q[N],front=1,rear=0,l,r;
int main(){cin>>n>>l>>r;s[0]=0;for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]+a[i];}// 上面完成所有的输入并且利用s数组来计算出所有的前缀和int x=l,ans=-1<<30;//将x的长度初始值设置成为最短的区间长度l并且由于a数组中的元素可能都为负数那么我们一开始的默认ans需要设置的很小以便于应付极端情况这里的x其实也就是区间的右端点//接下来从1开始进行枚举并通过维护一个单调递减的队列，其中存储的是前缀和数组的下标for(int i=1;i+l-1<=n;i++){//请注意这里的i其实是区间和的左端点，队列中我们存储的都是前缀和数组的下标while(x<=i+r-1 && x<=n){//这个x是用来维护一个长度为l到r的并且小于数组长度n的一个区间长度while(front <= rear && s[q[rear]]<=s[x])//当队列非空的时候为了维护一个单调递减的前缀和区间队列，进行队列的更新--rear;q[++rear]=x;//将x插入到队尾++x;//并且将x的长度加一}if(q[front]<i+l-1)//当这时候队首对应的前缀和区间长度不足l的时候，将队首出队++front;ans=max(ans,s[q[front]]-s[i-1]);//更新最大的ans}cout<<ans<<endl;return 0; 
}

这一道题目需要仔细的理解单调队列在其中的运用，请读者仔细领悟与思考。

接下来看最后一道题目，覆盖：

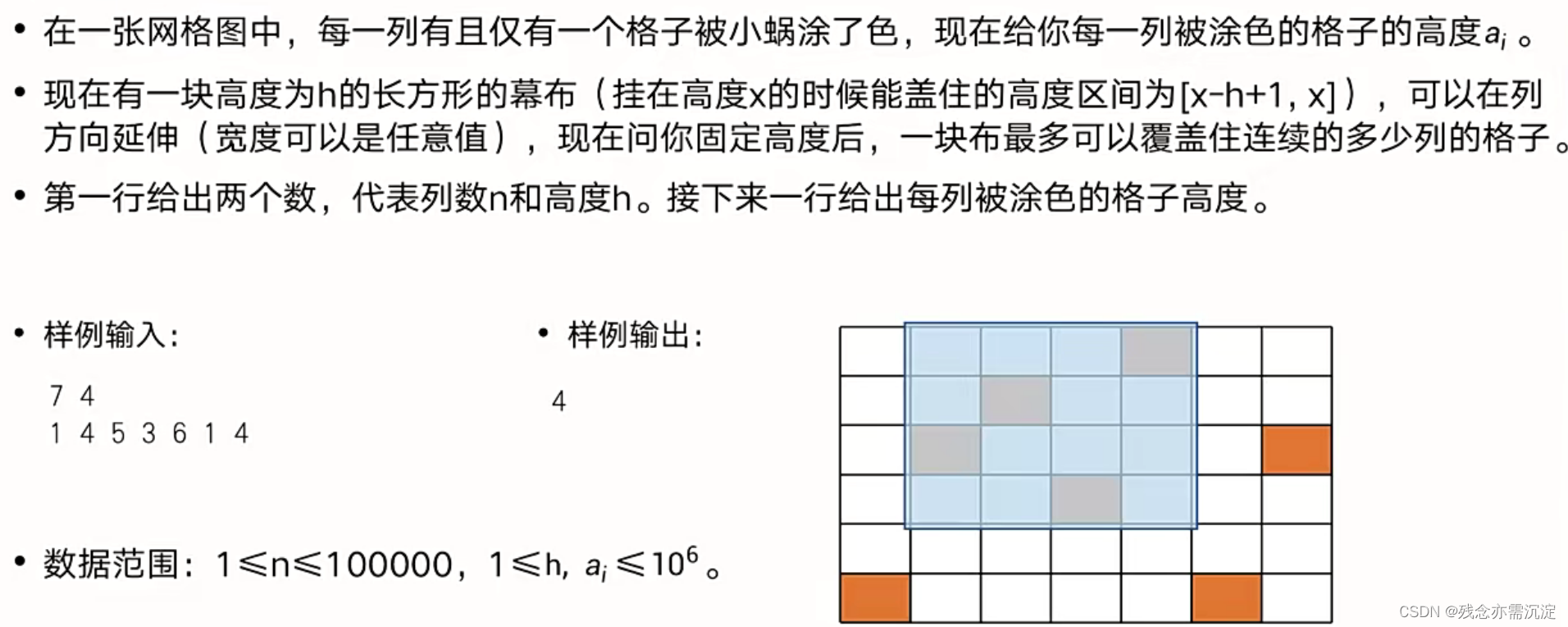
接下来请看代码：

#include <bits/stdc++.h>using namespace std;int n, h, a[200001], q1[200001], front1 = 1, rear1 = 0, q2[200001], front2 = 1, rear2 = 0; int main() {scanf("%d%d", &n, &h);for (int i = 1; i <= n; i++)scanf("%d", &a[i]);int j = 0, ans = 0;for (int i = 1; i <= n; i++) {if (front1 <= rear1 && q1[front1] < i)++front1;if (front2 <= rear2 && q2[front2] < i)++front2;while (j <= n && (j <= i || a[q1[front1]] - a[q2[front2]] <= h)) {++j;if (j > n)break;while (front1 <= rear1 && a[q1[rear1]] <= a[j])--rear1;q1[++rear1] = j;while (front2 <= rear2 && a[q2[rear2]] >= a[j])--rear2;q2[++rear2] = j;}ans = max(ans, j - i);}printf("%d\n", ans);
}

数组初始化：
- a[200001]：存储输入的 n 个数字。
两个单调队列：
- q1：维护最大值的单调递减队列。
- q2：维护最小值的单调递增队列。
- front1、rear1、front2、rear2：队列的头尾指针。
主要逻辑：
- 通过双指针 i 和 j 遍历数组。
- 对于每个位置 i，在内循环中找到满足条件的 j，使得子序列中最大值和最小值的差值不超过 h。
- 在 j 的移动过程中，更新两个单调队列 q1 和 q2。
- 计算并更新最大长度 ans。
内循环：
- 在 j 的循环中，不断尝试扩展子序列的右边界 j，直到满足条件：a[q1[front1]] - a[q2[front2]] <= h 或者超出数组范围。
- 更新两个队列 q1 和 q2 以维护最大值和最小值的索引。
最终结果：
- 输出得到的最大长度 ans，即符合条件的连续子序列的最大长度。