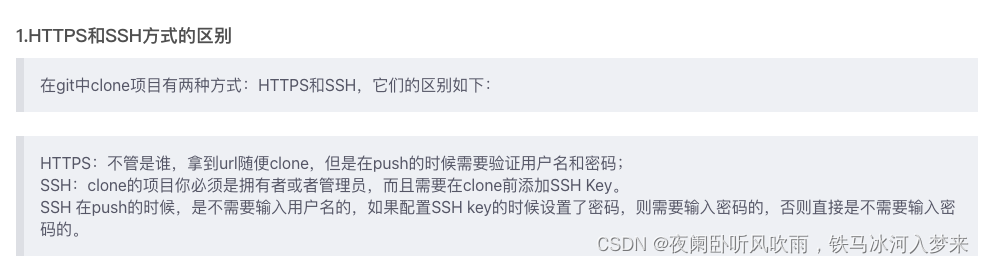
典型相关分析(Canonical Correlation analysis)
研究两组变量(每组变量中都可能有多个指标)之间相关关系的一种多元统计方法。它能够揭示出两组变量之间的内在联系。
注:本文源于数学建模学习交流相关公众号观看学习视频后所作
目录
例子引入
解决思路
代表性变量如何选择
典型相关分析
定义
思路
关键步骤
Spss操作步骤
(1)导入数据
(2)检验数据的类型
(3)点击菜单功能
(4)将数据移动到对应的集合
(5)导出分析结果
(6)对结果进行分析
例子引入
我们要探究观众和业内人士对于一些电视节目的观点有什么样的关系呢?
观众评分来自低学历(led)、高学历(hed)和网络(net)调查三种,它们形成第一组变量。而业内人士分评分来自包括演员和导演在内的艺术家(arti)、发行(com)与业内各部门主管(man)三种,形成第二组变量。
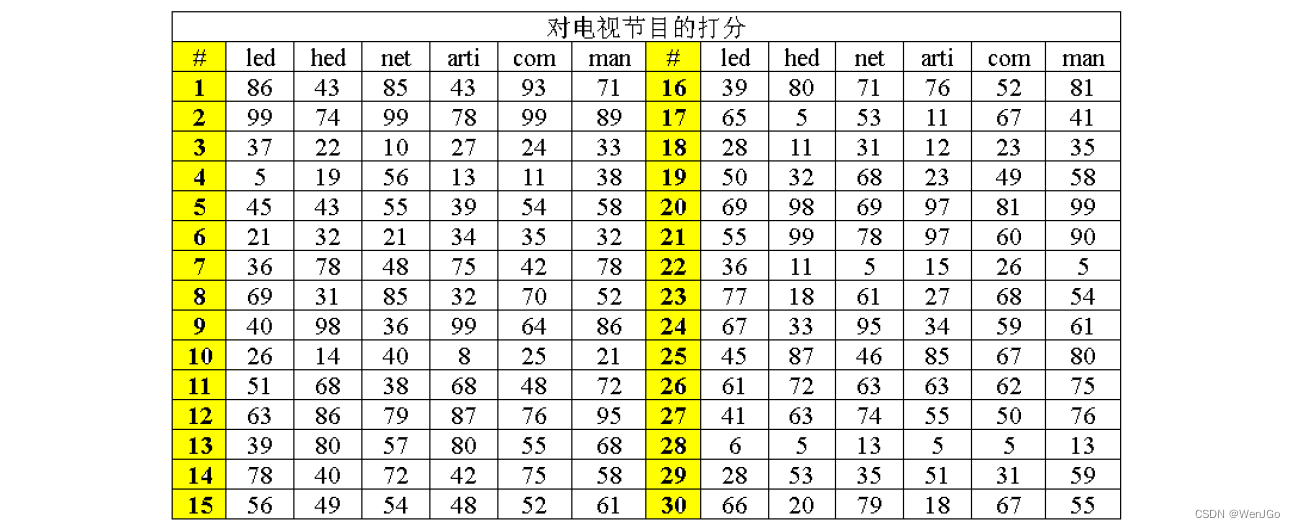
案例来源:人大吴喜之《从数据到结论》
可以发现直接对这些变量的相关进行两两分析,很难得到关于这两组变量(观众和业内人士)之间关系的一个清楚的印象。
解决思路
把多个变量与多个变量之间的相关,化为两个具有代表性的变量之间的相关。
代表性变量如何选择
代表:能较为综合、全面的衡量所在组的内在规律。
一组变量最简单的综合形式就是该组变量的线性组合。
典型相关分析
定义
典型相关分析由Hotelling提出,其基本思想和主成分分析非常相似。
(1)首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数;
(2)然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对;
(3)如此继续下去,直到两组变量之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。
思路

详细证明我上传了一个文件,厦门大学多元统计分析第九章典型相关分析.ppt
关键步骤
(1)数据的分布有假设:两组数据服从联合正态分布。

(2)首先要对两组变量的相关性进行检验(构造似然比统计量)。
p 值 < 0.05(0.1)表示在 95%(90%)的置信水平下拒绝原假设,即认为两组变量有关。

(3)确定典型相关变量的个数(直接看典型相关系数对应的P值即可)

(4)利用标准化后的典型相关变量分析问题

(5)进行典型载荷分析
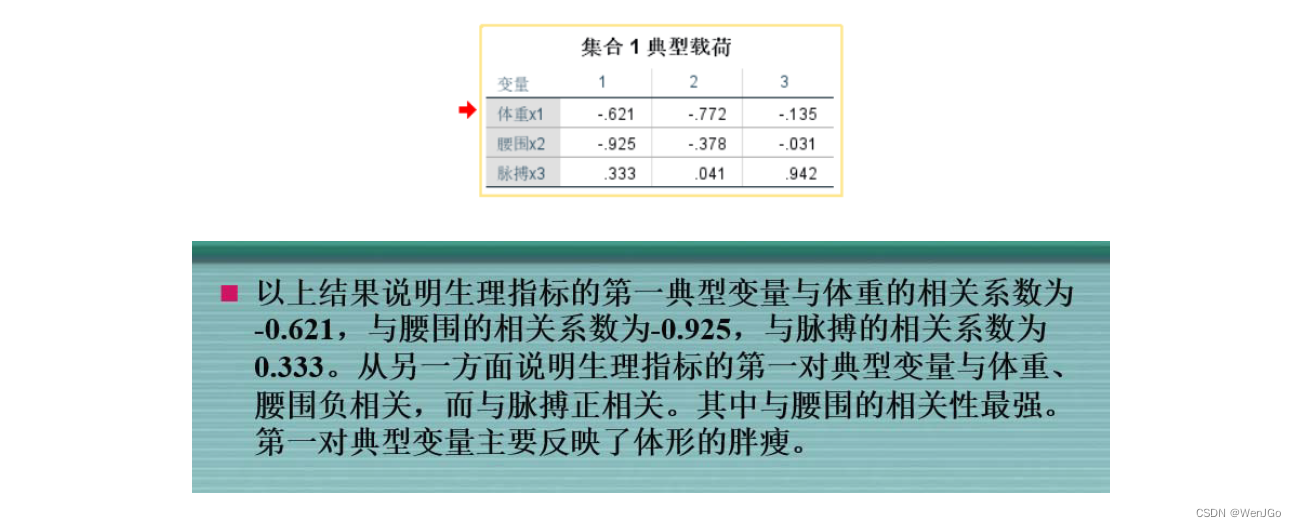
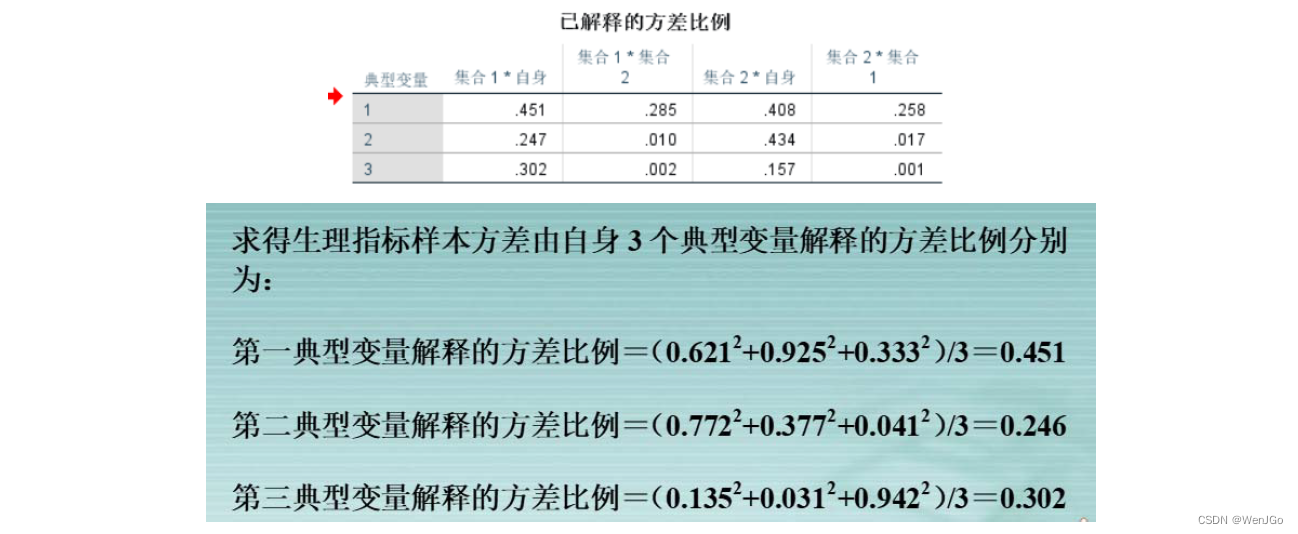
(6)计算前r个典型变量对样本总方差的贡献
Spss操作步骤
注意:Spss至少需要24版本,低版本不能直接进行典型相关分析的操作,需要编程。(如果新版本仍不能运行,则检查电脑用户名是否为中文,如果是中文的话就需要在电脑上新建一个用户,在新用户上面重新安装SPSS)
(1)导入数据

(2)检验数据的类型
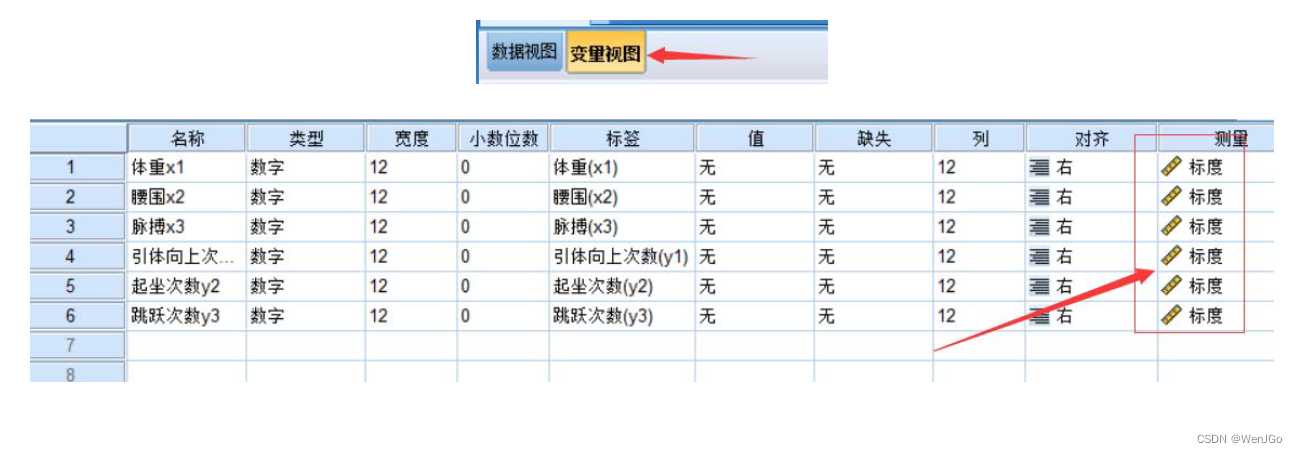
全部设置为标度
(3)点击菜单功能
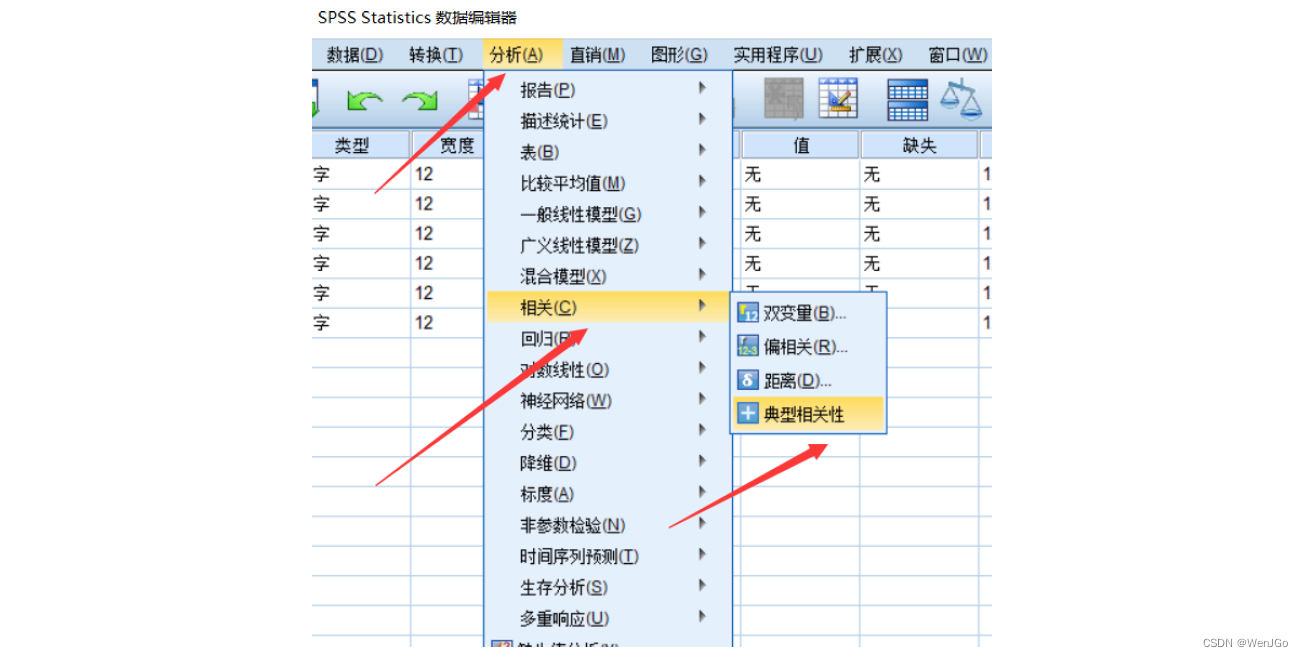
(4)将数据移动到对应的集合

(5)导出分析结果
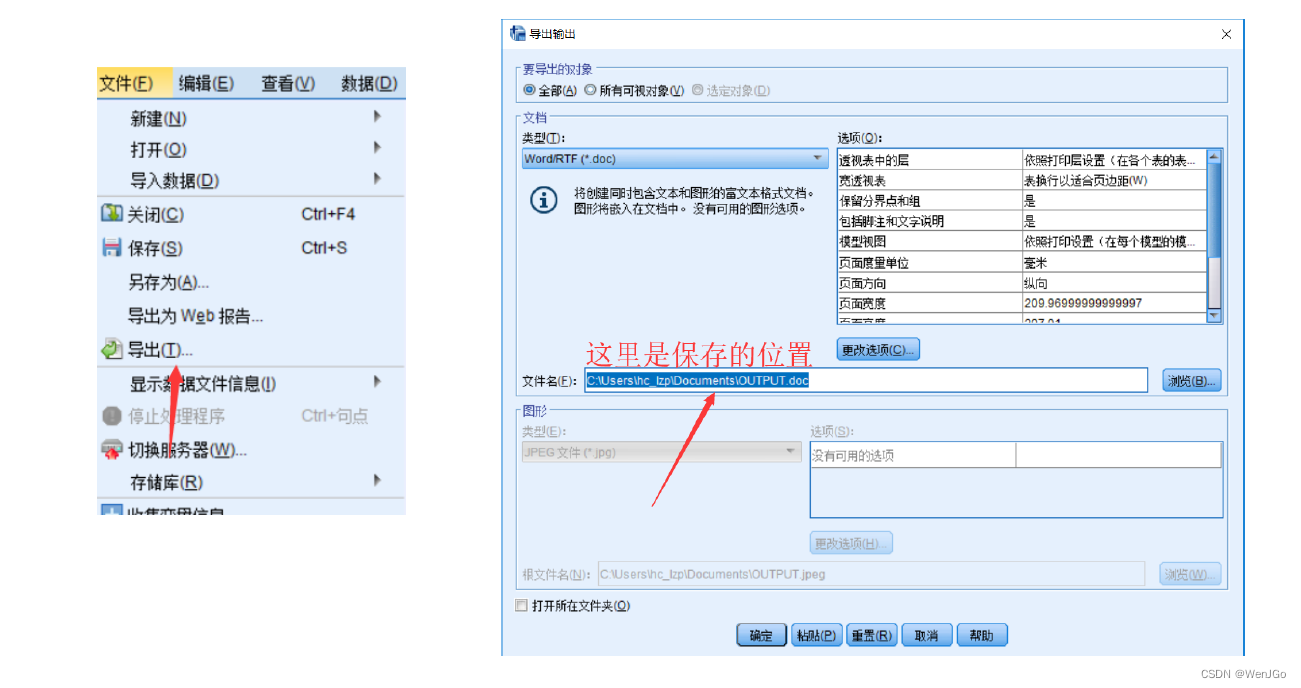
(6)对结果进行分析
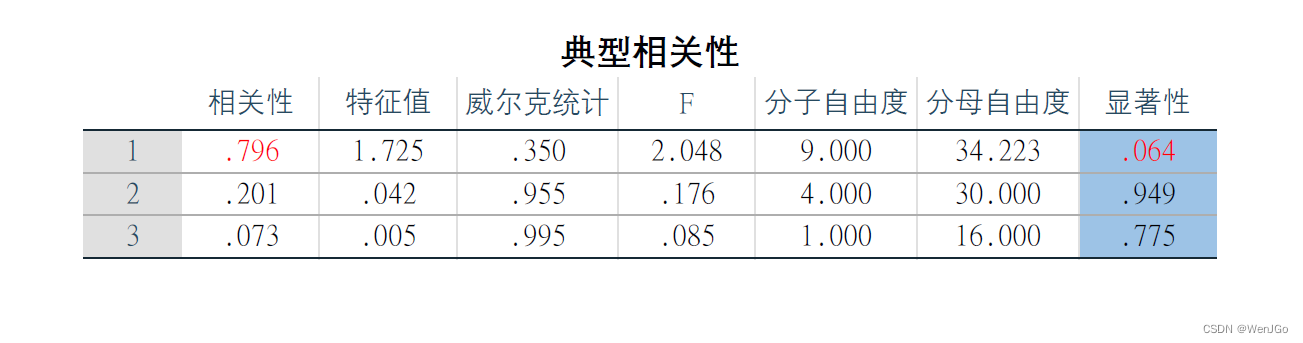
首先看这张表格的最后一列,这一列代表着检验统计量所对应的p值,我们要通过它确定典型相关系数的个数。

写出标准化后的典型变量
(根据上一步确定个数来写,有几个显著的典型相关性系数就要写几对出来)



典型变量每个分量前面的系数代表着重要程度,可结合典型相关系数进行分析。
后面选择性的分析典型载荷和方差解释程度。

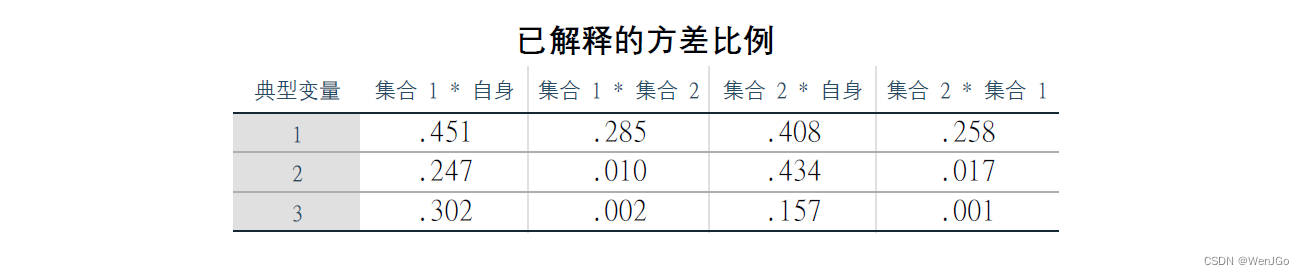
结语
结束,┏(^0^)┛