目录
一、堆的定义
1、堆的定义:
2、根节点与其左、右孩子间的联系
二、堆的创建
1、堆的向下调整算法
2、堆的向上调整算法
三、堆排序
一、堆的定义
1、堆的定义:
堆可以被看作是一棵完全二叉树的数组对象。即在存储结构上是数组,在逻辑结构上是一棵完全二叉树。在堆中,树的每个节点都满足堆属性,即父节点的值大于(或小于)其子节点的值。
具体而言,对于最大堆,父节点的值大于等于其子节点的值;而对于最小堆,则是父节点的值小于等于其子节点的值。这使得堆的根节点(常常是数组的第一个元素)成为堆中最大(或最小)的元素。
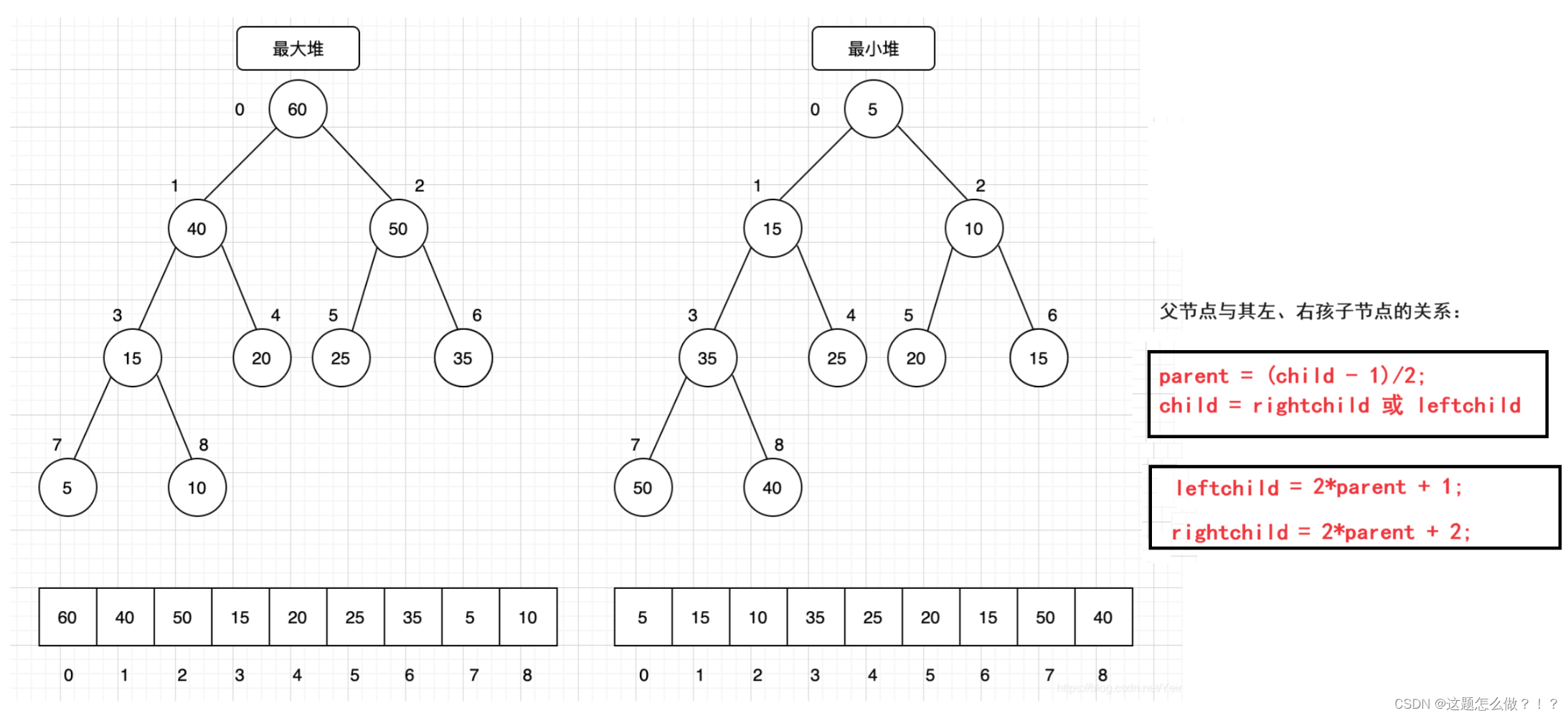
2、根节点与其左、右孩子间的联系
在堆中,根节点和其子节点之间存在一种特殊的联系。
对于任意一个节点 i,其左子节点位于位置 2i+1,右子节点位于位置 2i+2。反之,对于任意一个节点 j,其父节点位于位置 (j-1)/2。(这里的位置是指在数组中的索引位置)
换句话说,如果我们将堆表示为一个数组,那么对于任意节点 i,其左子节点就是数组中下标为 2i+1 的元素,右子节点就是数组中下标为 2i+2 的元素。而节点 i 的父节点就是数组中下标为 (i-1)/2 的元素。
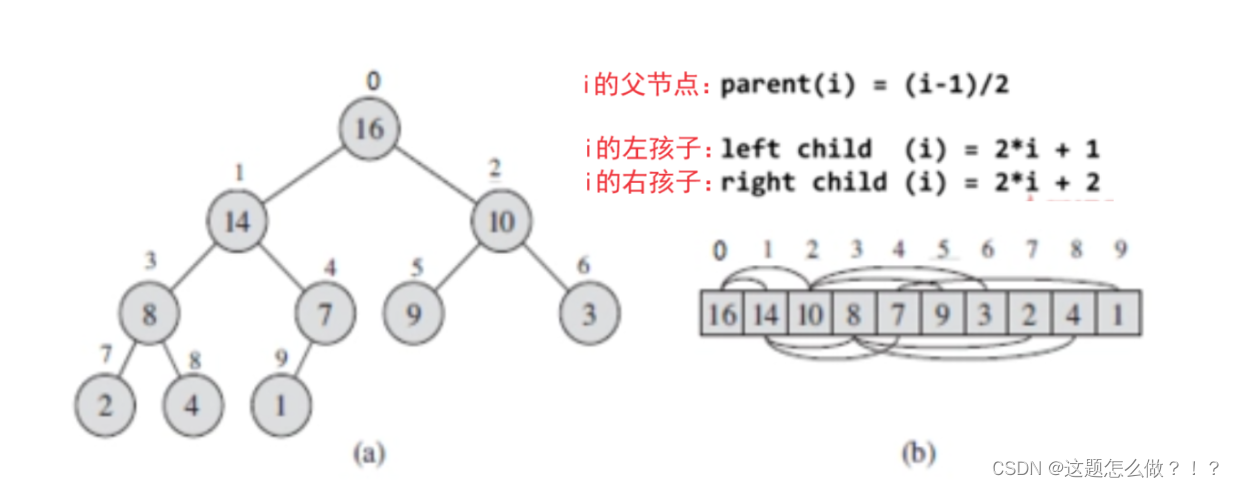
二、堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们介绍两种方法:堆的向下调整算法和堆的向上调整算法
1、堆的向下调整算法
这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
具体步骤如下:
-
首先,根据二叉树的性质,最后一个非叶子节点的索引可以通过
(n-2)/2计算得到,其中n是二叉树的节点总数。 -
我们可以使用一个循环,从最后一个非叶子节点开始,依次向前遍历每个节点。
-
对于每个节点,我们可以调用
AdjustDown函数来对其进行向下调整的操作。 -
通过依次向上调整每个节点,我们可以确保整个二叉树满足堆的性质。

代码及注释:
#include <stdio.h>
#include<stdlib.h>void swap(int* a, int* b)
{int temp;temp = *a;*a = *b;*b = temp;
}void AdjustDown(int* a, int n, int root)
{int child; // 子节点的索引child = root * 2 + 1; // 计算左孩子节点的索引while (child < n) // 当存在孩子节点时循环{if (child + 1 < n && a[child + 1] > a[child]) // 如果存在右孩子且右孩子大于左孩子{child++; // 将 child 置为右孩子的索引}if (a[root] < a[child]) // 如果根节点小于孩子节点{swap(&a[root], &a[child]); // 交换根节点和孩子节点的值}root = child; // 将根节点更新为孩子节点child = root * 2 + 1; // 计算新根节点的左孩子节点索引}
}int main()
{int a[] = {10,1,3,2,4,6,8,9,7};int n = sizeof(a) / sizeof(int);int root = (n - 2) / 2;int i;for (i = root; i >= 0; i--){AdjustDown(a, n, i); // 对每个根节点进行向下调整操作}for (i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
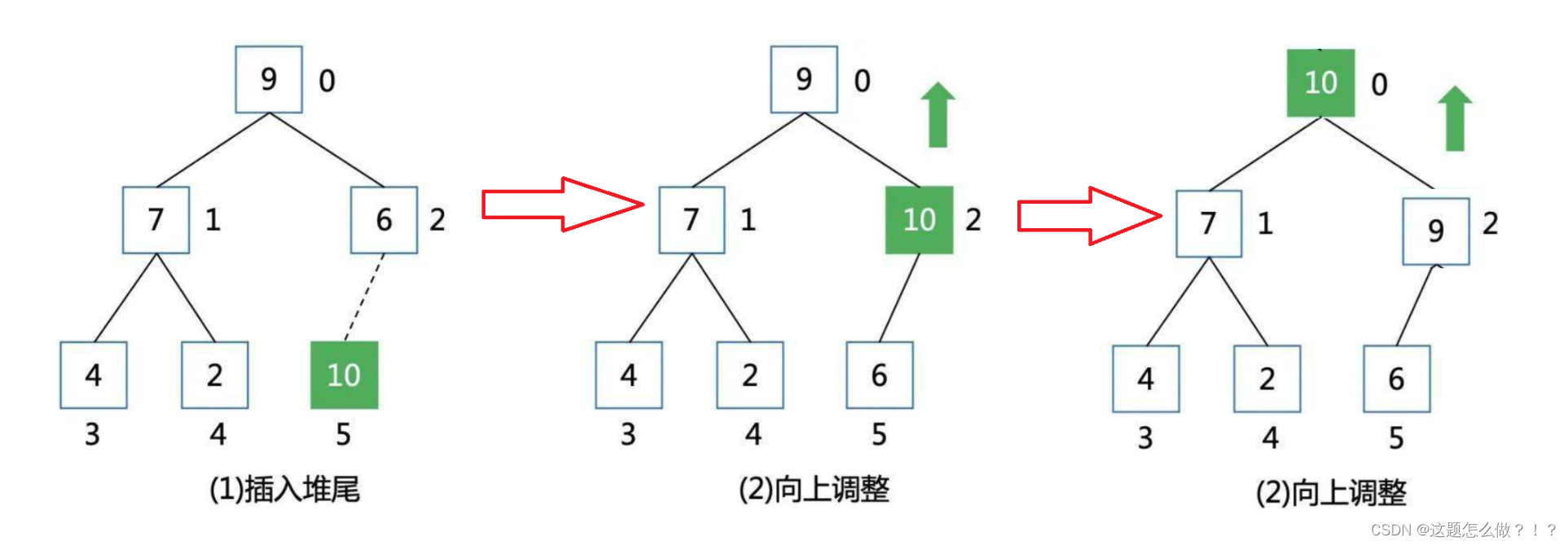
}2、堆的向上调整算法
- 开始时,我们将数组第一个元素视为一个堆。
- 对于后续每个元素,调用
AdjustUp函数进行向上调整的操作,使当前包含的数组元素满足堆的性质——即向堆中插入数据并通过向上调整使其成为新的堆。 AdjustUp函数比较元素的值与其父节点的值,如果子节点的值大于父节点的值,则交换两个节点的值,并把child更新为其父节点的索引,继续向上比较。- 这样循环调整每个元素,可以使整个数组满足堆的性质。
代码及注释:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int HPDataType;#include <stdio.h>
#include <assert.h>// 交换两个元素的值
void Swap(int* a, int* b)
{int temp;temp = *a;*a = *b;*b = temp;
}// 向上调整操作
void AdjustUp(int* a, int child)
{assert(a);int parent;while (child > 0){parent = (child - 1) / 2; // 计算父节点位置if (a[child] > a[parent]) // 如果子节点的值大于父节点的值{Swap(&a[child], &a[parent]); // 交换两个节点的值child = parent; // child 更新为 parent,继续向上比较}else{break;}}
}int main()
{int a[] = {10, 1, 3, 2, 4, 6, 8, 9, 7};int n = sizeof(a) / sizeof(int);int i;for (i = 0; i < n; i++){AdjustUp(a, i); // 对每个节点进行向上调整操作}for (i = 0; i < n; i++){printf("%d ", a[i]); // 输出调整后的数组}return 0;
}三、堆排序
堆排序是一种基于二叉堆(heap)数据结构的排序算法。它的思想可以概括为以下几个步骤:
-
构建堆:将待排序的数组视为一个完全二叉树,并将其转化为一个堆。这可通过从最后一个非叶子节点开始,逐个向上调整每个节点来完成。调整操作会使得当前节点和其子树满足堆的性质,即父节点的值大于等于(或小于等于)其子节点的值。这样就构建了一个最大堆(或最小堆)。
-
排序:经过构建堆操作后,堆顶元素是最大(或最小)的元素。我们可以将堆顶元素与堆中最后一个元素交换位置,然后将堆的大小减小 1。这样,最大(或最小)的元素会被放置到正确的位置(即最后一个位置)。接着,我们对堆顶元素进行向下调整,使得堆再次满足堆的性质。重复以上步骤,直到堆中只剩下一个元素。
-
返回有序序列:当堆中只剩下一个元素时,所有的元素都已经交换并放置到了正确的位置。此时,我们就得到了一个有序的序列。
堆排序的时间复杂度为 O(nlogn),其中 n 是数组的大小。它是一种原址排序算法,因为它只需要用到原始数组,不需要使用额外的空间。同时,堆排序也是一种稳定的排序算法。

代码及注释:
void AdjustDown(int* a, int parent, int n)
{// 计算左子节点的索引int child = parent * 2 + 1;// 当左子节点在数组范围内时进行循环while (child < n){// 如果右子节点存在且比左子节点大,则选择右子节点作为与父节点进行比较的子节点if (child + 1 < n && a[child] < a[child + 1]) {child++;}// 如果父节点小于子节点,则交换它们的值if (a[parent] < a[child]) {swap(&a[parent], &a[child]);// 更新父节点和子节点的索引parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{// 从最后一个非叶子节点开始,依次调用 AdjustDown 函数,构建最大堆int i = 0;int end = n / 2 - 1;for (i = end; i >= 0; i--){AdjustDown(a, i, n);}// 交换堆顶元素与最后一个元素,并向下调整堆for (i = 0; i < n; i++){swap(&a[0], &a[n - i - 1]);AdjustDown(a, 0, n - i - 1);}
}