🌮开发平台：jupyter lab

🍖运行环境：python3、TensorFlow2.x

----------------------------------------------- 2022.9.16 测验成功 ----------------------------------------------------------------
1. 时间序列预测：用电量预测 01 数据分析与建模
2. 时间序列预测：用电量预测 02 KNN（K邻近算法）
3. 时间序列预测：用电量预测 03 Linear（多元线性回归算法 & 数据未标准化）
4.时间序列预测：用电量预测 04 Std_Linear（多元线性回归算法 & 数据标准化）
5. 时间序列预测：用电量预测 05 BP神经网络
6.时间序列预测：用电量预测 06 长短期记忆网络LSTM
7. 时间序列预测：用电量预测 07 灰色预测算法

• 数据来源：Individual household electric power consumption Data Set（点击跳转数据集下载页面）

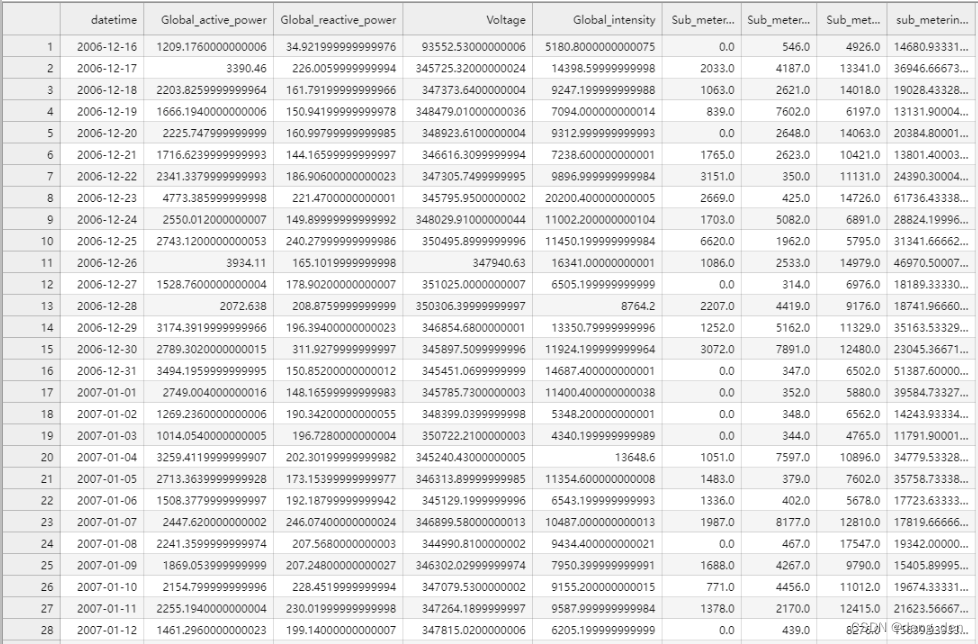
说明：根据上述列表中 1.时间序列预测：用电量预测 01 数据分析与建模 进行数据整理，得到household_power_consumption_days.csv文件，部分数据展示如下：

1.导包

## 灰色预测法（1，n）
## 训练数据和测试数据占比分别为0.7和0.3
from decimal import *
import matplotlib.pyplot as plt
import numpy as np
import pandas as pdimport warnings
warnings.filterwarnings('ignore')

2. 创建函数方法

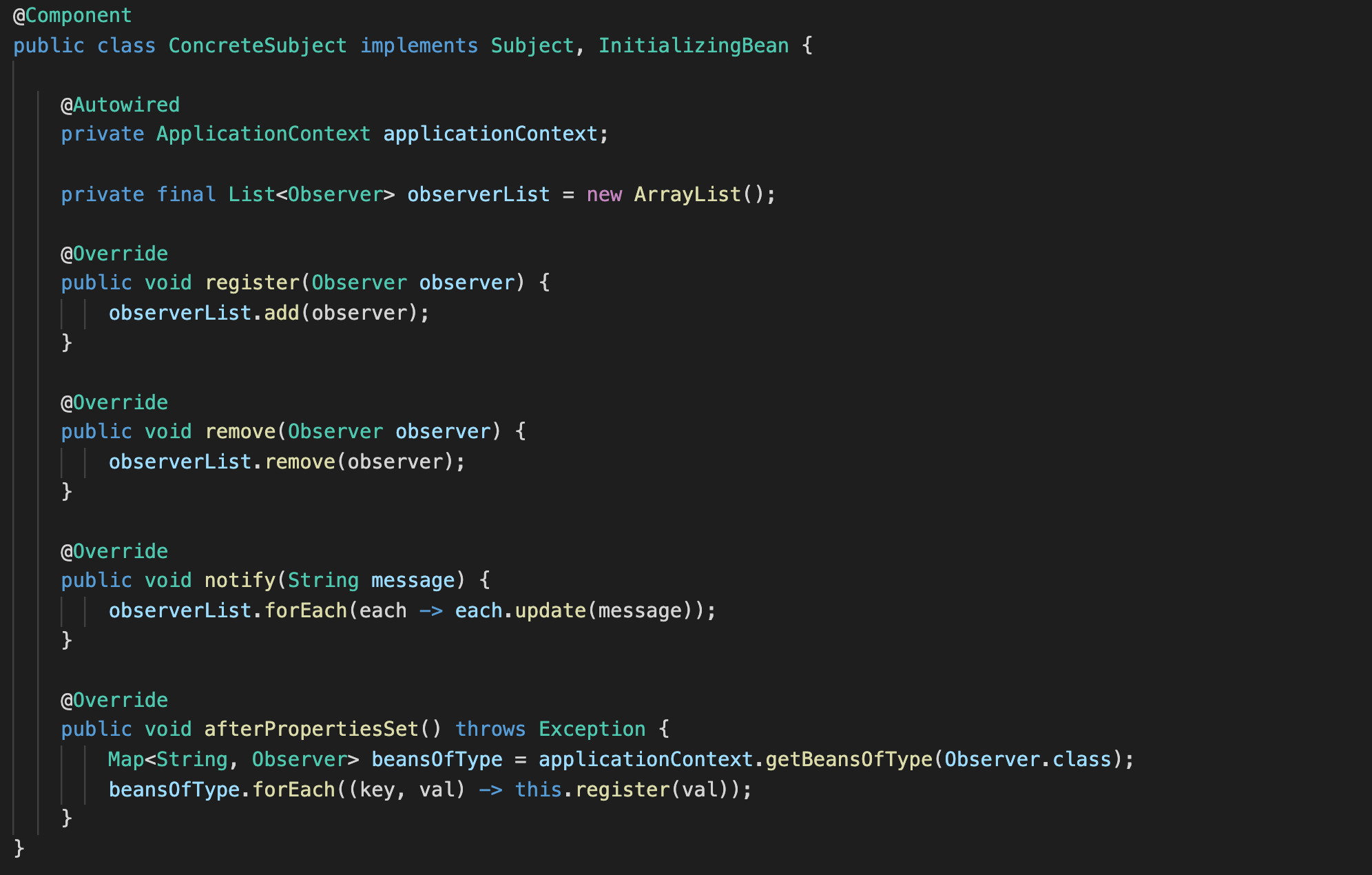
class GM11():def __init__(self):self.f = Nonedef isUsable(self, X0):'''判断是否通过光滑检验'''X1 = X0.cumsum()rho = [X0[i] / X1[i - 1] for i in range(1, len(X0))]rho_ratio = [rho[i + 1] / rho[i] for i in range(len(rho) - 1)]
#         print(rho, rho_ratio)flag = Truefor i in range(2, len(rho) - 1):if rho[i] > 0.5 or rho[i + 1] / rho[i] >= 1:flag = Falseprint("rho[-1]:"+str(rho[-1]))if rho[-1] > 0.5:flag = Falseif flag:print("数据通过光滑校验")else:print("该数据未通过光滑校验")'''判断是否通过级比检验'''lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]X_min = np.e ** (-2 / (len(X0) + 1))X_max = np.e ** (2 / (len(X0) + 1))for lambd in lambds:if lambd < X_min or lambd > X_max:print('该数据未通过级比检验')returnprint('该数据通过级比检验')def train(self, X0):X1 = X0.cumsum(axis=0)  # [x_2^1,x_3^1,...,x_n^1,x_1^1] # 其中x_i^1为x_i^01次累加后的列向量Z = (np.array([-0.5 * (X1[:, -1][k - 1] + X1[:, -1][k]) for k in range(1, len(X1[:, -1]))])).reshape(len(X1[:, -1]) - 1, 1)# 数据矩阵A、BA = (X0[:, -1][1:]).reshape(len(Z), 1)B = np.hstack((Z, X1[1:, :-1]))# 求参数u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)a = u[0][0]b = u[1:]print("灰参数a：", a, "，参数矩阵b：", b)self.f = lambda k, X1: (X0[0, -1] - (1 / a) * (X1[k, ::]).dot(b)) * np.exp(-a * k) + (1 / a) * (X1[k, ::]).dot(b)def predict(self, k, X0):''':param k: k为预测的第k个值:param X0: X0为【k*n】的矩阵,n为特征的个数，k为样本的个数:return:'''X1 = X0.cumsum(axis=0)X1_hat = [float(self.f(k, X1)) for k in range(k)]X0_hat = np.diff(X1_hat)X0_hat = np.hstack((X1_hat[0], X0_hat))return X0_hatdef evaluate(self, X0_hat, X0):'''根据后验差比及小误差概率判断预测结果:param X0_hat: 预测结果:return:'''S1 = np.std(X0, ddof=1)  # 原始数据样本标准差S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差C = S2 / S1  # 后验差比Pe = np.mean(X0 - X0_hat)temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率print('============= evaluate =============')print("原数据样本标准差：", S1)print("残差样本标准差：", S2)print("后验差：", C)print("小误差概率p：", p)

3.实验部分

3.1划分训练集和测试集

plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）
data = pd.read_csv('../1_Linear/household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# 原始数据X
X = data.values
## 按0.7和0.3的比例划分训练集
split_line = int(len(X)*0.7)
# 训练集
X_train = X[:split_line, :]
# 测试集
X_test = X[split_line:,:]## 数据量查看
len(X_train),len(X_test)  #out：(1009, 433)

3.2 评估模型，训练，并预测

# 特征数据集
model = GM11()
### 利用训练集判断模型可行性
model.isUsable(X_train[:, -1])  # 判断模型可行性
model.train(X_train)  # 训练## 利用训练集完成后的模型预测训练集的数据
X_train_pred = model.predict(len(X_train), X_train[:, :-1])  # 预测
score_train = model.evaluate(X_train_pred, X_train[:, -1])  # 评估## 利用训练集完成后的模型预测验证集的数据
Y_test_pred = model.predict(len(X_test), X_test[:, :-1])  # 预测
score_test = model.evaluate(Y_test_pred, X_test[:, -1])  # 评估

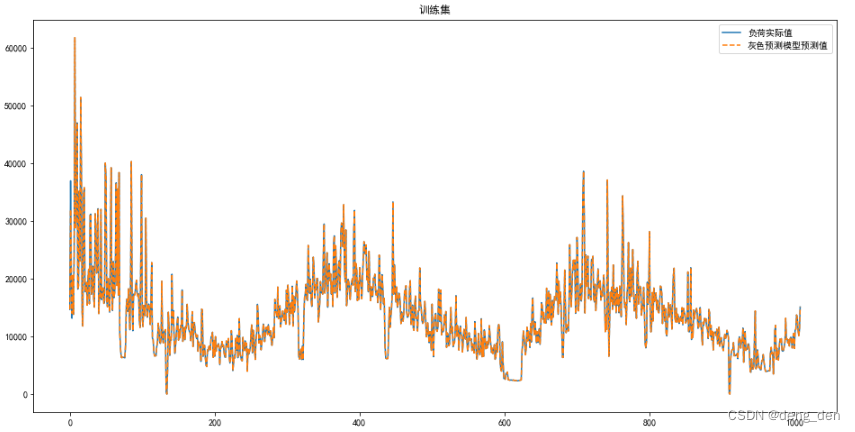
3.3 训练集和测试集 原始数据和预测值进行对比

#训练集可视化
plt.figure(figsize=(16,8))
plt.plot(np.arange(len(Y_train_pred)), X_train[:, -1], '-')
plt.plot(np.arange(len(Y_train_pred)), Y_train_pred, '--')
plt.legend(['负荷实际值', '灰色预测模型预测值'])
plt.title('训练集')
plt.show()

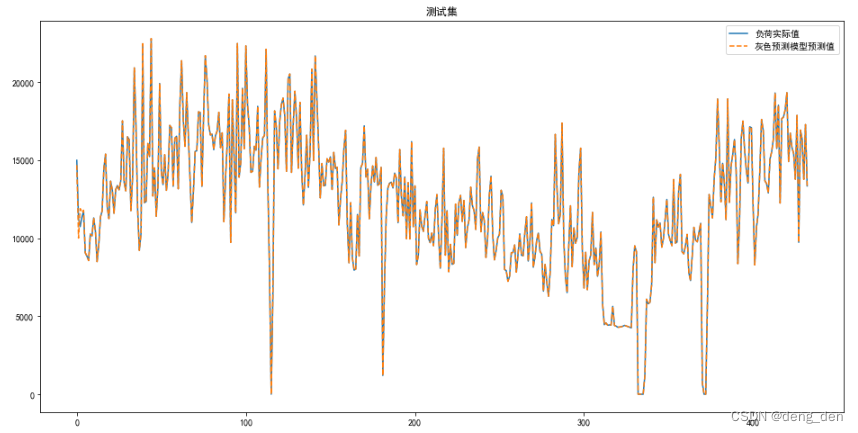
# 验证集可视化
plt.figure(figsize=(16,8))
plt.plot(np.arange(len(Y_test_pred)), X_test[:, -1], '-')
plt.plot(np.arange(len(Y_test_pred)), Y_test_pred, '--')
plt.legend(['负荷实际值', '灰色预测模型预测值'])
plt.title('测试集')
plt.show()

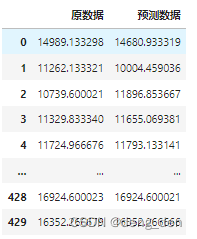
3.4 以表格形式对比测试集原始目标数据和预测目标数据

# 1.判断数据类型
type(X_test[:, -1]),type(Y_test_pred)  #out：(numpy.ndarray, numpy.ndarray)
# 2.预测数据对比
## 预测数据对比
compare = pd.DataFrame({"原数据":X_test[:, -1],"预测数据":Y_test_pred})
compare

3.5 随机编写数据进行测验

• 随机编写2个数据，真实目标列值为：16983.666650、11329.833340,这里改为了500、300,参照下表头两行数据修改
  

### 随机编写2个数据，真实目标列值为：16983.666650、11329.833340,参照上表头两行数据
data_random = [[1941.940,154.028,347746.67,8210.4,3712.0,4357.0,7300.0,500],[1636.610,235.964,346675.11,6947.6,2085.0,970.0,12884.0,300]]
X_random = np.array(data_random)## 对数据进行预测
Y_random_pred = model.predict(len(X_random), X_random[:, :-1])  # 预测
print(Y_random_pred)
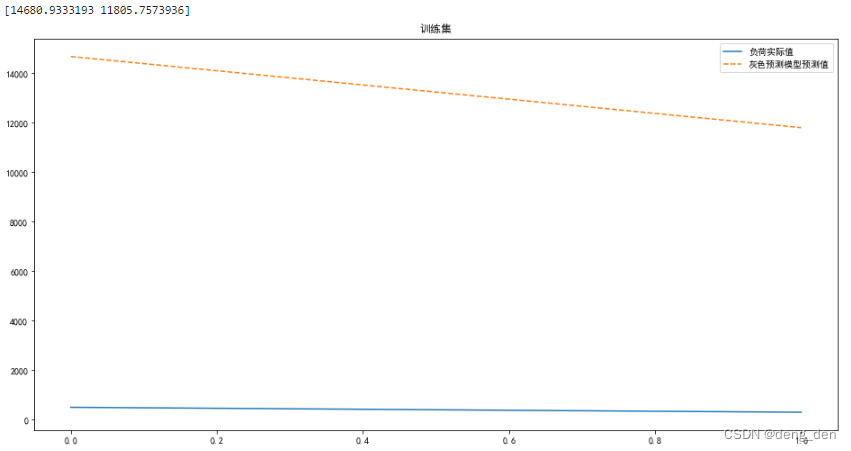
#训练集可视化
plt.figure(figsize=(16,8))
plt.plot(np.arange(len(Y_random_pred)), X_random[:, -1], '-')
plt.plot(np.arange(len(Y_random_pred)), Y_random_pred, '--')
plt.legend(['负荷实际值', '灰色预测模型预测值'])
plt.title('训练集')
plt.show()
# out：[14680.9333193 11805.7573936]