目录

1 乘法

1.1 标量乘法(中小学乘法)

1.1.1 乘法的定义

1.1.2 乘法符合的规律

1.2 向量乘法

1.2.1 向量：有方向和大小的对象

1.2.2 向量的标量乘法

1.2.3 常见的向量乘法及结果

1.2.4 向量的其他乘法及结果

1.2.5 向量的模长（长度）

模长的计算公式

1.2.6 距离

2 向量的各种乘法

2.1 向量的标量乘法（即：向量乘1个常数）

2.2 通用的向量/矩阵乘法  (Matrix Multiply)

2.3 向量的内积(数量积) inner product

2.3.1 内积的定义（适合N维空间中）

2.3.2 内积的计算公式：

2.3.3 内积乘法符合的规律

2.3.4 内积的几何意义

2.4 向量的点积 (标准内积/欧几里得内积) Dot product

（二维空间 ，勉强三维空间）

2.4.1 内积和点积的区别: 点积是欧几里得内积，是内积的特例

2.4.2 内积和外积的几何意义的区别

2.4.3 点积除了二维空间，还可以三维空间应用吗？

2.4.4 点乘和点积的定义

2.4.5 点积符合的规律

2.4.6 点积的几何意义

内积的公式可以理解为往另外一个向量的投影

EXCEL里cos(θ) 的计算

cos曲线          

最大值 ，最小值和90度正交        

2.4.7 向量点积的分界线

2.4.8 点积的应用

2.5 向量的外积  outer product

2.5.1 外积的定义

2.5.2 外积的公式

2.5.3 外积的几何意义

2.6 向量的叉积cross product （3维空间，勉强2维空间）

2.6.1 向量的叉积的定义

2.6.2  向量的叉积的适用范围

2.6.3  向量的叉积的公式

2.6.4 叉积符合的规律

2.6.5 向量的叉积的几何意义

2.7 向量的混合积

2.7.1 混合积

2.8 直积/笛卡尔乘积

2.8.1 直积的定义Cartesian product

2.8.3 笛卡尔乘积的公式

2.9 克罗内克积, Kronecker product

2.9.1 克罗内克积的定义

2.9.2 计算公式

2.10 哈达玛积 Hadamard product

2.10.1 哈达玛积定义

2.10.2 计算公式

2.11 张量积 tensor product)

2.11.1 张量积的定义

2.12 总结（很多深度知识不懂，暂时这么总结吧 - -！）

3 用EXCEL和python计算向量的点积和叉积

（以后看看有没必要加VBA的）

3.1 EXCEL里矩阵计算的相关公式

3.2 EXCEL如何计算2个向量的点积，叉积

3.2.1 EXCEL计算2个向量的点积的方法

​编辑

3.2.2 用EXCEL计算两个向量叉积的方法

3.2.3 用EXCEL计算2个2维向量的点积和叉积

3.2.4 用EXCEL计算2维向量的点积和叉积

​编辑

3.3  用python的 numpy 计算两个向量的内积

3.3.1 numpy相关的点乘和叉乘公式

3.3.2 numpy分别计算2维向量的点积和叉积

3.3.3 numpy分别计算3维向量的点积和叉积

4 用EXCEL和python计算向量组的点积和叉积

4.1 EXCEL里计算向量组的点积

4.1.1 EXCEL向量组的点积公式

4.1.2 EXCEL里向量组的叉积公式

4.1.3 下面是2维矩阵和3维矩阵的点积，叉积的计算

4.2 python里向量组/矩阵的乘法

4.2.1 关于2个2*2矩阵的点积和叉积

4.2.2  关于2个3*3矩阵的点乘和叉乘

5 点积和叉积的数学计算总结

5.1 点积计算

5.1.1 如果是向量的点积

5.1.2 如果是矩阵的点积

5.2 叉积计算

5.2.1 向量的的叉积计算

5.2.2 矩阵的叉积计算

5.3 向量的点积，叉积

5.4 矩阵的点积，叉积

---

1 乘法

1.1 标量乘法(中小学乘法)

1.1.1 乘法的定义

• 乘法的定义

1. a*b= a个b之和
2. a*b= a 的 b 倍
3. 2*3=3+3=6
4.  

1.1.2 乘法符合的规律

• 交换律 ：a*b= b*a
• 分配律：c*(a+b) =c*a+c*b
• 结合律：c*(a*b)= (c*a)*b

1.2 向量乘法

1.2.1 向量：有方向和大小的对象

1. 向量只有方向和大小
2. 没有具体的位置

1.2.2 向量的标量乘法

• 如果一个标量和向量相乘
• 标量*向量
• λ*A = λ* 向量A的每个元素

1.2.3 常见的向量乘法及结果

• 向量的内积 inner product
• 向量的点积 dot product
• 向量的外积 outer product
• 向量的叉积 cross product
• 点积是降维
• 叉积是升维

1.2.4 向量的其他乘法及结果

• 克罗内克积, Kronecker product
• 等等

1.2.5 向量的模长（长度）

• 在二维平面上，一个向量的模长就是线段的长度。但是维度高了，就要用模长。
• 向量的模长，也被称作向量的大小或者绝对值
• 是用来描述向量的长度的数学概念。
• 在高维空间中，虽然我们无法直观地看到向量，但是我们仍然可以通过计算来得到向量的模长。

模长的计算公式

• 对于一个n维向量v = (v1, v2, …, vn)
• 其模长||v||可以通过以下公式计算：
• ||v|| = sqrt(v1^2 + v2^2 + ... + vn^2)
• 所以，向量的模长实际上就是其各分量平方和的平方根。

1.2.6 距离

距离类型

• 欧氏距离
• 曼哈顿距离
• 等等

这里的距离，一般都是欧氏距离

• 欧氏距离
• distance(a,b)=sqrt((a-b)*(a-b))
• 欧氏距离=坐标轴里每个分量相减平方和再开方
• distance(a,b)sqrt((Va1-Vb1)^2 + (Va2-Vb2)^2 + ... + (Van-Vbn)^2)

2 向量的各种乘法

2.1 向量的标量乘法（即：向量乘1个常数）

• 向量的标量乘法
• λ是标量，数字，不是向量

公式

• λ*A = λ* 向量A的每个元素
• λ*A= λ*[a11,a12 ... a1m] =[λ*a11,λ*a12 ... λ*a1m]

其中

• 矩阵的标量乘法  λ*A=λ*每个元素，*A*B=A*λ*B
• 行列式的标量乘法，λ*|A|=λ*某1行/列

2.2 通用的向量/矩阵乘法  (Matrix Multiply)

• Standard matrix multiplication
• 最一般的矩阵间乘法
• 矩阵乘法 (Matrix Multiply)
• 用于矩阵相乘，A，B均为矩阵，A的维度为m*p，B的维度为p*n，则A*B的结果为m*n的矩阵。
• 矩阵乘法是通用的，所有向量，矩阵理论上都可以按此计算，但是有一个前提要求:
• 必须满足：左边的矩阵A(n*p) 列数p= 右边矩阵B(p*m)的行数p 

公式

• 矩阵乘法的公式 C=A*B
• 是C的每个元素，cij=Σ a的第1行*b的第1列
• 公式

2.3 向量的内积(数量积) inner product

2.3.1 内积的定义（适合N维空间中）

• inner product
• 是接受在实数R上的两个向量并返回一个实数值标量的二元运算
• 名称：向量的数量积，向量的内积，矩阵的内积
• 相关概念
• Inner product space

2.3.2 内积的计算公式：

• 两个向量的分量相乘然后相加求和，结果是1个标量
• 内积的要求：
• 两个向量完全相同A(n)∙ B(n)
• 两个向量组/矩阵完全相同A(m,n)∙ B(m,n)

公式

• N维空间中 A(n)∙ B(n)=a1b1+a2b2+.....an*bn=Σaibi
• 

2.3.3 内积乘法符合的规律

• 交换律 ：a∙b= b∙a
• 分配律：k*(a+b) =k*a+k∙b
• 结合律：c∙(a∙b)= (c∙a)∙b
• 对称性：a∙b= b∙a
• 正定性：对于任何非零向量a， a∙a>0

2.3.4 内积的几何意义

• 内积和点积，都是用来衡量两个向量方向上的相似性的
• 内积因为维度不只是二维三位，角度不好表示，所以只判断内积的正负
• 内积=0，两个向量垂直正交
• 内积大于0，两个向量的方向相似
• 内积小于0，两个向量的方向相反

2.4 向量的点积 (标准内积/欧几里得内积) Dot product

（二维空间 ，勉强三维空间）

2.4.1 内积和点积的区别: 点积是欧几里得内积，是内积的特例

• 内积：N维空间都生效
• 点积：多用于欧氏空间，主要用于二维的(所以被称为 欧几里得内积)
• 所以，点积是内积的一种特殊情况？
• 其实我并不清楚，内积除了点积外还有哪些其他形式？
• 我现在只能理解为，点积是内积在二维空间的表现形式

2.4.2 内积和外积的几何意义的区别

• a·b=|a||b|·cosθ
• 几何意义，向量a在向量b方向上的投影与向量b的模的乘积。
• 内积是把a向量投影到b向量上面，让两者同向或者反向，让a向量箭头指向b向量相同，让两个向量共线，可以认为在向量里面，所以叫内积。
• 因此，内积两个向量谁投影谁都可以，因为最后是一个标量，没有方向性。
• 而外积是把a向量投影到b向量的法线方向，投影到向量的外部（最外部的方向就是法线/垂直/正交的方向），二者几何意义生成的新向量，就是这2个向量组成的法向量，所以叫外积。

• 外积就不一样了，一定是A投影B，因为要用右手确定结果向量的方向，有前后顺序之分。否则就是反方向，负交换律，A*B = - B*A

2.4.3 点积除了二维空间，还可以三维空间应用吗？

• 点积在二维空间，a*b=|a||b|*cosθ
• 点积在三维空间，a*b=|a||b|*cosθ
• 我觉得三维空间也可以
• a,b 只是表示乘3维空间的坐标形式即可,比如a(a1*i,a2*j,a3*j) ,b(b1*i,b2*j,b3*j) 
• 因为3维空间里也有2维空间，也可以算出cosθ

2.4.4 点乘和点积的定义

点乘：(Pointwise Multiply)

• Pointwise Multiply
• 点乘的结果就是点积

点积

• 点积, 也标准内积，欧几里得内积
• dot product 

公式

• 用于矩阵相乘，A，B为维度大小完全相同的矩阵
• 即A的行数=B的行数，A的列数=B的列数，
• 实际计算的时候，
• 点积=行向量*列向量
• 在运算时，AB矩阵的对应位置的元素相乘。若AB均为mn的矩阵，则其点乘的结果仍为一个mn的矩阵。
• 两个向量的分量相乘然后相加求和

1. 公式1：a*b=Σ(a1b1+a2b2+.....anbn)
2. 公式2：点积=行向量*列向量
3. 公式3：二维空间中，a*b=|a||b|*cosθ

2.4.5 点积符合的规律

• 交换律：a∙b= b∙a
• 分配律：k*(a+b) =k*a+k∙b
• 结合律：c∙(a∙b)= (c∙a)∙b
• 任何向量*0向量=0向量
• 方向性

1. 0-90度 ,点积>0 ,两个向量方向相同
2. 90 点积=0,向量垂直正交
3. 90-180 ,点积<0 ,两个向量方向相反
4. 180-270 ,点积<0
5. 270-360 ,点积>0

2.4.6 点积的几何意义

• 夹角 ：两个向量的夹角，判断向量之间的方向的相似性
• 投影：1个向量在另外一个向量方向上的投影，再计算
• 正交性：点积=0，两个向量垂直正交

关于两个向量的夹角

• a*b=|a||b|*cosθ
• 两个单位向量的点积得到两个向量的夹角的cos值，通过它可以知道两个向量的相似性。
•  内积的公式  A*B=|A|*|B|*cos(θ)     
•  向量的内积 W*X=WT*X=|W|*|X|*cos(θ)        

内积的公式可以理解为往另外一个向量的投影

• A*B=|A|*|B|*cos(θ)            
• A*B=|A|*(|B|*cos(θ))            
• A*B=|B|*(|A|*cos(θ))         
• 内积=一个向量投影到另外一个向量上的分量*另外一个向量            
• 因此2个向量垂直90°时,向量的分量投影=0，因此内积=0          

EXCEL里cos(θ) 的计算

• EXCEL里cos(θ) ，其中θ 必须是弧度
• 弧度=角度*PI()/180
• 弧度=RADIANS(角度)

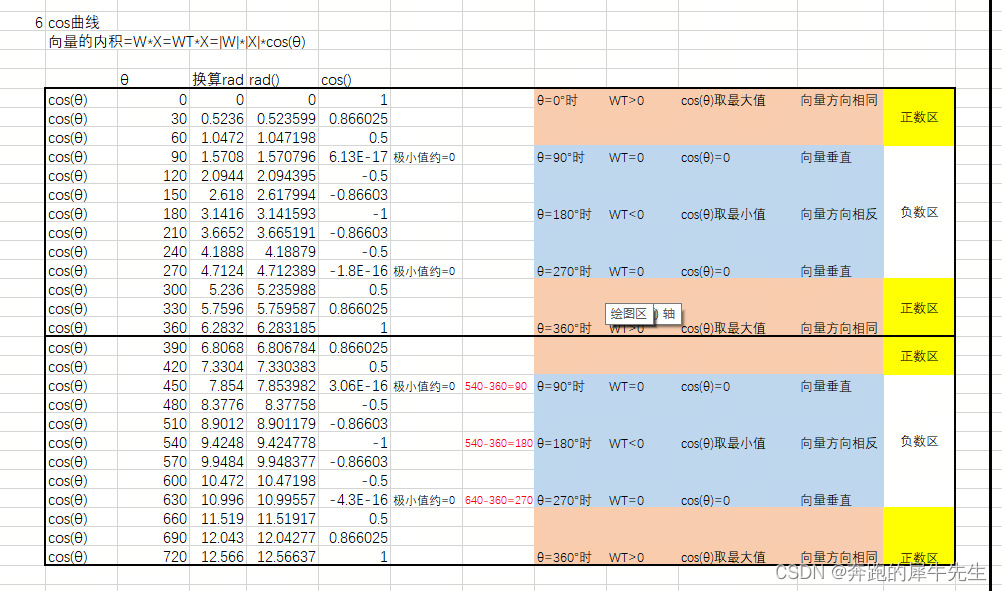
cos曲线          

• cos(θ)  曲线的特点

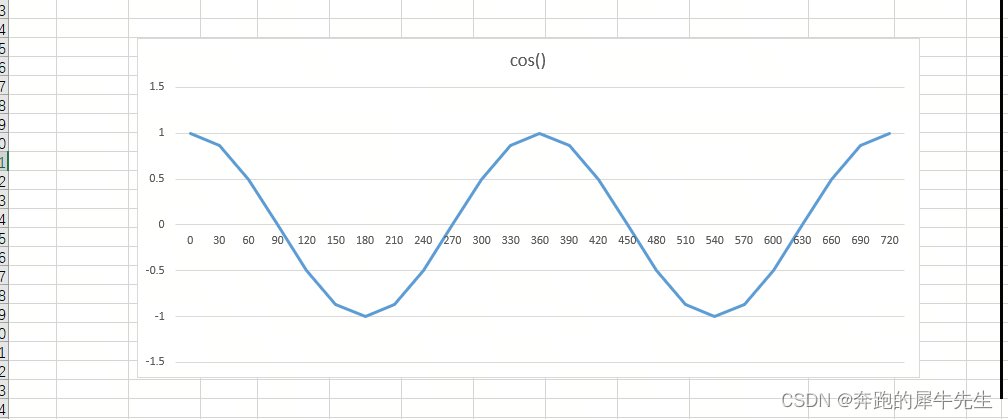
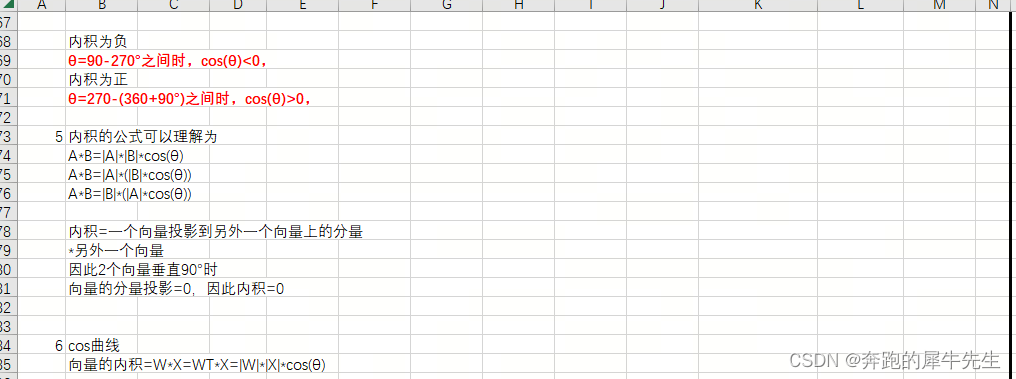
最大值 ，最小值和90度正交        

•     A*B=|A|*|B|*cos(θ)            
•     当其他条件|A| |B| 的模长不变时，            
•     θ=0°，cos(θ)=1，向量平行/共线，内积最大                               
•     θ=180°，cos(θ)=-1 ，向量方向相反，内积最小，为负数     
•     θ=90°，cos(θ)=0    两个向量内积为0 ，必然两个向量垂直/正交 

2.4.7 向量点积的分界线

• 向量的内积=0，形成的一条直线，可以作为分界线
• 向量的内积大于0，就是直线的一边
• 向量的内积小于0，直线的另外一边
• 可以用来机器学习里的有监督学习的数据分类时使用此方法

2.4.8 点积的应用

• 利用点积可判断一个多边形是面向摄像机还是背向摄像机。
• 向量的点积与它们夹角的余弦成正比，因此在聚光灯的效果计算中，可以根据点积来得到光照效果，如果点积越大，说明夹角越小，则物体离光照的轴线越近，光照越强。

2.5 向量的外积  outer product

2.5.1 外积的定义

• outer product
• 矢积/外积/向量积
• 数学中又称外积、向量积，物理中称矢积、叉乘
• 是一种在向量空间中向量的二元运算。
• 与点积不同，它的运算结果是一个向量而不是一个标量。

向量外积，Outer product

•  符号为 × 
•  外积结果是一个矩阵，外积的计算过程等价于矩阵的Standard matrix multiplication，就是常规的矩阵计算乘法。

2.5.2 外积的公式

• 公式表示：c=a× b，
• 计算结果是向量：a× b的结果是一个垂直于a,b向量屏幕的法线向量。
• 外积的大小：|c|=|a× b|=|a|*|b|*sin(a,b)
• 外积的方向：

1. 右手定则：若坐标系是满足右手定则的
2. 设z=x×y,|z|=|x||y|*sin(x,y)，则x,y,z构成右手系，伸开右手手掌，四个手指从x轴正方向方向转到y轴正方面，则大拇指方向即为z正轴方向。

2.5.3 外积的几何意义

• c=a× b
• |c|=|a× b|=|a|*|b|*sin(a,b)
• c的方向遵守右手定则，几何意义，c是垂直a、b所在平面，且以|b|·sinθ为高、|a|为底的平行四边形的面积。

2.6 向量的叉积cross product （3维空间，勉强2维空间）

2.6.1 向量的叉积的定义

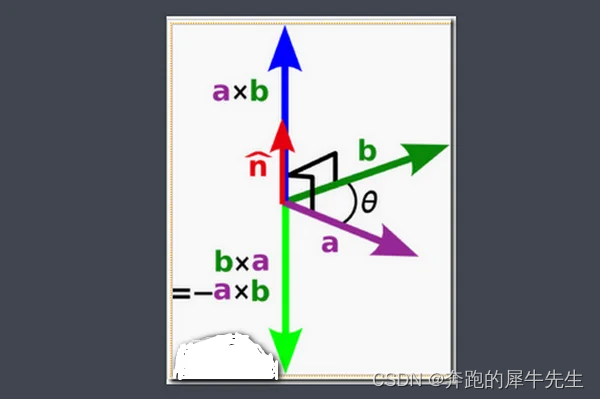
表示方法：两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。

• cross product
• 叉积 、向量积、vector product等。
• 向量的叉积是向量外积特例？
• 符号为 x

2.6.2  向量的叉积的适用范围

• 叉积运算只定义在三维空间，结果仍然是一个向量
• 理论上看起来，cross product 叉积的结果应该是一个3维空间内的法向量，
• 但是当2个向量都是2维向量时，算出的叉积也是一个法向量，但不应该是2维的，所以叉积只能理解为这2个向量组成的面积。

2.6.3  向量的叉积的公式

• 叉积运算只定义在三维空间，结果仍然是一个向量
• 其方向遵循右手定则。
• 外积的坐标表示：
• (x1,y1,z1)×(x2,y2,z2)=(y1z2-y2z1,z1x2-z2x1,x1y2-x2y1)

2.6.4 叉积符合的规律

• 反交换律：AxB=-BxA
• 结合律：AxB

2.6.5 向量的叉积的几何意义

• 向量的叉积 c=a× b，那么叉积的长度是|c|=|a× b|=|a|*|b|*sin(a,b)，向量的叉积a×b的长度|a×b|，可以解释成这两个叉乘向量a，b共起点时，所构成平行四边形的面积。
• 并且两个向量的叉积与这两个向量和垂直。

2.7 向量的混合积

2.7.1 混合积

• 向量的叉积 c=a× b，那么叉积的长度是|c|=|a× b|=|a|*|b|*sin(a,b)，向量的叉积a×b的长度|a×b|，可以解释成这两个叉乘向量a，b共起点时，所构成平行四边形的面积。
• 而向量的混合积[abc] =(a×b)·c ,可以得到以a，b，c为棱的平行六面体的体积。

2.8 直积/笛卡尔乘积

2.8.1 直积的定义Cartesian product

• 在数学中，两个集合X和Y的笛卡尔积（Cartesian product），又称笛卡尔乘积，
• 表示为X × Y，第一个对象是X的成员，第二个对象是Y的所有可能成员，而可能组成的有序对的其中一个成员。
• 设A,B为集合，用A中元素为第一元素，B中元素为第二元素构成有序对，所有这样的有序对组成的集合叫做A与B的笛卡尔积，记作AxB。

2.8.2 用实例在理解笛卡尔乘积

• 如果A表示某学校学生的集合，B表示该学校所有课程的集合，则A与B的笛卡尔积表示所有可能的选课情况。A表示所有声母的集合，B表示所有韵母的集合，那么A和B的笛卡尔积就为所有可能的汉字全拼。

2.8.3 笛卡尔乘积的公式

2.9 克罗内克积, Kronecker product

2.9.1 克罗内克积的定义

• Kronecker product[6]，克罗内克积
• 克罗内克积是一种特殊的张量积？
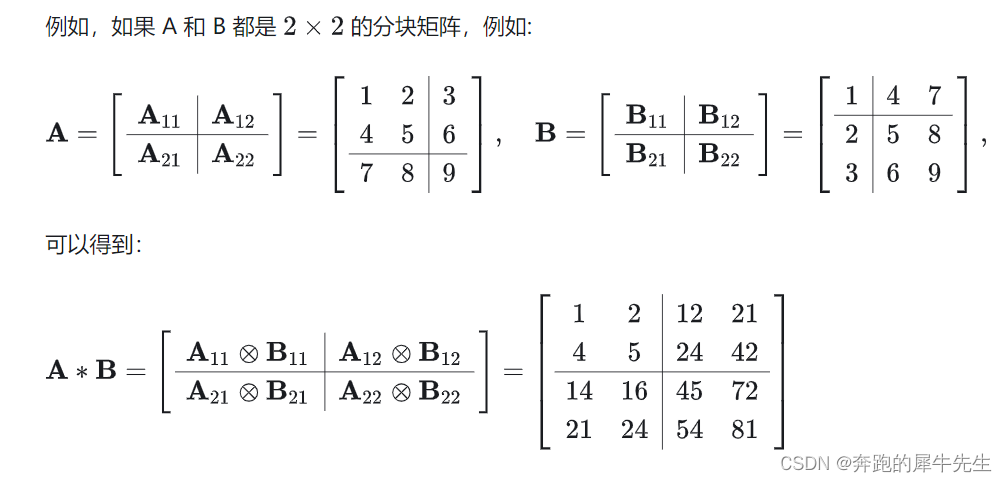
• 是的向量外积(out product)的推广，形成的是分块矩阵(block matrix)，对矩阵维度没有要求。又称：matrix direct product等。
• 比最常规的矩阵乘法还要更普适，因为可以对2个相乘的矩阵维度没有要求。用分开矩阵的方法计算
• 可以认为：外积，叉积都是属于 克罗内克积了。

2.9.2 计算公式

2.10 哈达玛积 Hadamard product

2.10.1 哈达玛积定义

• 哈达玛积
• 又称：逐元素积、element-wise product、entrywise product、Schur product等。
• 符号为 
•  矩阵对应元素相乘，要求矩阵维度相同（要求2个矩阵完全相同）。
• 从计算上看，内积和点积都属于哈达玛积？
• 而点积就是哈达玛积在二维空间的一种特殊情况？

2.10.2 计算公式

•  矩阵对应元素相乘，要求矩阵维度相同。

2.11 张量积 tensor product)

2.11.1 张量积的定义

• ⊗ \otimes⊗ 张量积
• “张量积” 可以扩展到一般范畴。
• 凡是在范畴中多个对象得到一个对象，并满足一定结合规则和交换规则的操作都可以视为 “张量积”，比如集合的笛卡儿积，无交并，拓扑空间的乘积，等等，都可以被称为张量积。
• 可以应用于不同的上下文中如向量、矩阵、张量、向量空间、代数、拓扑向量空间和模。
• 在各种情况下这个符号的意义是同样的：
• 最一般的双线性运算。在某些上下文中也叫做外积。例如：

2.12 总结（很多深度知识不懂，暂时这么总结吧 - -！）

• 点积 ⊆ 内积 ⊆ 哈达玛积
• 叉积 ⊆ 外积 ⊆克罗内克积 ⊆ 张量积
• 笛卡尔乘积

3 用EXCEL和python计算向量的点积和叉积

（以后看看有没必要加VBA的）

• 向量，这里是至一维向量
• 向量=行向量=列向量
• 向量组=矩阵

3.1 EXCEL里矩阵计算的相关公式

• 向量组相乘 ：mmult() ，计算矩阵的相乘
• 向量组转置 ：transpose() ，矩阵转置，比如行向量转为列向量
• 向量组取逆 ：minverse() ，计算矩阵的逆矩阵，满秩的矩阵才有逆矩阵，并不是都会有逆矩阵
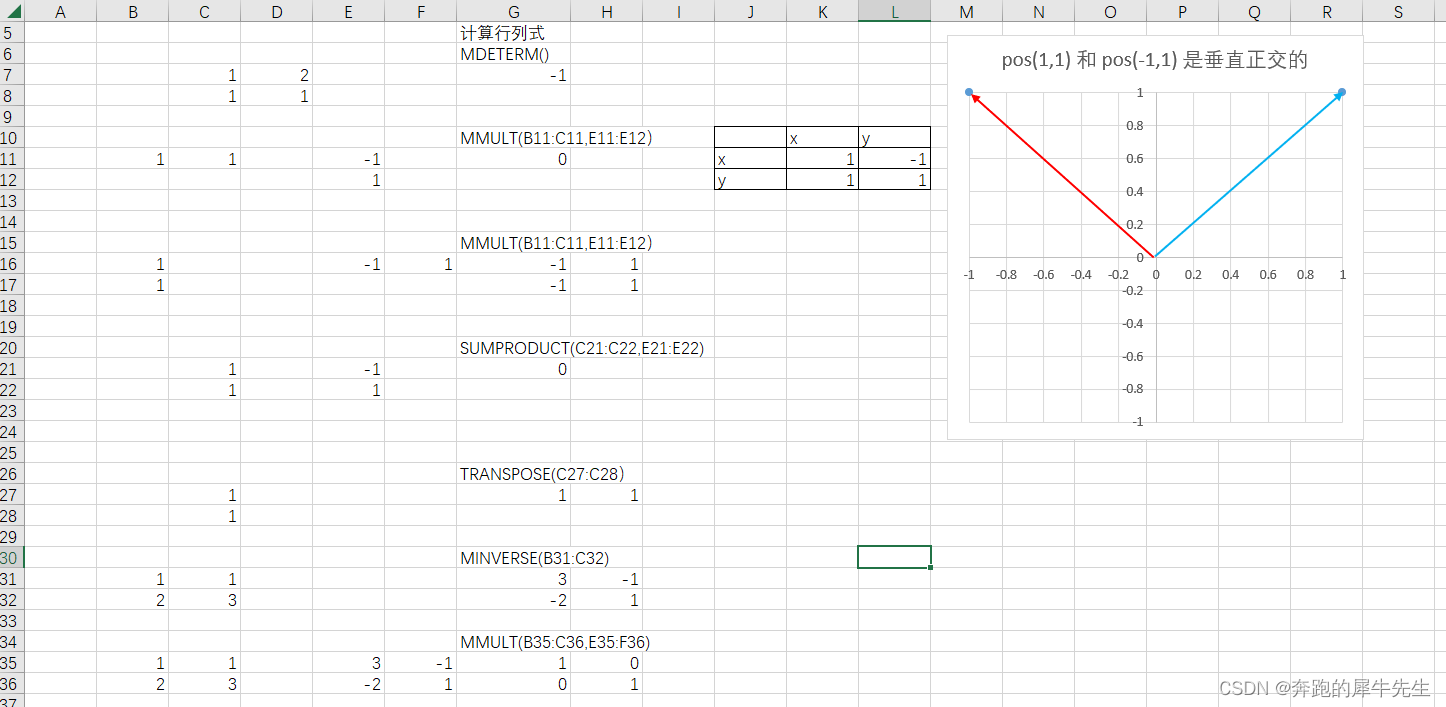
• 行列数公式： MDETERM()，计算矩阵的行列式的值。

测试

• 注意向量的计算，再EXCEL都要用数组公式
• 用mmult() 计算矩阵乘积，行向量*列向量=点积
• 用mmult() 计算矩阵乘积，列向量*行向量=新的矩阵~
• transpose() 转置，可以转置行向量--列向量
• minverse()求逆矩阵，
• 矩阵*逆矩阵=单位矩阵

3.2 EXCEL如何计算2个向量的点积，叉积

3.2.1 EXCEL计算2个向量的点积的方法

• 两个向量的点积=行向量*列向量 = 常数/标量
• sumproduct() 函数刚好是，对应元素相乘后求和，契合点积公式
• mmult() 函数，mmult(行向量，列向量) 也可以计算点积

• EXCEL计算点积的注意点

1. 向量的点积: 可以用mmult() 或 sumproduct()
2. 矩阵的点积: 只能用sumproduct()

首先要注意，两个向量要完全相同才可以计算点积

方法1：两个向量相乘的公式，向量的内积=mmult(行向量*列向量)

• 如果行列向量设置不对，计算时记得用 transpose()
• 所有矩阵的相乘都可以用muult() ，但是点积的计算要注意矩阵的维度。
• 比如：向量 A(1*n) B(n*1)= 内积C(1*1)
• 但是：向量 A(n*1) B(1*n)= C(n*n) 这个不是内积

方法2：用sumproduct() 可以直接计算点积，点积定义符合 对应元素相乘再求和
 

3.2.2 用EXCEL计算两个向量叉积的方法

• 两个向量的叉积计算公式这样
• 类行列数的计算方法

1. 但是第1行要补充为 x,y,z 或者 i,j,k 这3个坐标轴的基向量
2. 第2行是第2个向量
3. 第3行是第3个向量
4. 计算公式

1. A=[x1,y1,z1] B=[x2,y2,z2]
2. C=A*B=[y1z2-z1y2,z1x2-x1z2,x1y2-y1x2]

3.2.3 用EXCEL计算2个2维向量的点积和叉积

• 测试情况和上面的方法相同

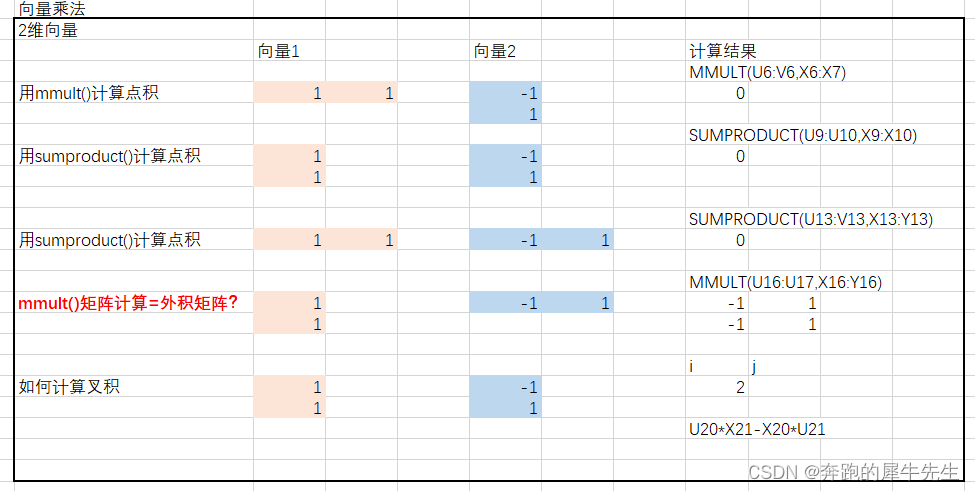
3.2.4 用EXCEL计算2维向量的点积和叉积

• 测试结果和上面方法的结果相同

3.3  用python的 numpy 计算两个向量的内积

3.3.1 numpy相关的点乘和叉乘公式

• 点乘： np.dot()
• 叉乘： np.cross()

3.3.2 numpy分别计算2维向量的点积和叉积

• 2 维向量，不是矩阵，dimension(1*2)
• 计算2维 向量的点积，np.dot()
• 计算2维 向量的叉积，np.cross()
• 而如果用 A*B的*号，以及np.multiply，计算出来的结果是都是对应元素相乘。也就是像哈达玛积。

• 理论上看起来，cross product 叉积的结果应该是一个法向量，但算出来是个常量
• 因为再二维空间下，叉积只能是无方向的两个向量叉积对应的面积。
• 但是当2个向量都是2维向量时，算出的叉积也是一个法向量，但不应该是2维的。所以叉积只能理解为这2个向量组成的面积。

import numpy as np# 两个2维向量（非向量组）的乘法
A=np.array([1,1])
B=np.array([-1,1])
print("两个2维向量（非向量组）的乘法:")#np.dot 的结果是点积？
C=np.dot(A,B)
print(f"C=np.dot(A,B)={C}")#np.cross 的结果是叉积？
C=np.cross(A,B)
print(f"C=np.cross(A,B)={C}")#A*B 的结果是对应元素相乘
C=A*B
print(f"C=A*B={C}")#np.multiply 的结果是对应元素相乘
C=np.multiply(A,B)
print(f"C=np.multiply(A,B)={C}")

两个2维向量（非向量组）的乘法:
C=np.dot(A,B)=0
C=np.cross(A,B)=2
C=A*B=[-1  1]
C=np.multiply(A,B)=[-1  1]

3.3.3 numpy分别计算3维向量的点积和叉积

• 和2维向量计算基本相同
• np.dot()   ,计算3维向量的点积，
• np.cross ,计算3维向量的叉积，
• A*B   ，计算出来的结果是都是对应元素相乘
• npmultiply(A,B) ，计算出来的结果是都是对应元素相乘，都像哈达玛积

import numpy as npA=np.array([1,0,0])
B=np.array([0,1,0])
print("两个3维向量（非向量组）的乘法:")C=np.dot(A,B)
print(f"C=np.dot(A,B)={C}")C=np.cross(A,B)
print(f"np.cross={C}")C=A*B
print(f"A*B={C}")C=np.multiply(A,B)
print(f"np.mutliply(A,B)={C}")

两个3维向量（非向量组）的乘法:
C=np.dot(A,B)=0
np.cross=[0 0 1]
A*B=[0 0 0]
np.mutliply(A,B)=[0 0 0]

4 用EXCEL和python计算向量组的点积和叉积

4.1 EXCEL里计算向量组的点积

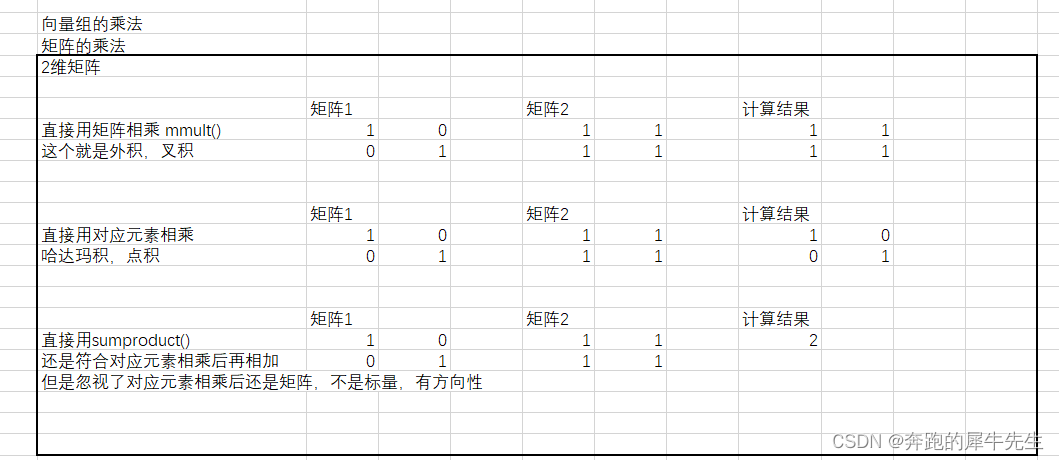
4.1.1 EXCEL向量组的点积公式

• mmult(矩阵A，矩阵B) 计算的结果就是点积
• sumproduct计算的不是内积了！（只有2个向量的内积才能刚好碰巧用sumproduct()计算）
• 矩阵的内积，就是对应元素相乘的哈达玛积
• 计算方法，就是EXCEL里直接2个同型矩阵，对应元素相乘即可。

4.1.2 EXCEL里向量组的叉积公式

• 直接用 mmult() 矩阵相乘即可

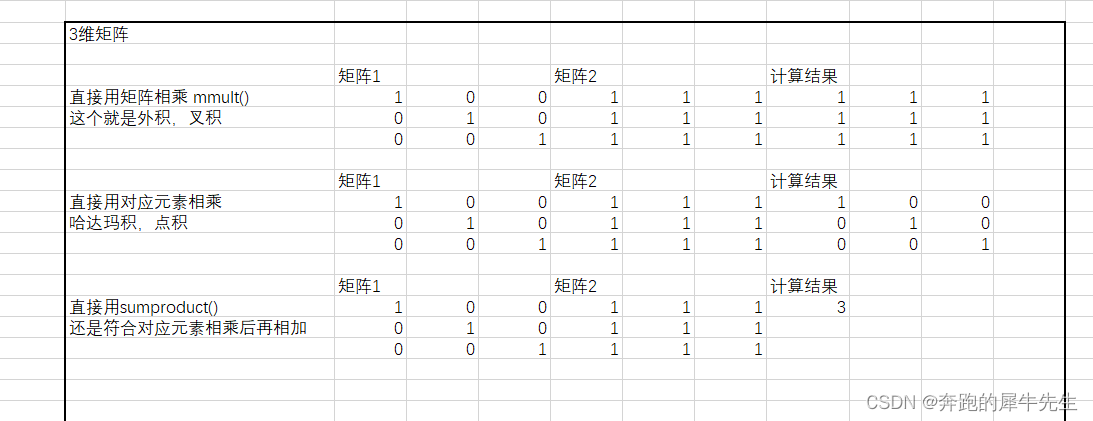
4.1.3 下面是2维矩阵和3维矩阵的点积，叉积的计算

4.2 python里向量组/矩阵的乘法

4.2.1 关于2个2*2矩阵的点积和叉积

• 和向量的计算完全不同！！
• 矩阵的点积

1. 这两种方法计算出来的都是点积，也就是哈达玛积？
2. A*B，计算出来的结果是都是对应元素相乘
3. npmultiply(A,B) ，计算出来的结果是都是对应元素相乘

• 矩阵的叉积

1. np.dot()  ,计算矩阵的叉积 (向量用np.dot() 算出来的是点积)
2. np.matmul() , ,计算矩阵的叉积
3. A@B  ,计算矩阵的叉积

• np.cross  ，计算出来的结果是什么？？？
• 暂时不知道

• 对于向量，使用dot函数完成向量的点乘
• 对于矩阵，使用multiply函数和 * 运算符完成矩阵的点乘，使用matmul函数，np.dot()  和@运算符完成矩阵的叉乘。

import numpy as npA=np.array([[1,0],[0,1]])
B=np.array([[1,1],[1,1]])
print("两个2维矩阵的乘法:")#A*B 的结果是对应元素相乘
C=A*B
print(f"A*B=\n{C}")#np.multiply 的结果是对应元素相乘
C=np.multiply(A,B)
print(f"np.mutliply(A,B)=\n{C}")#np.dot  矩阵的np.dot结果是不是点积，而是叉积！
C=np.dot(A,B)
print(f"C=np.dot(A,B)=\n{C}")#np.matmu 的结果是叉积
C=np.matmul(A,B)
print(f"np.matmul=\n{C}")#A @ B 的结果是叉积
C=A @ B
print(f"A @ B=\n{C}")#np.cross 的结果是？
C=np.cross(A,B)
print(f"np.cross=\n{C}")

两个2维矩阵的乘法:
A*B=
[[1 0][0 1]]
np.mutliply(A,B)=
[[1 0][0 1]]
C=np.dot(A,B)=
[[1 1][1 1]]
np.matmul=
[[1 1][1 1]]
A @ B=
[[1 1][1 1]]
np.cross=
[ 1 -1]

4.2.2  关于2个3*3矩阵的点乘和叉乘

• 和2维向量计算基本相同

import numpy as npA=np.array([[1,0,0],[0,1,0],[0,0,1]])
B=np.array([[1,1,1],[1,1,1],[1,1,1]])
print("两个3维矩阵的乘法:")#A*B 的结果是对应元素相乘
C=A*B
print(f"A*B=\n{C}")#np.multiply 的结果是对应元素相乘
C=np.multiply(A,B)
print(f"np.mutliply(A,B)=\n{C}")#np.dot  矩阵的np.dot结果是不是点积，而是叉积！
C=np.dot(A,B)
print(f"C=np.dot(A,B)=\n{C}")#np.matmu 的结果是叉积
C=np.matmul(A,B)
print(f"np.matmul=\n{C}")#A @ B 的结果是叉积
C=A @ B
print(f"A @ B=\n{C}")#np.cross 的结果是？
C=np.cross(A,B)
print(f"np.cross=\n{C}")

两个3维矩阵的乘法:
A*B=
[[1 0 0][0 1 0][0 0 1]]
np.mutliply(A,B)=
[[1 0 0][0 1 0][0 0 1]]
C=np.dot(A,B)=
[[1 1 1][1 1 1][1 1 1]]
np.matmul=
[[1 1 1][1 1 1][1 1 1]]
A @ B=
[[1 1 1][1 1 1][1 1 1]]
np.cross=
[[ 0 -1  1][ 1  0 -1][-1  1  0]]

4.3 如果矩阵*向量呢？

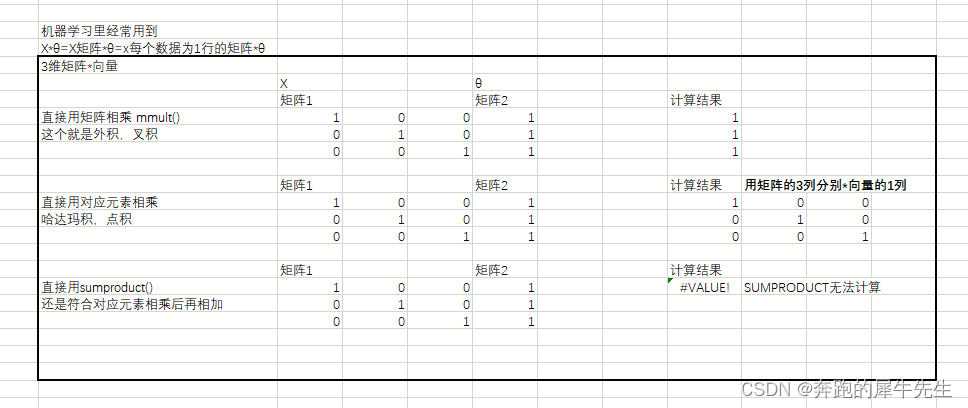
4.3.1 用EXCEL计算

• 用EXCEL计算矩阵*向量 基本和 矩阵* 矩阵规则相同
• 除了计算点积，计算哈达玛积，需要用矩阵的每1列*向量的列

4.3.2 用python计算

• 和矩阵*矩阵的类似
• python里，矩阵的点积则是，A*B 或者np.multiply(A,B)
• python里，矩阵的叉积则是，np.dot(A,B) ,np.matmul() 或则 A@B

import numpy as npA=np.array([[1,0,0],[0,1,0],[0,0,1]])
B=np.array([1,1,1])
print("3维矩阵*向量的乘法:")#A*B 的结果是对应元素相乘
C=A*B
print(f"A*B=\n{C}")#np.multiply 的结果是对应元素相乘
C=np.multiply(A,B)
print(f"np.mutliply(A,B)=\n{C}")#np.dot  矩阵的np.dot结果是不是点积，而是叉积！
C=np.dot(A,B)
print(f"C=np.dot(A,B)=\n{C}")#np.matmu 的结果是叉积
C=np.matmul(A,B)
print(f"np.matmul=\n{C}")#A @ B 的结果是叉积
C=A @ B
print(f"A @ B=\n{C}")#np.cross 的结果是？
C=np.cross(A,B)
print(f"np.cross=\n{C}")

3维矩阵*向量的乘法:
A*B=
[[1 0 0][0 1 0][0 0 1]]
np.mutliply(A,B)=
[[1 0 0][0 1 0][0 0 1]]
C=np.dot(A,B)=
[1 1 1]
np.matmul=
[1 1 1]
A @ B=
[1 1 1]
np.cross=
[[ 0 -1  1][ 1  0 -1][-1  1  0]]

5 点积和叉积的数学计算总结

5.1 点积计算

• 点积计算
• 点积，就是内积，就是哈达玛积
• 计算方法

5.1.1 如果是向量的点积

1. 如果是向量，就用对应元素相乘后再求和为标量。
2. EXCEL里用sumproduct()，或者mmult(行向量，列向量)
3. 而python里可以用 np.dot(A,B) ,
4. 如果python利用的是 A*B 或者 np.multiply(A,B) 会得到向量，所以则需要再把得到的向量，直接多元素求和的结果才是点积。

5.1.2 如果是矩阵的点积

1. 如果是矩阵，就直接用对应元素相乘后形成的新矩阵即可，不需要再算标量！
2. EXCEL直接，A，B如果是同型矩阵，则对应元素相乘即可。
3. python里，不能用np.dot，而要用A*B 或者 np.multiply(A,B) 会得到点积，不需要再求和处理。

5.2 叉积计算

• 叉积就是外积

5.2.1 向量的的叉积计算

1. 如果是向量，就用对应元素相乘后再求和为标量。
2. EXCEL里只能套用公式计算叉积
3. c = a×b = (y1*z2-y2*z1 , x2*z1-x1*z2 , x1*y2-x2*y1)
4. python里可以用np.cross(A,B) 计算叉积

5.2.2 矩阵的叉积计算

1. 如果是居住的叉积计算
2. EXCEL里直接用mmult(矩阵，矩阵) 即可
3. 而python里可以用 np.dot(A,B) ,np.matmul() 或则 A@B计算叉积
4. np.cross() 算出来的是个啥？暂时不知道了？

5.3 向量的点积，叉积

• EXCEL里，向量的点积就是 sumproduct() 或者mmult(行向量，列向量)
• EXCEL里，向量的点叉积只能套公式计算c = a×b = (y1*z2-y2*z1 , x2*z1-x1*z2 , x1*y2-x2*y1)
• python里，向量的点积，就是np.dot(A,B)
• python里，向量的叉积，就是np.cross(A,B)

5.4 矩阵的点积，叉积

• EXCEL里，矩阵的点积直接用对应元素相乘
• EXCEL里，矩阵的叉积直接用 mmult(A,B)
• python里，矩阵的点积则是，A*B 或者np.multiply(A,B)
• python里，矩阵的叉积则是，np.dot(A,B) ,np.matmul() 或则 A@B