这篇文章将尝试推导扩散模型 DDPM 中涉及公式,主要参考两个 B 站视频:
- 大白话AI
- 狗中赤兔
本文所用 PPT 元素均来自 UP 主,狗中赤兔和大白兔AI,特此感谢。
在证明开始,我们需要先对扩散模型有一个整体的认知。扩散模型通常由①前向的加噪过程②逆向的去噪过程构成。如下图所示:

从左到右是 加噪过程,从右到左是 去噪过程。
我们在上一篇文章中,已经像大家介绍了扩散模型的基本原理(这篇)
我们通过简单的表征模块搭建简单的去噪模型,在 MNIST 手写体数据集上搭建了多步去噪模型。相信上述 demo 可以帮助大家理解扩散模型主要工作流程。这篇文章,我们将尝试证明其背后的数学原理。
文章目录
- 加噪过程
- 证明什么?
- 证明过程
- 去噪过程
- 证明什么?
- 证明过程
- 训练过程
加噪过程
证明什么?
扩散模型加噪过程就是从原始图片开始,逐步向其中添加噪声,直至图片完全模糊。我们首先使用数学公式表述这一过程。
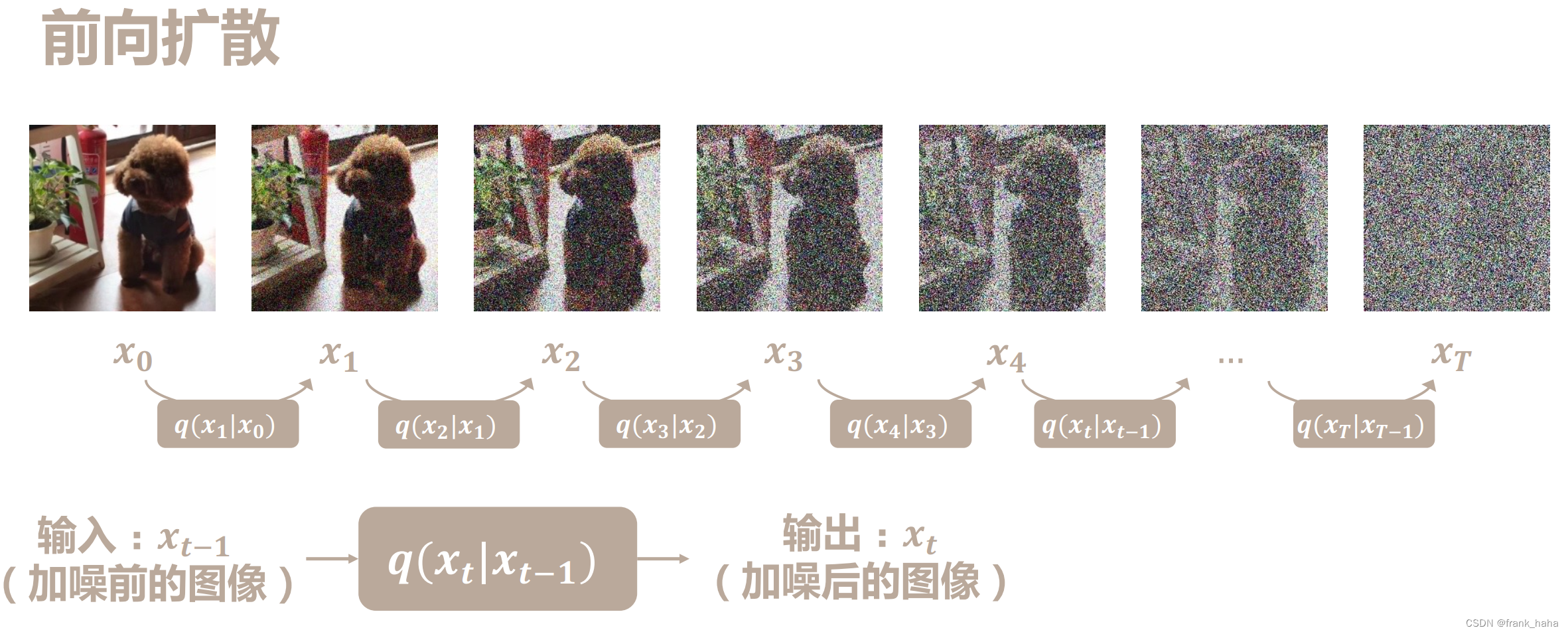
汇总一下已知的条件:
- 扩散过程符合马尔科夫随机过程,每一步均仅和上一步有关
q ( x t ∣ x t − 1 ) = N ( 1 − β t x t − 1 , β t I ) q(x_t|x_{t-1})=\mathcal{N}(\sqrt{1-\beta_t}x_{t-1},\beta_t I) q(xt∣xt−1)=N(1−βtxt−1,βtI) - 每一步中添加的噪声均是从高斯分布中抽取的随机数,即
x t = 1 − β t x t − 1 + β t ⋅ ϵ x_t=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}\cdot\epsilon xt=1−βtxt−1+βt⋅ϵ
注意,噪声和源图片是掺杂的状态,掺杂比例平方和是 1,大家可以到 这个网站 感受一下。
我们已经知道了前向过程是一个马尔科夫链,并知道了每一步添加的噪声服从高斯分布。那么,是否有可能从最开始原始状态直接加噪到特定时间步所处状态呢?即,证明, q ( x t ∣ x 0 ) = N ( C t 2 x 0 , C t 1 I ) q(x_t|x_{0})=\mathcal{N}(C_{t2}x_{0},C_{t1} I) q(xt∣x0)=N(Ct2x0,Ct1I)
x t = C t 2 x 0 + C t 1 ⋅ ϵ x_t=C_{t2}x_{0}+C_{t1}\cdot\epsilon xt=Ct2x0+Ct1⋅ϵ
证明过程
首先,我们定义两个马尔科夫链,然后将式2带入式1,并进行化简。注意到,两个随机噪声可以进行合并,这里运用了高斯分布两个特殊性质:
- 一个随机数是从标准高斯分布中采样得到的,对这个随机数乘以一个不为零的常数,相乘结果依然是高斯分布

- 两个随机数分别从两个独立高斯分布中抽取得到,两数相加所得结果依然服从高斯分布

详细证明过程如下:

上述证明结果表示,任一时间步的加噪状态可以由初始照片通过一步加噪得到。注意到,加噪过程是不涉及神经网络的,不需要进行网络训练。此外,我们的 α ‾ t \overline{\alpha}_{t} αt 是由 α 1 α 2 … α t \alpha_{1}\alpha_{2}\dots\alpha_{t} α1α2…αt 连乘得到的。这些数均是小于 1 的正数,所以当扩散步数足够多时, x t x_t xt 将被噪声淹没,变成一张完全遵从高斯分布的噪声。
去噪过程
证明什么?
在上一篇文章中,我们实现了多步迭代去噪模型。该模型可看作扩散模型的原型,简单直接的展示了扩散模型的主要工作原理。但是在真实的扩散模型设计中,逆向去噪会更加复杂一些。如下图所示:
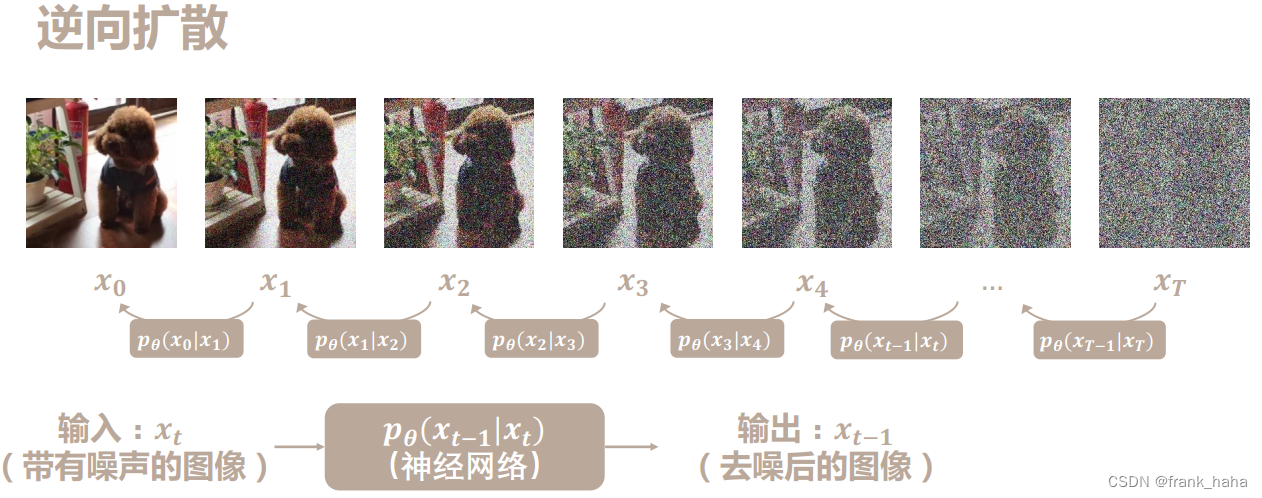
我们希望以加噪图片为输入,让模型预测所加噪声或者去噪后的图像,用数学表达式表示则为:
p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_{t}) pθ(xt−1∣xt)
既然要训练神经网络拟合这一分布,那么,一个很自然的问题是,这一分布的表达式是什么?
为了回答这一问题,我们首先汇总一下已知条件:
- 去噪过程遵循马尔科夫过程,每一步去噪只与当前状态有关
- 由上一小节可得,每一步加噪状态均可由原始图像通过一步加噪得到
下面,我们将尝试回答神经网络需要拟合的表达式是什么?
证明过程
在开始之前,我们先来复习下贝叶斯定理
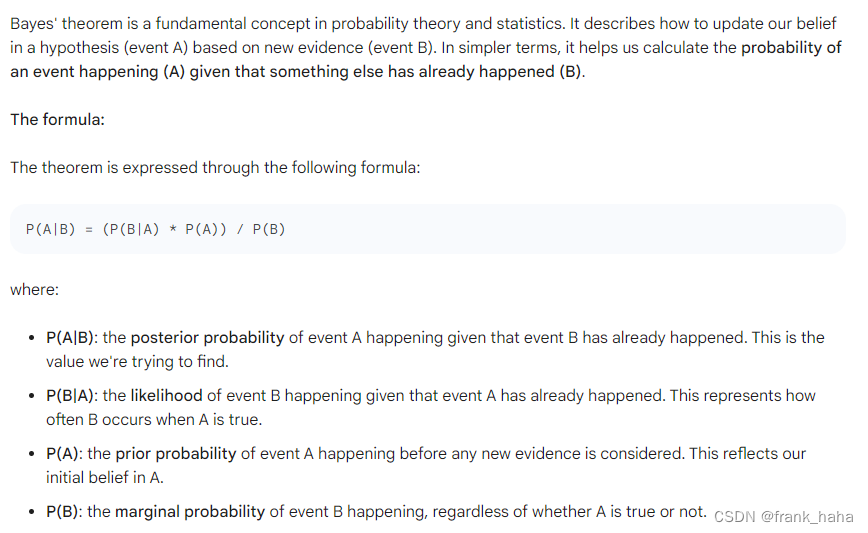
贝叶斯定理的好处是,可以将复杂概率问题拆分成已知的简单概率问题的组合。
上述将要求解的 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_{t}) p(xt−1∣xt)可以使用贝叶斯定理进行化简:
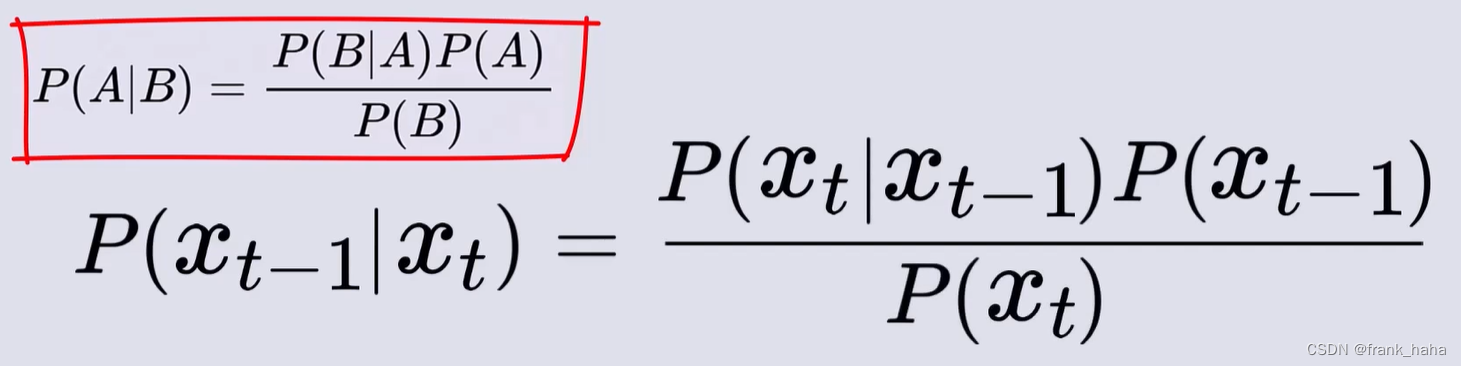
进一步的,我们可以给式中各项添加 x 0 x_0 x0
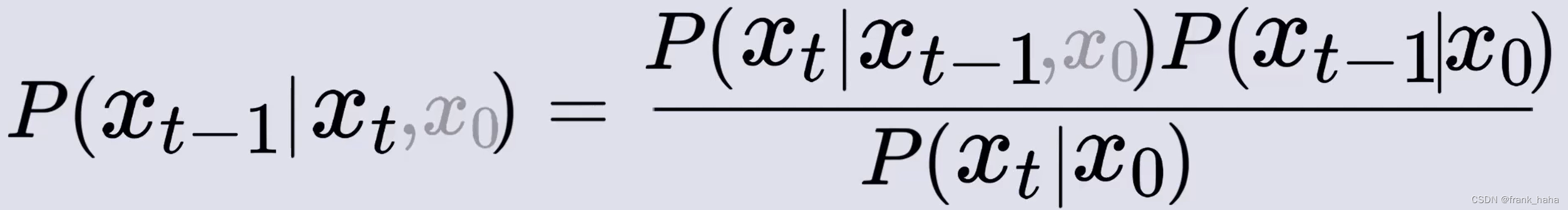
此处左式和右式左上方中的 x 0 x_0 x0 可以近似忽略,现在我们将注意力放在等式右边的三个表达式上。
在上一节中,我们证明了,①任意时间步的带噪图像均可由原始图像一步加噪得到,这一噪声符合高斯分布;②任意时间步的带噪图像可由前一步图像加噪得到,这一噪声也符合高斯分布。这两点用公式表示如下:
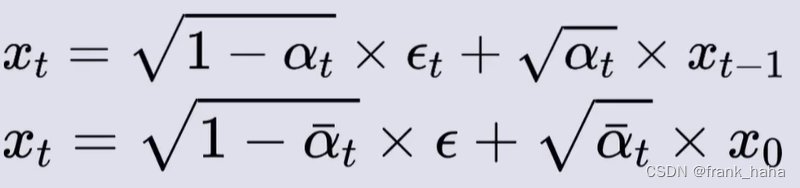
等式右边的三个表达式可通过上述两个公式(及其一个拓展)得到,因为理论上,上两式是对一个来自高斯分布的随机数进行线性变换,所以变换结果也应遵从高斯分布:
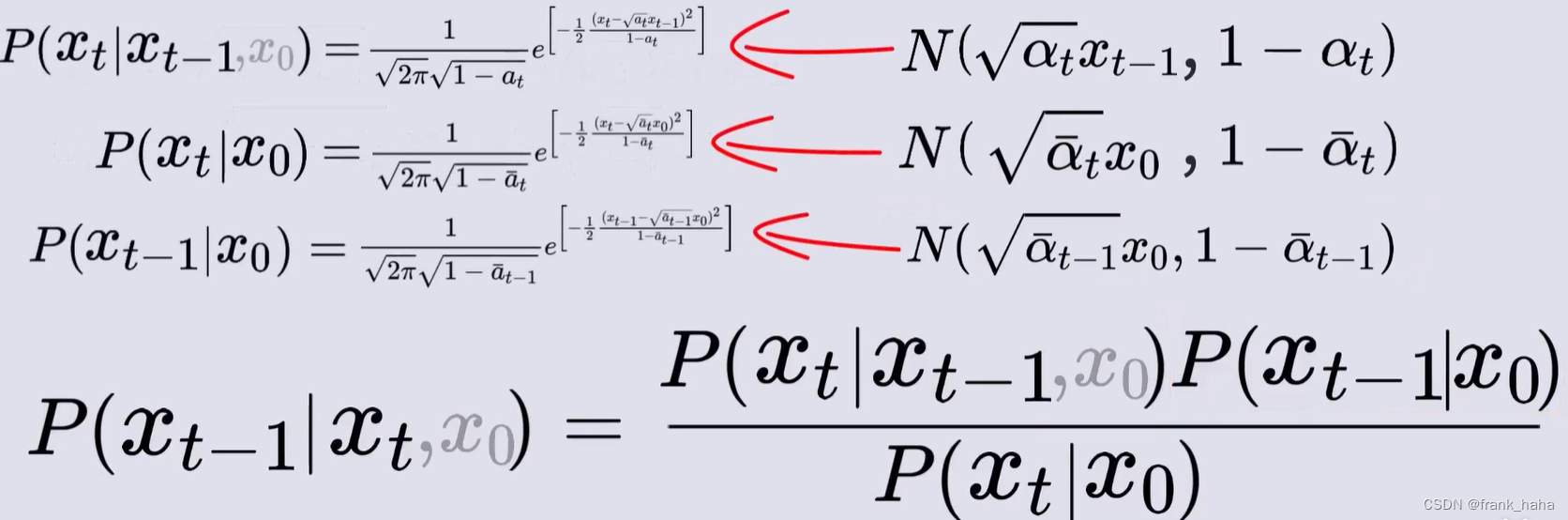
下面就是将右式中的三个表达式代入高斯分布下的表达,并进行合并化简。
化简过程十分复杂,我们只需要知道能化简,而且化简结果也是一个高斯分布:
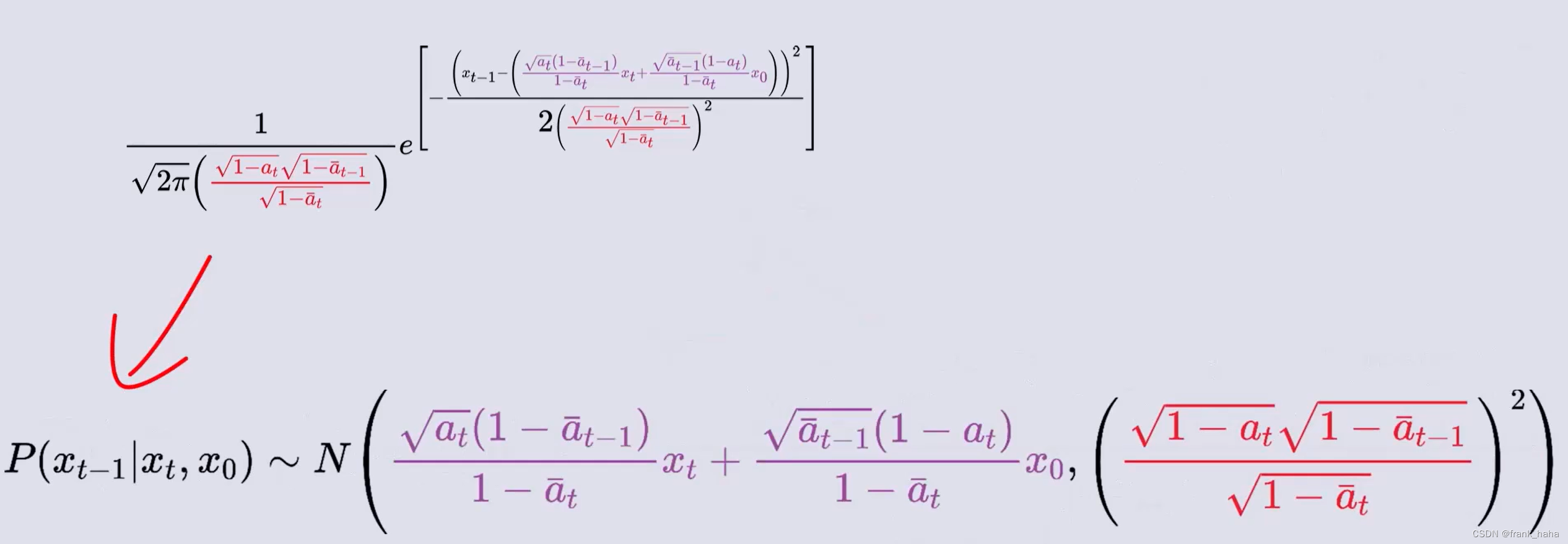
再回头看:

我们的逆向过程是希望在已知 x T x_T xT(which is a 高斯噪声)的情况下,通过去噪神经网络一步步倒推回去,得到 x 0 x_0 x0
我们经过复杂推导,得到了神经网络的表达式
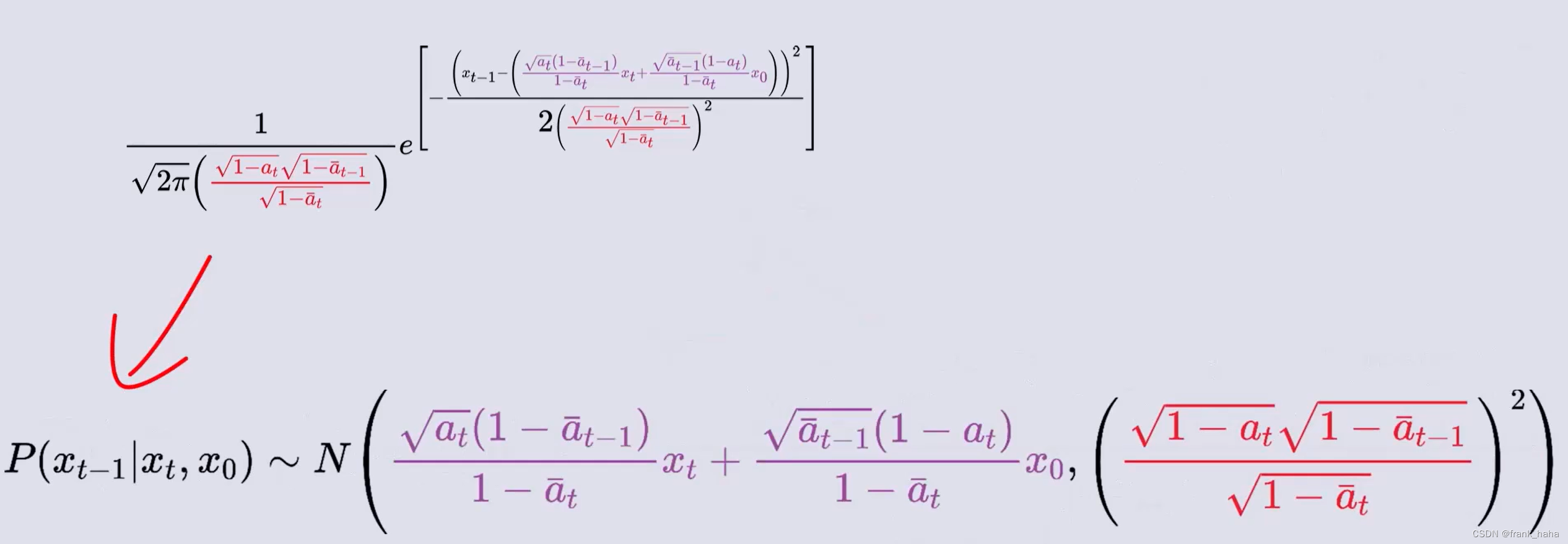
但该表达式中,含有我们想要求解的 x 0 x_0 x0,所以我们需要进一步将 x 0 x_0 x0 替换掉
我们对上一节证明的, x 0 x_0 x0 和 x T x_T xT 之间的关系式进行变形,代入主表达式:
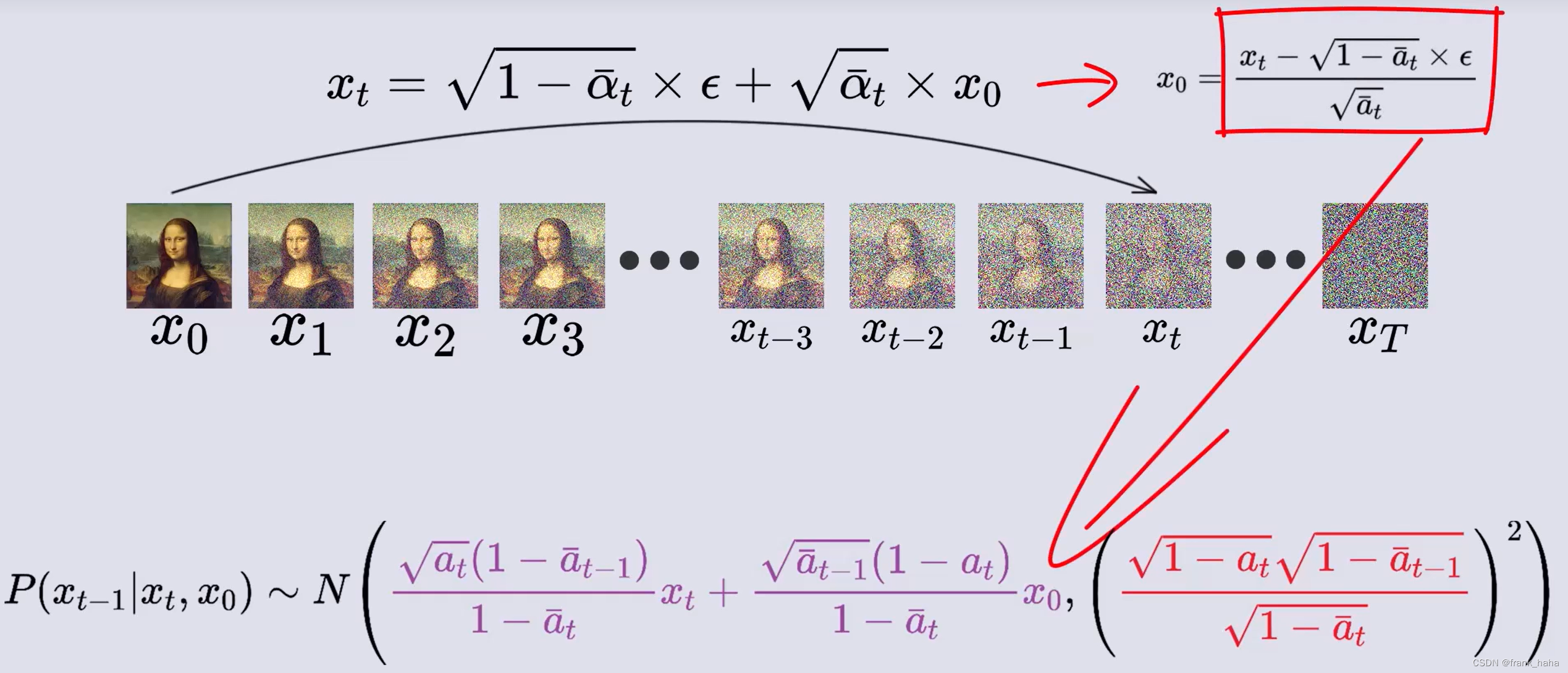
化简得到最终结果:
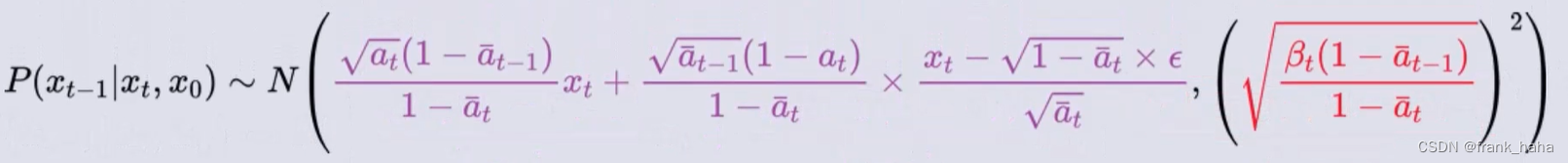
此时,我们终于有了一个 “知道 x t x_t xt 值即可求得 x t − 1 x_{t-1} xt−1 值的关系式” 了。这个关系式就是我们所谓的去噪网络
但是,注意到,该关系式并不是一个确定的概率分布,其中还有一个随机数 ϵ \epsilon ϵ 。当这个随机数确定的时候,我们才能真正敲定该概率分布。
众所周知,神经网络是黑箱拟合一切难题的法宝,所以我们将预测随机数的任务就交给神经网络。
公式推导到这里,所谓去噪网络的功能发生了一点点变化。一开始,我们的想法是,输入带噪图像,输出干净图片:

现在变成了,输入带噪图像,预测噪声 ϵ \epsilon ϵ ,将该噪声代入表达式:
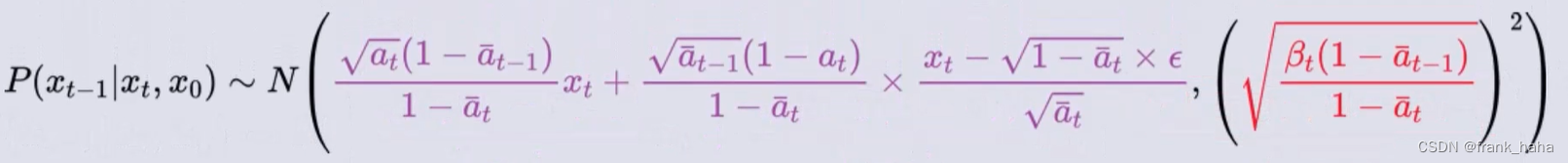
得到基于带噪图片向前推理的概率分布,最后,我们再从该分布中抽取一张图片。逻辑链如下所示:
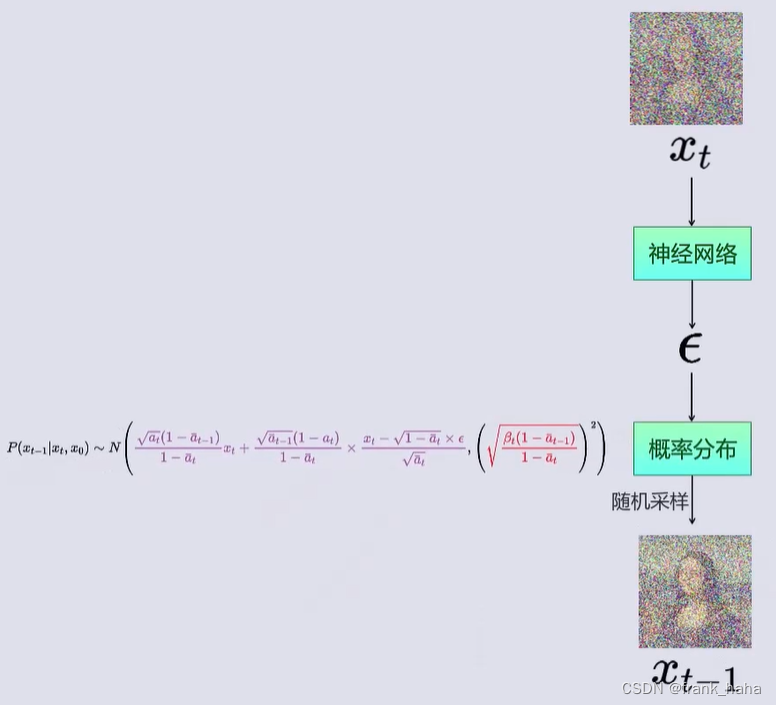
最后遗留的小问题:去噪过程最开始,如何拿到 x T x_T xT 呢?在上一小节末尾,我们提到,当一个照片加噪次数足够多时,带噪图片将变成一张高斯噪声。因此,我们将随机高斯噪声作为 x T x_T xT 即可。
训练过程
写到这里,相信大多数读者都和我一样感到疲惫,但事实上,扩散模型最难的理论部分才刚刚开始。这一部分在下面两个视频中有讲解:
- 狗中赤兔
- 梗直哥
此处仅放出训练神经网络的误差函数:
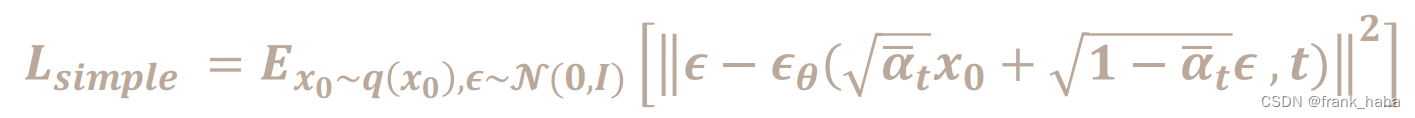
其中 ϵ θ \epsilon_{\theta} ϵθ 是神经网络预测的噪声, ϵ \epsilon ϵ 是服从高斯分布的随机噪声(真实噪声),t 是时间步
将上述几个变量代入误差函数即可得到神经网络真正的优化目标。
希望读到这里的读者能锲而不舍,继续推导相关公式,俺退了,祝好!