2846. 边权重均等查询

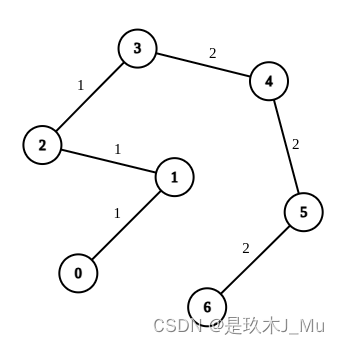
输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出：[0,0,1,3]
解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。
第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。
第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

分析

如果暴力写的话， 那么对于每一个查询，我们要dfs一遍，每一遍存一下路径上的边权得数量，最后用总的数量减去最多的变得数量就是答案，这是一个小贪心的思路，那么考虑一下数据范围，如果暴力写的话，时间复杂度是$O(n^2)$，肯定会超时的，但是也吧暴力写法的代码贴出来。

723 / 733 个通过的测试用例

暴力 dfs （会超时）

class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {int m = queries.size();vector<int> e(n << 1), ne(n << 1), h(n, -1), w(n << 1), ans(m); // 链式向前星int cnt[27], idx = 0;// addfunction<void(int, int, int)> add = [&](int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;e[idx] = a, ne[idx] = h[b], w[idx] = c, h[b] = idx ++;}; // add// dfsfunction<bool(int, int, int)> dfs = [&](int u, int b, int fa) {if (u == b) {return true;}for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (j == fa) continue;if (dfs(j, b, u)) {++ cnt[w[i]];return true;}}return false;}; // dfsfor (int i = 0; i < n - 1; i ++ ) {int a = edges[i][0], b = edges[i][1], w = edges[i][2];add(a, b, w);}for (int i = 0; i < m; i ++) {memset(cnt, 0, sizeof cnt); // 每次清空数组int a = queries[i][0], b = queries[i][1];dfs(a, b, -1);int res = 0, sum = 0;for (int i = 1; i <= 26; i ++) {sum += cnt[i];res = max(res, cnt[i]);}ans[i] = sum - res;}return ans;}
};

时间复杂度：$O(n\ast m\ast W)$ (本题 W = 26)

分析

我们可以用最近公共祖先的思想，选定一个根节点，假设是0，那么定义一个cnt[i][w]表示节点i到根节点的路径中边权为w(1 <= w <= 26)的边的数量，那么i到j之间边权为w的边数是$t_a=cnt[i][w]+cnt[j][w]-2\ast cnt[lca(i,j)][w]$，lca(i, j)表示节点i和节点j的最近公共祖先, 那么要替换的边数就是
$$\sum _{i=1}^{26}{t}_i-\underset{1<=i<=26}{\max }{t}_i$$
使用离线算法tarjan算法模板

tarjan + 并查集

class Solution {
public:using PII = pair<int, int>;vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {int m = queries.size();vector<unordered_map<int, int>> g(n);for (auto& e : edges) {g[e[0]][e[1]] = e[2];g[e[1]][e[0]] = e[2];}vector<vector<PII>> q(n);   for (int i = 0; i < m; i ++ ){q[queries[i][0]].push_back({queries[i][1], i});q[queries[i][1]].push_back({queries[i][0], i});}vector<int> lca(m), vis(n), p(n);iota(p.begin(), p.end(), 0);vector<vector<int>> cnt(n, vector<int>(27));function<int(int)> find = [&](int x) {if (x != p[x]) p[x] = find(p[x]);return p[x];};function<void(int, int)> tarjan = [&](int u, int fa) {if (fa != -1) {cnt[u] = cnt[fa];++ cnt[u][g[u][fa]];}p[u] = u;for (auto& e : g[u]) {if (e.first == fa) continue;tarjan(e.first, u);p[e.first] = u;}for (auto& e : q[u]) {if (u != e.first && !vis[e.first]) continue;lca[e.second] = find(e.first);}vis[u] = 1;};tarjan(0, -1);vector<int> res(m);for (int i = 0; i < m; i ++ ){int sum = 0, mx = 0;for (int j = 1; j <= 26;j ++) {int t = cnt[queries[i][0]][j] + cnt[queries[i][1]][j] - 2 * cnt[lca[i]][j];mx = max(mx, t);sum += t;}res[i] = sum - mx;}return res;}
};

时间复杂度：$O((m+n)\times W+m\times logn)$ (本题 W = 26)

在线lca算法

const int N = 10010;
class Solution {
public:int e[N << 1], ne[N << 1], w[N << 1], h[N],  idx;int fa[N][15], depth[N];int cnt[N][27], cntn[27];int q[N];void bfs() {int hh = 0, tt = 0;q[0] = 1;memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;while (hh <= tt) {int t = q[hh ++ ];for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;q[ ++ tt] = j;fa[j][0] = t;for (int k = 1; k <= 14; k ++ )fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}}// dfs版本void dfs_dep(int u, int father) {depth[u] = depth[father] + 1;fa[u][0] = father;for (int i = 1; i <= 14; i ++) fa[u][i] = fa[fa[u][i - 1]][i - 1];for (int i = h[u]; ~i; i = ne[i]) {if (e[i] != father) {dfs_dep(e[i], u);}}}void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;}void dfs(int u, int fa) {memcpy(cnt[u], cntn, sizeof cntn);for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (fa == j) continue;cntn[w[i]] ++;dfs(j, u);cntn[w[i]] -- ;}}int lca(int a, int b){if (depth[a] < depth[b]) swap(a, b);for (int k = 14; k >= 0; k -- )if (depth[fa[a][k]] >= depth[b]) a = fa[a][k];if (a == b) return a;for (int k = 14; k >= 0; k -- ) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];}vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {memset(h, -1,sizeof h);for (int i = 0; i < edges.size(); i ++ ) {int a = edges[i][0], b = edges[i][1], c = edges[i][2];a ++, b ++ ;add(a, b, c), add(b, a, c);}bfs();// dfs_dep(1, 0); // dfs_dep版本dfs(1, -1);vector<int> ans(queries.size());for (int i = 0; i < queries.size(); i ++ ) {int a = queries[i][0], b = queries[i][1];a ++, b ++ ;int p = lca(a, b);vector<int> s(27);for (int j = 1; j <= 26; j ++ )s[j] += cnt[a][j] + cnt[b][j] - cnt[p][j] * 2;int sum = 0, maxv = 0;for (int j = 1; j <= 26; j ++ ) {maxv = max(maxv, s[j]);sum += s[j];}ans[i] = sum - maxv;}return ans;}
};

时间复杂度：$O(mlogn)$