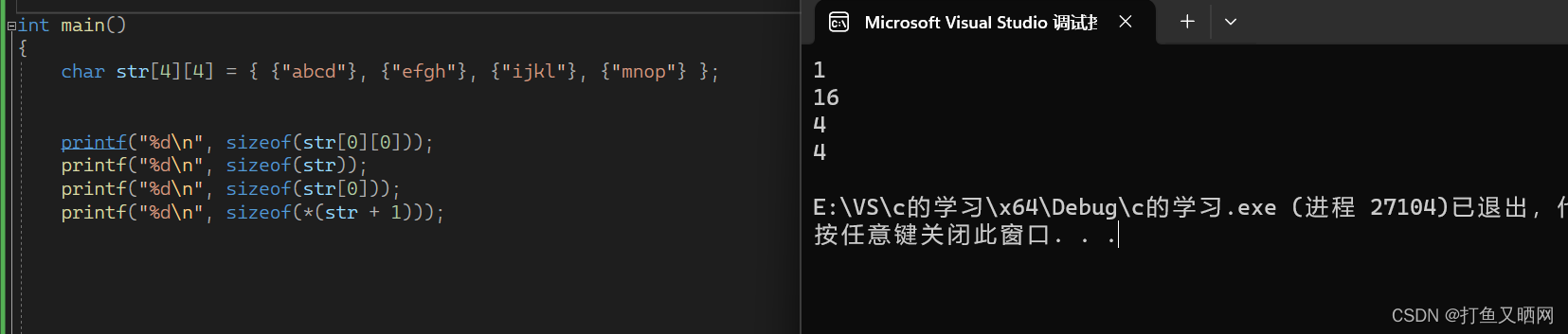
思路：

本题的本质是树的dfs， 每次dfs可以确定以u为重心的最大连通块的节点数，并且更新一下ans。

也就是说，dfs并不直接返回答案，而是在每次更新中迭代一次答案。

这样的套路会经常用到，在 树的dfs 题目中

总结以u为根的子树个数可由dfs（j）不断递归得到

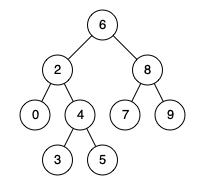
 由于本题给出的图是无向图，假如首次遍历，不论取那个节点，它都会把与他联通的所有子树全部加入sum，最终sum都==n。

例如从4开始遍历的话，上面一块和下面两块连通块数目都被计算过并被加到sum中。

循环结束后sum==n,没必要取res=max(res,n-sum)。

res=max(n-sum,res)对于首次遍历的节点来说是确实没必要的；但对后续的子节点dfs时由于其父节点已经遍历过了，for循环中就不能获取到以父节点为根的子树。

比如节点4，sum就只能取到节点4下面的两个子树节点数之和，取不到它的父节点，这种情况就需要max(n-sum,res)，n-sum指的是去除下面的两个子树节点数，该树还剩下的节点数。

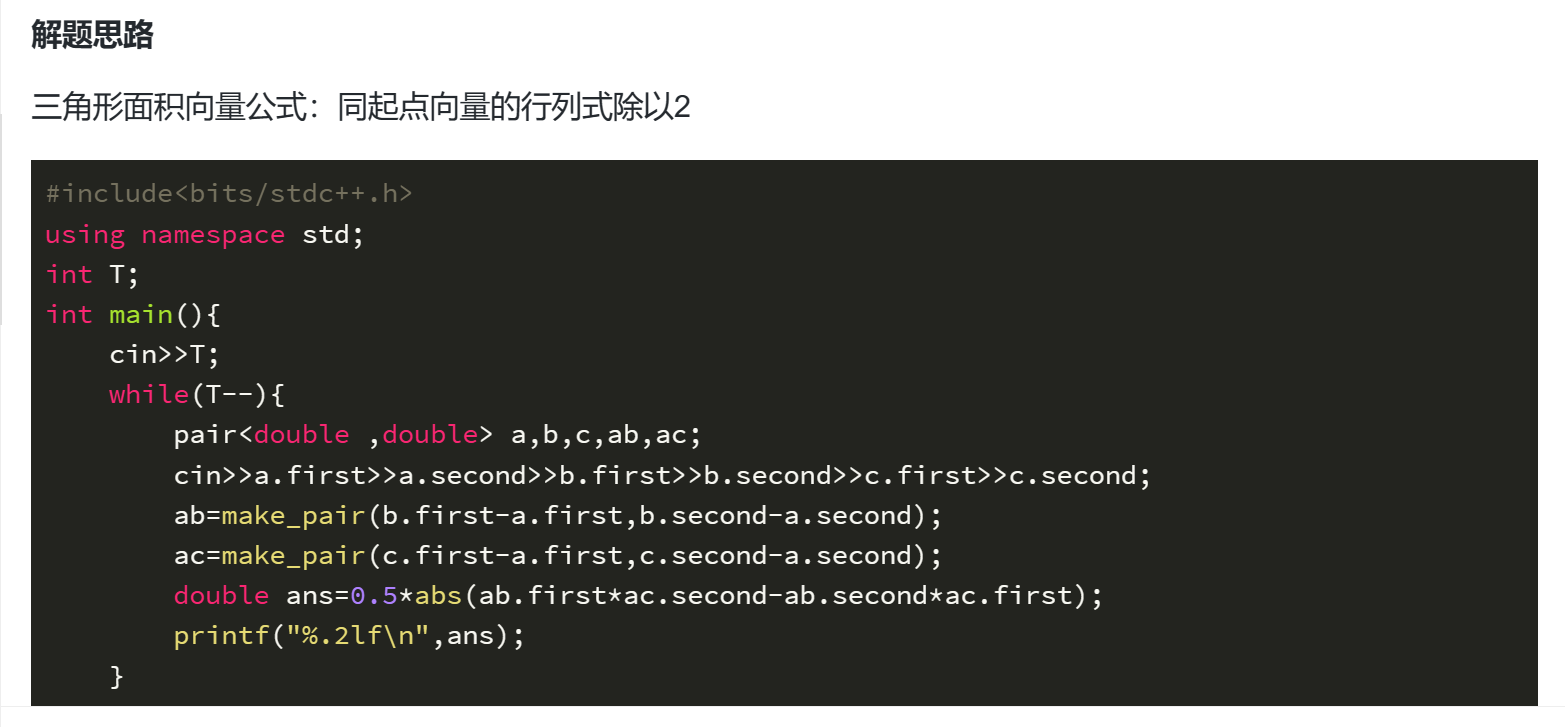
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int e[N], h[N*2], ne[N*2], idx; //无向图最多开2 * N条边 bool st[N]; //用于记录每个结点是否被访问
int n;
int ans = N;
void insert(int a,int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
int dfs(int u)
{st[u] = true; //标记已经搜过了int sum = 1,res = 0;  //res记录以当前节点为重心所有连通块节点数的最大值 ，sum记录以当前点为根节点的子树节点数 ，初始值为1for (int i = h[u]; i != -1; i=ne[i])//for循环遍历每个树节点所有与之相连的节点{int k = e[i]; //获取结点if (!st[k])  //如果这个结点没有被搜过{int s = dfs(k); //深搜获取每个连通块结点个数res = max(res, s); sum += s;}}res = max(res, n - sum);ans = min(ans, res);return sum;
}
int main()
{cin >> n;memset(h, -1, sizeof h);int a, b;for(int i=1;i<n;i++){cin >> a >> b;insert(a, b);insert(b, a);}dfs(1);cout << ans << endl;
}

算法小白的学习笔记。

图片来源

Acwing846树的重心---------dfs（邻接表）

借鉴了其他大佬的思路。