机器学习-线性回归法

线性回归算法

解决回归问题
思想简单，实现容易
许多强大的非线性模型的基础
结果具有很好的可解释性
蕴含机器学习中的很多重要思想

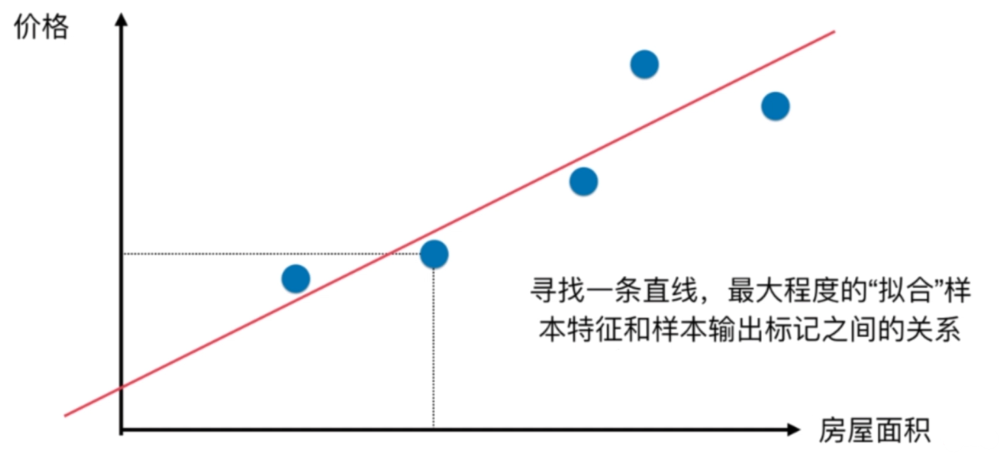
样本特征只有一个，称为：简单线性回归

通过分析问题，确定问题的损失函数或者效用函数
通过最优化损失函数或者效用函数，获得机器学习的模型
几乎所有参数学习算法都是这样的套路

最小二乘法

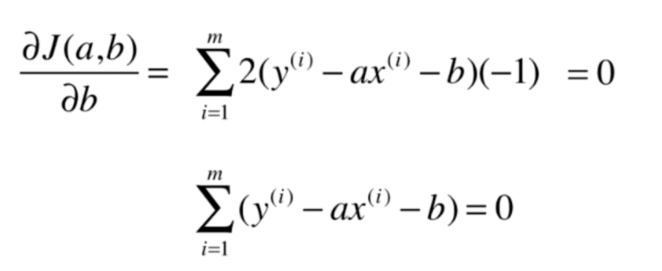
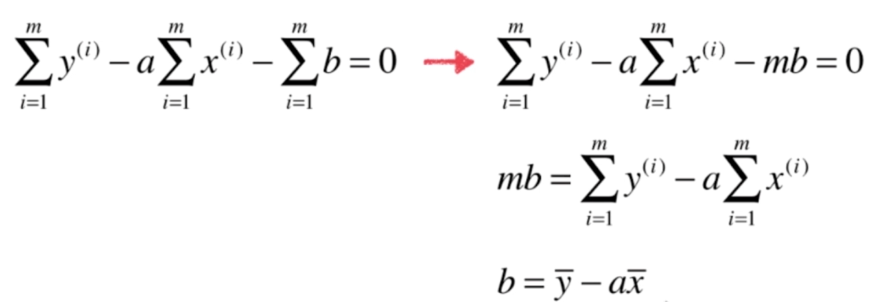
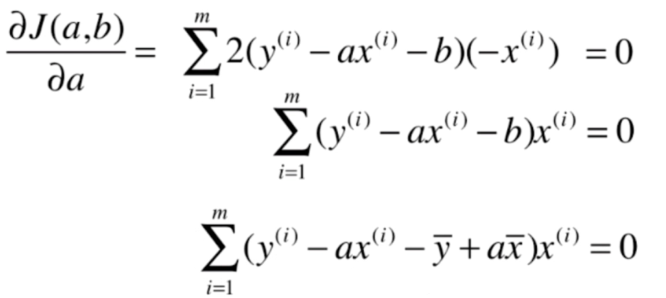
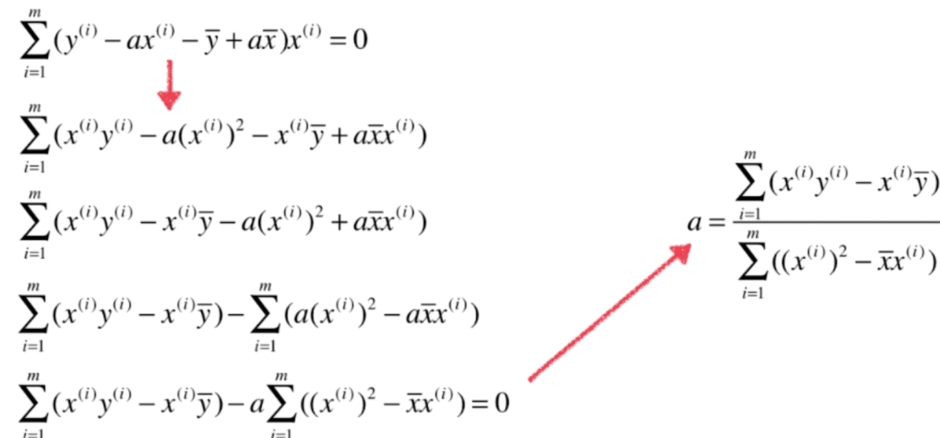
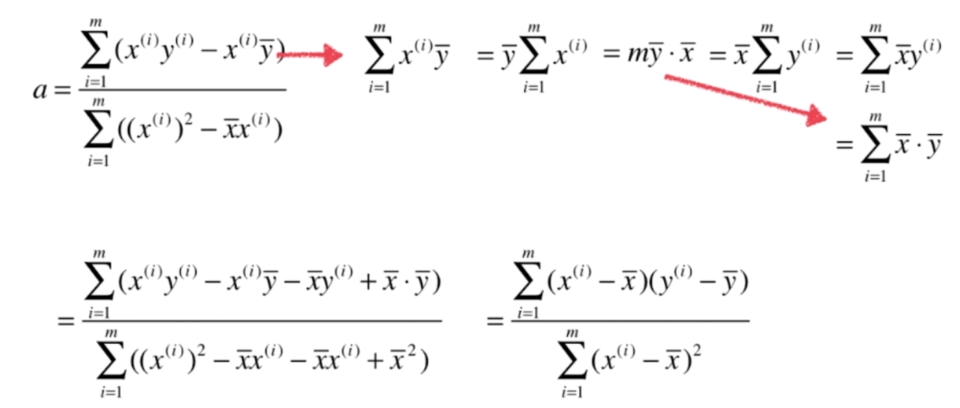
代码实现简单线性回归法

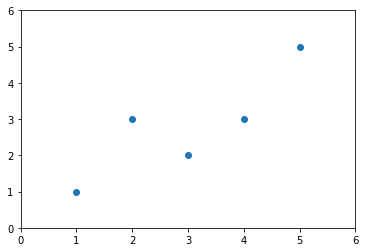
加载数据

import numpy as np
import matplotlib.pyplot as plt
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])
plt.scatter(x, y)
plt.axis([0, 6, 0, 6])
plt.show()

无标题.png
计算过程

x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):num += (x_i - x_mean) * (y_i - y_mean)d += (x_i - x_mean) ** 2a = num/d
b = y_mean - a * x_mean
y_hat = a * x + b

绘图

plt.scatter(x, y)
plt.plot(x, y_hat, color='r')
plt.axis([0, 6, 0, 6])
plt.show()

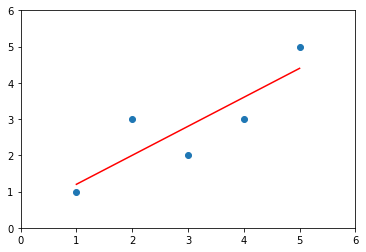
无标题.png
封装我们自己的SimpleLinearRegression

import numpy as npclass SimpleLinearRegression1:def __init__(self):"""初始化Simple Linear Regression 模型"""self.a_ = Noneself.b_ = Nonedef fit(self, x_train, y_train):"""根据训练数据集x_train,y_train训练Simple Linear Regression模型"""assert x_train.ndim == 1, \"Simple Linear Regressor can only solve single feature training data."assert len(x_train) == len(y_train), \"the size of x_train must be equal to the size of y_train"x_mean = np.mean(x_train)y_mean = np.mean(y_train)num = 0.0d = 0.0for x, y in zip(x_train, y_train):num += (x - x_mean) * (y - y_mean)d += (x - x_mean) ** 2self.a_ = num / dself.b_ = y_mean - self.a_ * x_meanreturn selfdef predict(self, x_predict):"""给定待预测数据集x_predict，返回表示x_predict的结果向量"""assert x_predict.ndim == 1, \"Simple Linear Regressor can only solve single feature training data."assert self.a_ is not None and self.b_ is not None, \"must fit before predict!"return np.array([self._predict(x) for x in x_predict])def _predict(self, x_single):"""给定单个待预测数据x，返回x的预测结果值"""return self.a_ * x_single + self.b_def __repr__(self):return "SimpleLinearRegression1()"

向量化运算

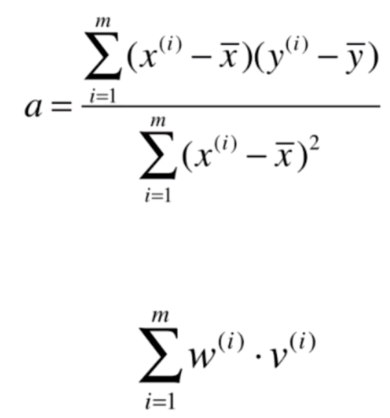
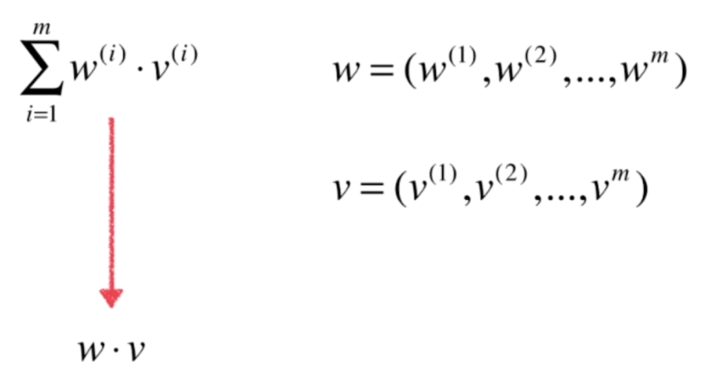
class SimpleLinearRegression2:def __init__(self):"""初始化Simple Linear Regression模型"""self.a_ = Noneself.b_ = Nonedef fit(self, x_train, y_train):"""根据训练数据集x_train,y_train训练Simple Linear Regression模型"""assert x_train.ndim == 1, \"Simple Linear Regressor can only solve single feature training data."assert len(x_train) == len(y_train), \"the size of x_train must be equal to the size of y_train"x_mean = np.mean(x_train)y_mean = np.mean(y_train)self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)self.b_ = y_mean - self.a_ * x_meanreturn selfdef predict(self, x_predict):"""给定待预测数据集x_predict，返回表示x_predict的结果向量"""assert x_predict.ndim == 1, \"Simple Linear Regressor can only solve single feature training data."assert self.a_ is not None and self.b_ is not None, \"must fit before predict!"return np.array([self._predict(x) for x in x_predict])def _predict(self, x_single):"""给定单个待预测数据x_single，返回x_single的预测结果值"""return self.a_ * x_single + self.b_def __repr__(self):return "SimpleLinearRegression2()"

衡量线性回归法的指标：MSE，RMSE和MAE

代码演示
加载波士顿房产数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data[:,5] # 只使用房间数量这个特征
y = boston.target

可视化

plt.scatter(x, y)
plt.show()

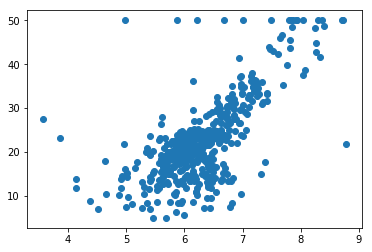
无标题.png
去除最大值

x = x[y < 50.0]
y = y[y < 50.0]
plt.scatter(x, y)
plt.show()

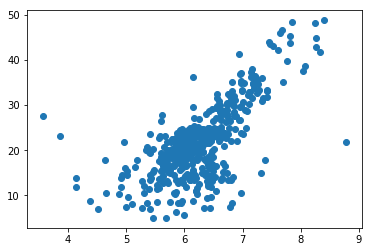
无标题.png
使用简单线性回归法

from playML.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, seed=666)
from playML.SimpleLinearRegression import SimpleLinearRegression
reg = SimpleLinearRegression()
reg.fit(x_train, y_train)
plt.scatter(x_train, y_train)
plt.plot(x_train, reg.predict(x_train), color='r')
plt.show()

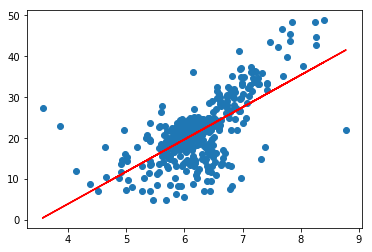
无标题.png
预测

y_predict = reg.predict(x_test)

MSE

mse_test = np.sum((y_predict - y_test)**2) / len(y_test)

RMSE

from math import sqrtrmse_test = sqrt(mse_test)

MAE

mae_test = np.sum(np.absolute(y_predict - y_test))/len(y_test)

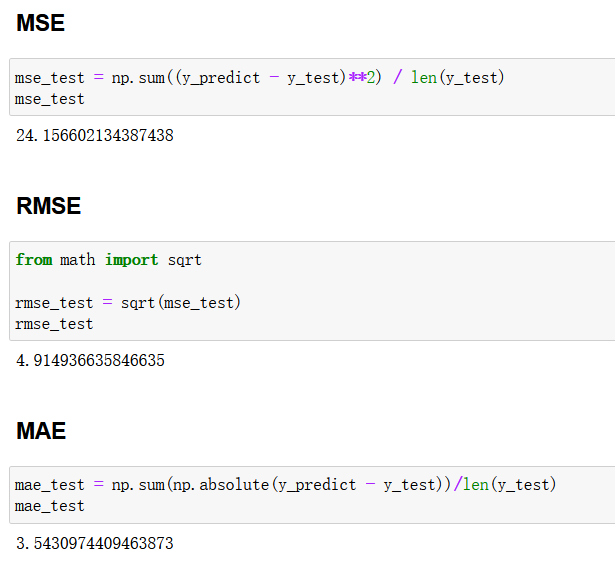
封装

import numpy as np
from math import sqrtdef accuracy_score(y_true, y_predict):"""计算y_true和y_predict之间的准确率"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum(y_true == y_predict) / len(y_true)def mean_squared_error(y_true, y_predict):"""计算y_true和y_predict之间的MSE"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum((y_true - y_predict)**2) / len(y_true)def root_mean_squared_error(y_true, y_predict):"""计算y_true和y_predict之间的RMSE"""return sqrt(mean_squared_error(y_true, y_predict))def mean_absolute_error(y_true, y_predict):"""计算y_true和y_predict之间的MAE"""return np.sum(np.absolute(y_true - y_predict)) / len(y_true)

scikit-learn中的MSE和MAE

from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
mean_squared_error(y_test, y_predict)
mean_absolute_error(y_test, y_predict)

评价回归算法指标：R Square

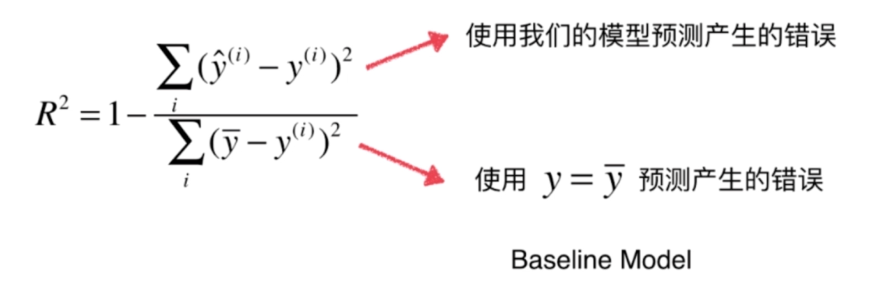
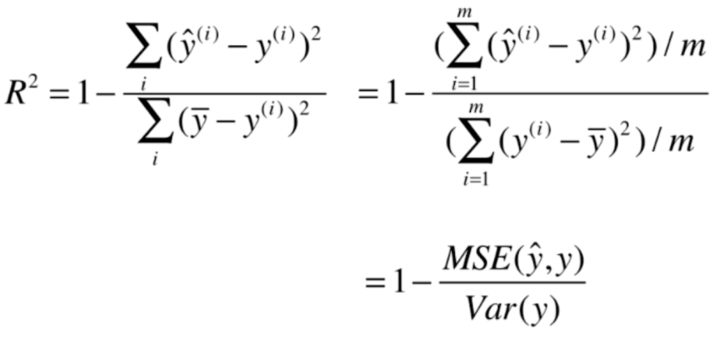
代码

1 - mean_squared_error(y_test, y_predict)/np.var(y_test)

封装

import numpy as np
from math import sqrtdef accuracy_score(y_true, y_predict):"""计算y_true和y_predict之间的准确率"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum(y_true == y_predict) / len(y_true)def mean_squared_error(y_true, y_predict):"""计算y_true和y_predict之间的MSE"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum((y_true - y_predict)**2) / len(y_true)def root_mean_squared_error(y_true, y_predict):"""计算y_true和y_predict之间的RMSE"""return sqrt(mean_squared_error(y_true, y_predict))def mean_absolute_error(y_true, y_predict):"""计算y_true和y_predict之间的MAE"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum(np.absolute(y_true - y_predict)) / len(y_true)def r2_score(y_true, y_predict):"""计算y_true和y_predict之间的R Square"""return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)

scikit-learn中的 r2_score

from sklearn.metrics import r2_scorer2_score(y_test, y_predict)

多元线性回归

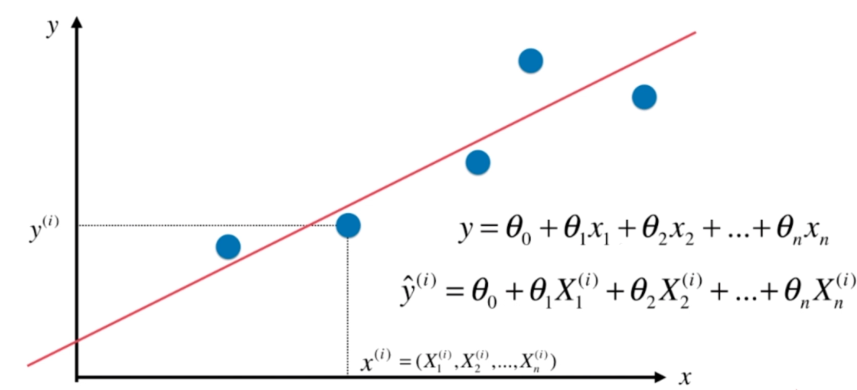
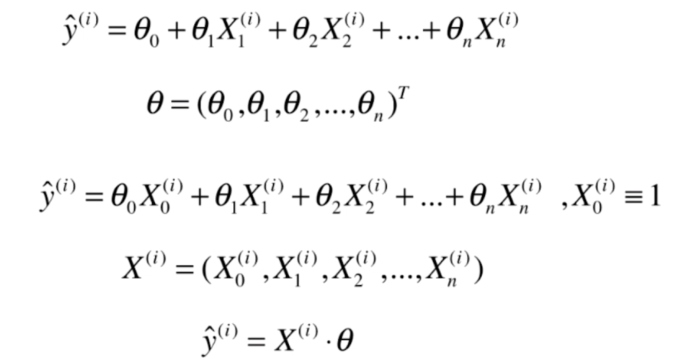
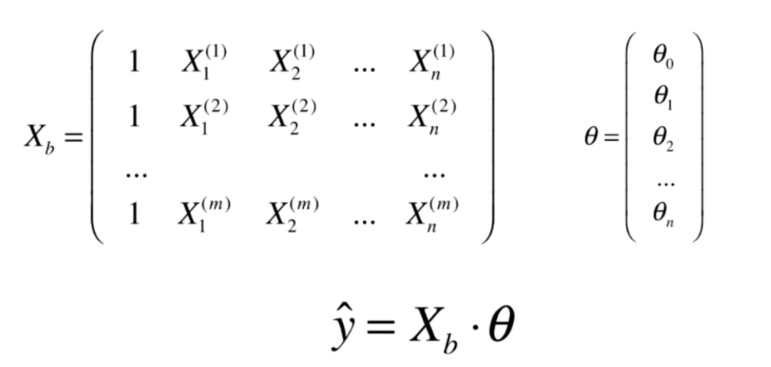
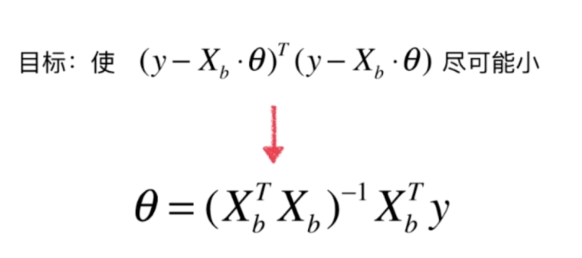
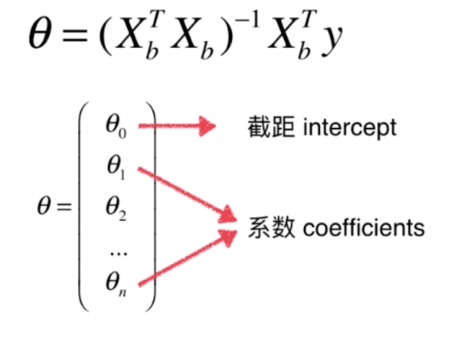
代码实现

import numpy as np
from .metrics import r2_scoreclass LinearRegression:def __init__(self):"""初始化Linear Regression模型"""self.coef_ = Noneself.intercept_ = Noneself._theta = Nonedef fit_normal(self, X_train, y_train):"""根据训练数据集X_train, y_train训练Linear Regression模型"""assert X_train.shape[0] == y_train.shape[0], \"the size of X_train must be equal to the size of y_train"X_b = np.hstack([np.ones((len(X_train), 1)), X_train])self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef predict(self, X_predict):"""给定待预测数据集X_predict，返回表示X_predict的结果向量"""assert self.intercept_ is not None and self.coef_ is not None, \"must fit before predict!"assert X_predict.shape[1] == len(self.coef_), \"the feature number of X_predict must be equal to X_train"X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])return X_b.dot(self._theta)def score(self, X_test, y_test):"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""y_predict = self.predict(X_test)return r2_score(y_test, y_predict)def __repr__(self):return "LinearRegression()"

使用

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()X = boston.data
y = boston.targetX = X[y < 50.0]
y = y[y < 50.0]
from playML.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
from playML.LinearRegression import LinearRegressionreg = LinearRegression()
reg.fit_normal(X_train, y_train)

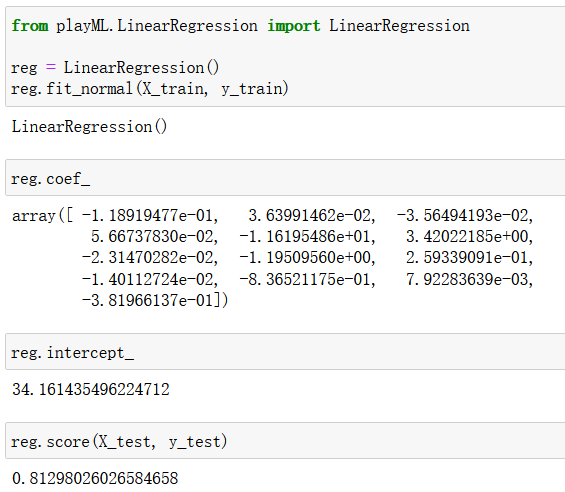
scikit-learn中的线性回归

加载数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()X = boston.data
y = boston.targetX = X[y < 50.0]
y = y[y < 50.0]from playML.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

线性回归

from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)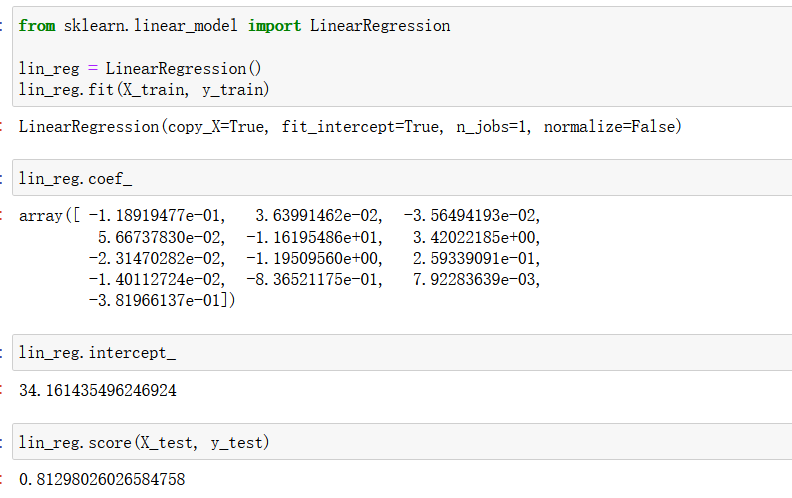

kNN Regressor

from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
knn_reg.score(X_test_standard, y_test)

超参数

from sklearn.model_selection import GridSearchCVparam_grid = [{"weights": ["uniform"],"n_neighbors": [i for i in range(1, 11)]},{"weights": ["distance"],"n_neighbors": [i for i in range(1, 11)],"p": [i for i in range(1,6)]}
]knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)
grid_search.fit(X_train_standard, y_train)