前言
感觉有些题是有难度,但是是我花时间想能想的出来的题目,总体来说做的很爽,题目也不错。个人总结了几个做题技巧,也算是提醒自己。
1.多分类讨论
2.从特殊到一般,便于找规律。例如有一组数,有奇数和偶数,那我们可以构造一组数据全是偶数,观察其规律,然后插入一个奇数,再观察其规律。
3.很多编程题都涉及到数学知识,可以根据题意列出公式,然后试着把这个公式变形,没准有惊喜。
简单题
智乃与瞩目狸猫、幸运水母、月宫龙虾

签到题
void solve() {string s1, s2; cin >> s1 >> s2;int span = 'A' - 'a';if (s1[0] >= 'a' && s1[0] <= 'z') s1[0] += span;if (s2[0] >= 'a' && s2[0] <= 'z') s2[0] += span;if (s1[0] == s2[0]) cout << "Yes" << endl;else cout << "No" << endl;
}智乃的36倍数(easy version)

数据量这么小,暴力就完事。用上atol和c_str函数就行
string s[N];
void solve() {int n; cin >> n;rep(i, 1, n) cin >> s[i];int ans = 0;rep(i, 1, n) {rep(j, i + 1, n) {string t1 = s[i] + s[j];string t2 = s[j] + s[i];int k1 = atol(t1.c_str());int k2 = atol(t2.c_str());if (k1 % 36 == 0)ans++;if (k2 % 36 == 0)ans++;}}cout << ans << endl;
}chino's bubble sort and maximum subarray sum(easy version)

做的时候没看清题目,没关注到k只能是0和1,搞得我想了半天觉得好难,发现了之后就简单多了。
最关键的是怎么球最大字段和,这个一下子就能想到是dp,很经典的题目了。
int a[N], dp[1005];
int n, k;
int ans = -inf;
void check() {//找到最大子段和for (int i = 1; i <= n; i++) {dp[i] = max(dp[i - 1] + a[i], a[i]);ans = max(ans, dp[i]);}}void solve() {cin >> n >> k;rep(i, 1, n) cin >> a[i];if (k == 0) check();else {for (int i = 1; i < n; i++) {swap(a[i], a[i + 1]);check();swap(a[i], a[i + 1]);}}cout << ans << endl;
}中等题
智乃的数字手串


妥妥的诈骗题!!!我总结了以往的诈骗题规律,诈骗题一般都是博弈论(贪心),然后要你输出yes或no,或者让你输出哪个人赢,这种诈骗题代码简单到超乎想象,而且经常是跟判断奇偶性有关。所以我们可以直接去猜答案。
正经分析
首先,偶 = 偶 + 偶 = 奇 + 奇;奇 + 偶 != 偶。
总结一下胜利的条件:(1)拿走最后一个,让对方没得拿 (2)通过交换的操作,使剩下的数没办法拿
什么情况下我们可以通过(1)胜利呢?不好分析,所以先分析(2)。
发现当我们交换成 “奇 偶 奇 偶 ... 偶”或者 “偶 奇 偶 奇 偶 ... 奇” 时我们就通过(2)胜利了。
而可以观察到这两种情况n都是偶数,易证当n是奇数时,一定是有数字可以拿的,当n是偶数的时候不一定有数字可以拿(注意是不一定)。
那么当n为奇数时,qcjj拿走一个数。此时n-1是偶数,我们就假设zn有数字可以拿。此时n-2是奇数,qcjj一定有数字可以拿。以此类推。
易证,当n为奇数qcjj始终有数字可以拿,而且qcjj是拿走最后一个数字的人,必赢。
反之亦然,n为偶数zn必赢。
#include <iostream>
using namespace std;//诈骗题
int main()
{ int T;cin>>T;while (T--){int n;int x;cin>>n;for (int i=1;i<=n;++i)cin>>x;if (n&1)cout<<"qcjj"<<'\n';elsecout<<"zn"<<'\n';}return 0;
}智乃的比较函数


这题我本来想放在简单题那里的,因为真的好简单,居然才六百多个人做出来有点惊讶。下面代码可以通过normal version。
思路:直接三重循环枚举a1,a2,a3所有的情况。为什么能枚举呢,因为这三个数具体大小根本不重要,可以任意取,只要能体现他们之间大小关系的所有情况就行了,例如a1>a2>a3,a1=a2>a3等等所有情况。
然后用每种情况去测试n组cmp有没有矛盾,只要有一种情况没有矛盾就是yes。
struct Node {int x, y, z;
}node[N];
int n;
int a[10];
bool check() {rep(i, 1, n) {if (a[node[i].x] < a[node[i].y] && node[i].z == 0) {return false;}if (a[node[i].x] >= a[node[i].y] && node[i].z == 1) {return false;}}return true;
}
void solve() {cin >> n;rep(i, 1, n) {cin >> node[i].x >> node[i].y >> node[i].z;}int f = 0;rep(i, 1, 3) {//a1rep(j, 1, 3) {//a2rep(k, 1, 3) {//a3a[1] = i; a[2] = j; a[3] = k;if (check()) {f = 1;}}}}if (f) cout << "Yes" << endl;else cout << "No" << endl;}难题
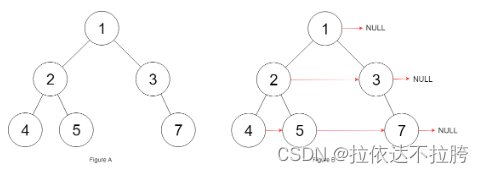
智乃的“黑红树”


个人认为这题比 智乃的36倍数(normal version) 简单,因为这题就是一个模拟建树,自己举出几个样例找找规律还是比较容易的,就是细节会多一点,但下一题考察思维不太容易想到。
分析:
1.是否能建树?
我们可以注意到题中说“如果有子节点,那么一定同时存在两个子节点”,说明要么左孩子右孩子都有,要么没有孩子。根结点是黑色的,因此如果可以建树,黑色结点数一定奇数,红色结点数一定是偶数。但这显然还不够严谨,因为如果有1个黑色结点,100个红色结点,也没法建树。经过简单思考易证b >= r / 2 && b <= 1 + 2 * r才可以建树。如下
if (b % 2 == 1 && r % 2 == 0 && b >= r / 2 && b <= 1 + 2 * r) cout<<"Yes"<<endl;
else cout<<"No"<<endl;2.怎么建树?
按照“完全二叉树”的结构来建树。这样的好处是每个孩子的序号都是从小到大,如果一个根结点有孩子的话,就从小到大输出就行,如果没有就输出-1。
而且孩子的序号也可以确定,因为 lchild = 2*root,rchild = lchild + 1。假如lchild>n或者当前的红/黑结点不够放了,那么root就是没有孩子的。

void solve() {int r, b; cin >> b >> r;int n = r + b;if (b % 2 == 1 && r % 2 == 0 && b >= r / 2 && b <= 1 + 2 * r) {b--;int f = 0;int cur;int level = 1;for (int i = 1; i <= n; i++) {//level为奇数是在为黑层分配红孩子int lc = i * 2, rc = lc + 1;if ((r == 0 || b == 0) && !f) {f = 1;cur = lc;}if (f) {if (cur > n) cout << -1 << " -1" << endl;else if (level % 2 && r == 0) cout << "-1 -1" << endl;//当前在放置红结点,但是红结点没有了else if (level % 2 == 0 && b == 0) cout << "-1 -1" << endl;//跟上面同理else {cout << cur; cur++;cout << " " << cur << endl; cur++;}}else {//红黑结点数都 > 0cout << lc << " " << rc << endl;if (level % 2) r -= 2;else b -= 2;}if (i == pow(2, level) - 1) level++;}}else {cout << "No" << endl;}}另一种更简单的做法,利用队列。
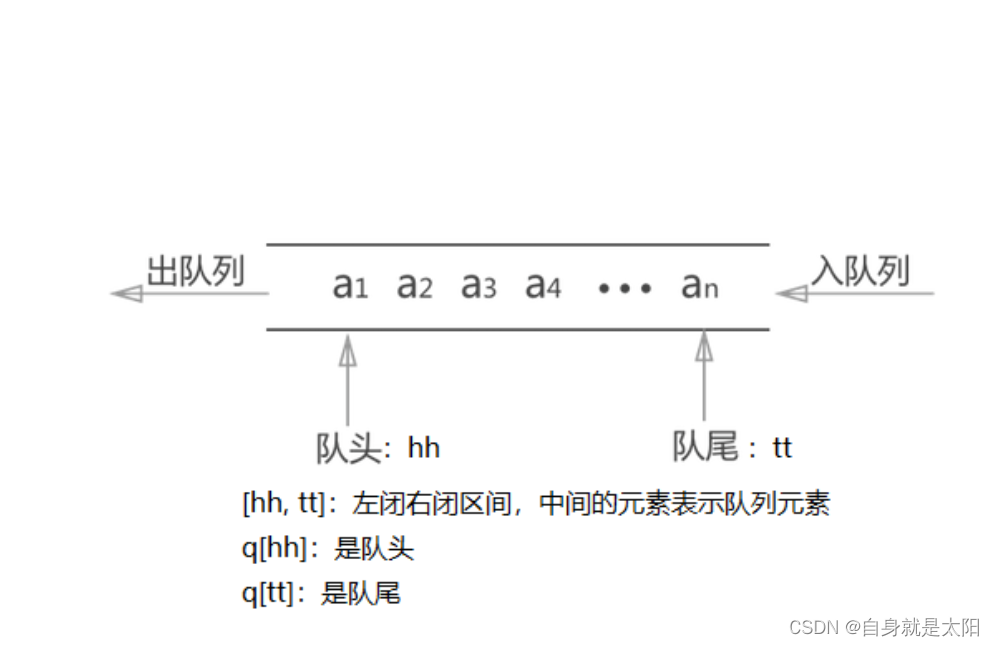
因为我们要按“完全二叉树”的模式建树,也就是从上到下,从左往右建树。这个可以想到遍历二叉树,用的是队列
void solve() {int b, r; cin >> b >> r;queue<int> q;//1代表黑,0代表红q.push(1);if (b % 2 == 1 && r % 2 == 0 && b >= r / 2 && b <= 1 + 2 * r) {cout << "Yes" << endl;b--;int cur = 2;while (!q.empty()) {int t = q.front(); q.pop();if (t == 1) {//要给它红孩子if (r == 0) cout << "-1 -1" << endl;else {cout << cur; cur++;cout << " " << cur << endl; cur++;q.push(0);q.push(0);r -= 2;}}else {if (b == 0) cout << "-1 -1" << endl;else {cout << cur; cur++;cout << " " << cur << endl; cur++;q.push(1);q.push(1);b -= 2;}}}}else cout << "No" << endl;}智乃的36倍数(normal version)

分析:看到题目的时候想,36的倍数都有什么特点,因为之前做过一道题好像也是关于什么的倍数,是有规律可循的,但在这题不行,要另找思路。
这题的正确思路是列出式子,然后变形,涉及到模运算的变换公式-CSDN博客。
对于(ai,aj)组成的数,若是36的倍数,列出
(ai*
+ aj) %36 = 0,k是aj的位数
[(ai*
)%36 + aj%36] % 36 = 0
[ [(ai%36)*(
%36)] % 36 + aj%36 ] %36 = 0
从1-n枚举每一个数当aj,去查询有没有 ai 满足 [(ai%36)*(%36)] % 36 = 36 - aj%36。
事先用哈希表存每个数%36的结果,这样查询的时候就从哈希表的1-35找
总的时间复杂度是O(n)
//0是任何数的倍数
string s[N];
int a[N], b[37];
void solve() {int n; cin >> n;rep(i, 1, n) {cin >> s[i];a[i] = atol(s[i].c_str());b[a[i] % 36]++;}int ans = 0;rep(j, 1, n) {int k = s[j].size();int pj = a[j] % 36;int key = (36 - pj) % 36;int tpm = (int)pow(10, k) % 36;//ten_pow_modfor (int i = 0; i <= 35; i++) {if ((i * tpm) % 36 == key) {ans += b[i];if (pj == i) ans--;}}}cout << ans << endl;
}