话不多说,直接看题:

相当于找一个点使它到3个国家的距离和min,显然,我们不可以枚举点,但是,我们可以对这3个国家分别bfs,然后枚举相加即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
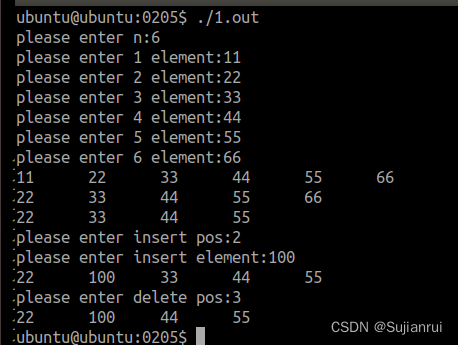
int n,m,v1[1005][1005],v2[1005][1005],v3[1005][1005],mm,mmm,x1,yr,x2,y2,x3,y3,min1=10000000;
char a[1005][1005],q;
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
struct node{int x,y,t;
};
deque<node> qq;
void bfs(int num,int v[][1005],int x,int y){while(!qq.empty()) qq.pop_front();qq.push_back({x,y,0});while(!qq.empty()){node ss=qq.front();qq.pop_front();if(v[ss.x][ss.y]!=-1) continue;v[ss.x][ss.y]=ss.t;for(int i=0;i<4;i++){int xx=ss.x+dir[i][0];int yy=ss.y+dir[i][1];if(xx<=0||xx>n||yy<=0||yy>m) continue;if(a[xx][yy]=='#') continue;if(v[xx][yy]!=-1) continue;if((a[xx][yy]-'0'>=1)&&(a[xx][yy]-'0'<=3)) qq.push_front({xx,yy,ss.t});else qq.push_back({xx,yy,ss.t+1});}}
}
signed main(){memset(v1,-1,sizeof(v1));memset(v2,-1,sizeof(v2));memset(v3,-1,sizeof(v3));cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>q;if(q=='1'){x1=i;yr=j;}if(q=='2'){x2=i;y2=j;}if(q=='3'){x3=i;y3=j;}a[i][j]=q;}}bfs(1,v1,x1,yr);bfs(2,v2,x2,y2);bfs(3,v3,x3,y3);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(v1[i][j]==-1||v2[i][j]==-1||v3[i][j]==-1) continue;if(a[i][j]=='#') continue;if(a[i][j]=='.'&&min1>v1[i][j]+v2[i][j]+v3[i][j]-2)min1=v1[i][j]+v2[i][j]+v3[i][j]-2;if(a[i][j]!='#'&&min1>v1[i][j]+v2[i][j]+v3[i][j])min1=v1[i][j]+v2[i][j]+v3[i][j];}}if(min1==10000000) cout<<-1;else cout<<min1;}有几点主意:
1.合并时分类讨论
2.可能存在2,3已经联通,这样的话算不在123位置上的结果就重复了导致结果偏大。
但是总有一个正确的结果可以获得,与是没有必要判断。
接题:
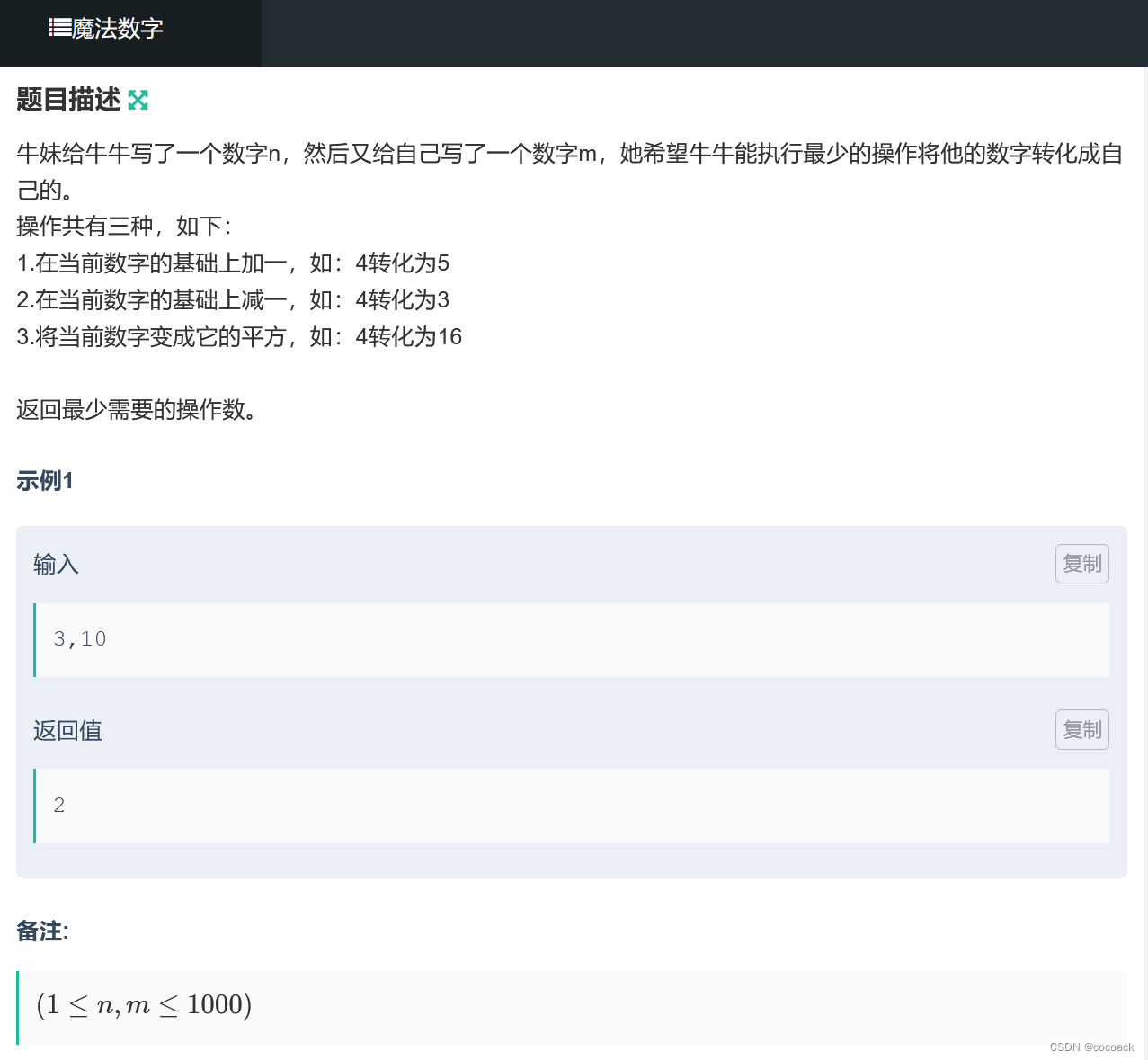
显然,我们最多可以通过abs(n-m)次转化,然后当数大于2*n-m就退出。
其实,负数的存在是没必要的;
于是我们可以BFS,复杂度不超过n-m;
class Solution {
public:int solve(int n, int m) {int vis[3001];struct node{int f,cnt;};queue<node> q;q.push({n,0});vis[n]=1;memset(vis,0,sizeof(vis));while(!q.empty()){node ss=q.front();q.pop();if(ss.f==m){return ss.cnt;}if(ss.cnt>abs(n-m)) continue;int xx=ss.f;for(int i=1;i<=3;i++){xx=ss.f;if(i==1) xx++;else if(i==2) xx--;else xx=xx*xx;if(xx<=0) continue;if(xx>m&&(ss.cnt+xx-m)>=abs(m-n)) continue;if(vis[xx]==1) continue;q.push({xx,ss.cnt+1});vis[xx]=1; }}return -1;}
};接题:
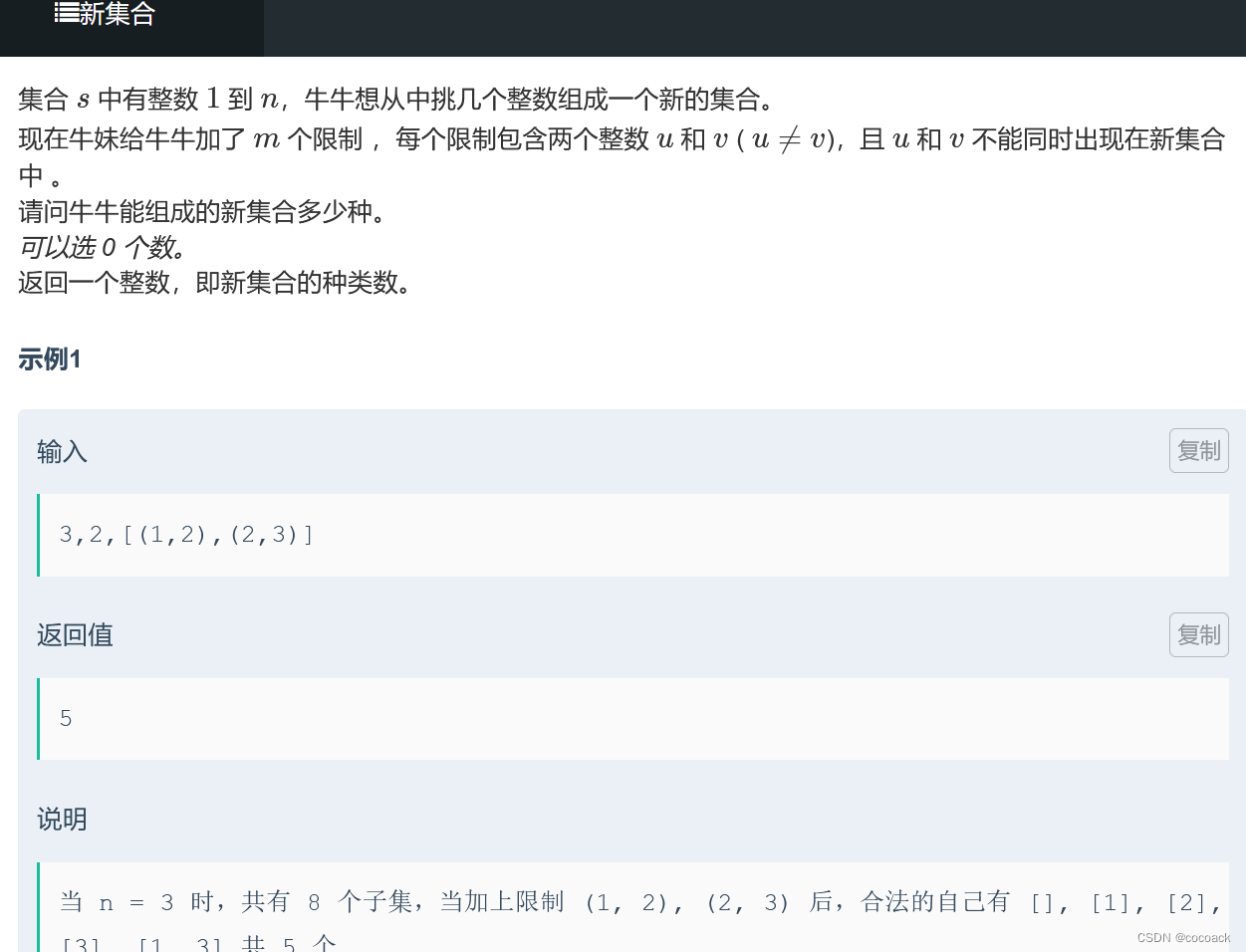
二进制枚举+检验即可,复杂度为(2^n*m)