数据结构：并查集讲解

并查集

- 1.并查集原理
- 2.并查集实现
- 3.并查集应用
- 4.并查集的路径压缩

1.并查集原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。
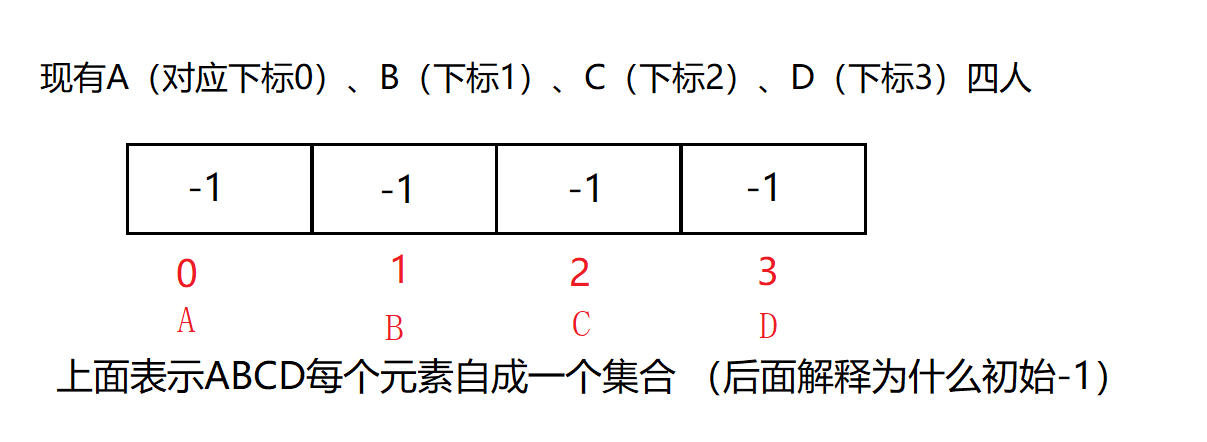
在这里插入图片描述

如何合并两个集合：

先找到两个集合的根部（负数为根部）。
以合并AB为例子，假设让B合并到A，A减去B的值，即变成-2；然后让B的值变成A的下标0。

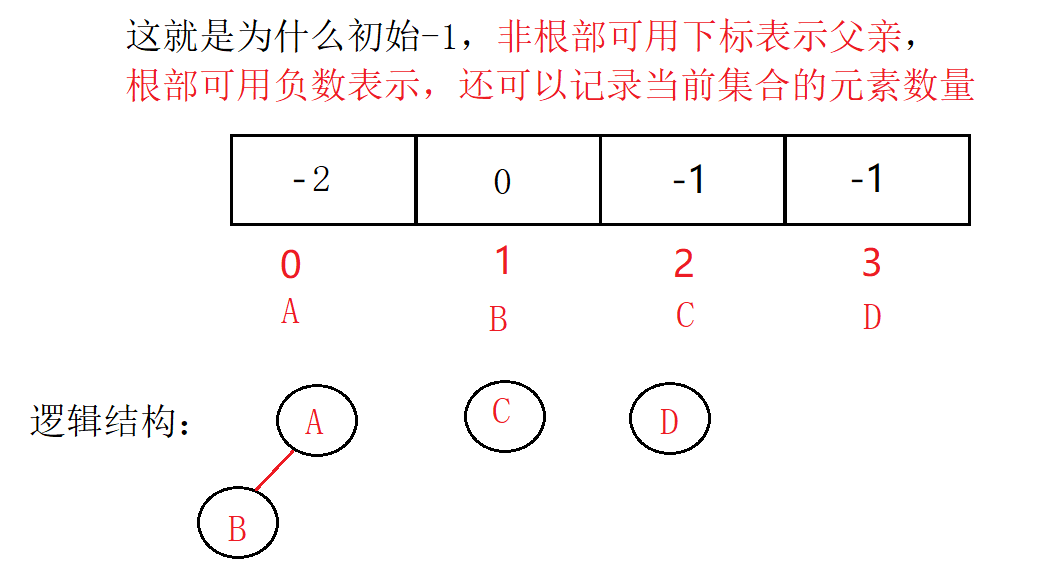
观察合并过程，可以得出以下结论：

数组的下标对应集合中元素的编号
数组中如果为负数，负号代表根，数字代表该集合中元素个数
数组中如果为非负数，代表该元素双亲在数组中的下标

2.并查集实现

并查集一般可以解决以下问题：

查找元素属于哪个集合
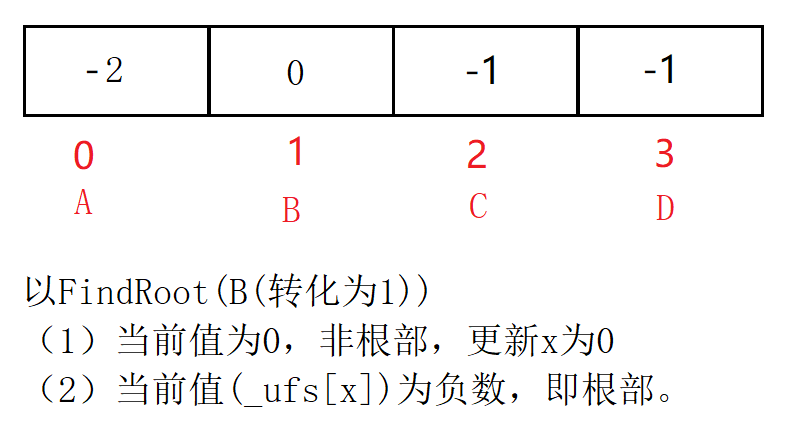
沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)

int FindRoot(int x)  //找根的下标位置
{int par = x;while (_ufs[par] >= 0)  //如果当前大于0，说明未到根部，更新到父亲下标{par = _ufs[par];}return par;
}

在这里插入图片描述

查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在

bool InSet(int x1, int x2)
{if (FindRoot(x1) == FindRoot(x2)){return true;}return false;
}

将两个集合归并成一个集合
前面讲过，不赘述。

void Union(int x1, int x2) //联合这两棵树，默认x2并到x1
{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (abs(_ufs[root1]) < abs(_ufs[root2]))  //让小的一方并到大的一方就这样swap(root1, root2);if (root1 != root2)  //本来不是同一个树（集合）{_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}
}

集合的个数
遍历数组，数组中元素为负数的个数即为集合的个数。

int SetSize()const //返回树的个数
{int size = 0;for (auto e : _ufs)if (e < 0)  size++;return size;
}

完整实现：

class UnionFindSet {
public:UnionFindSet(size_t size)  //一开始全都设置为-1:_ufs(size, -1){}void Union(int x1, int x2) //联合这两棵树，默认x2并到x1{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (abs(_ufs[root1]) < abs(_ufs[root2]))  //让小的一方并到大的一方就这样swap(root1, root2);if (root1 != root2)  //本来不是同一个树（集合）{_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}int FindRoot(int x)  //找根的下标位置{int par = x;while (_ufs[par] >= 0){par = _ufs[par];}return par;}bool InSet(int x1, int x2){if (FindRoot(x1) == FindRoot(x2)){return true;}return false;}int SetSize()const //返回树的个数{int size = 0;for (auto e : _ufs)if (e < 0)  size++;return size;}
private:vector<int> _ufs;
};

3.并查集应用

省份数量

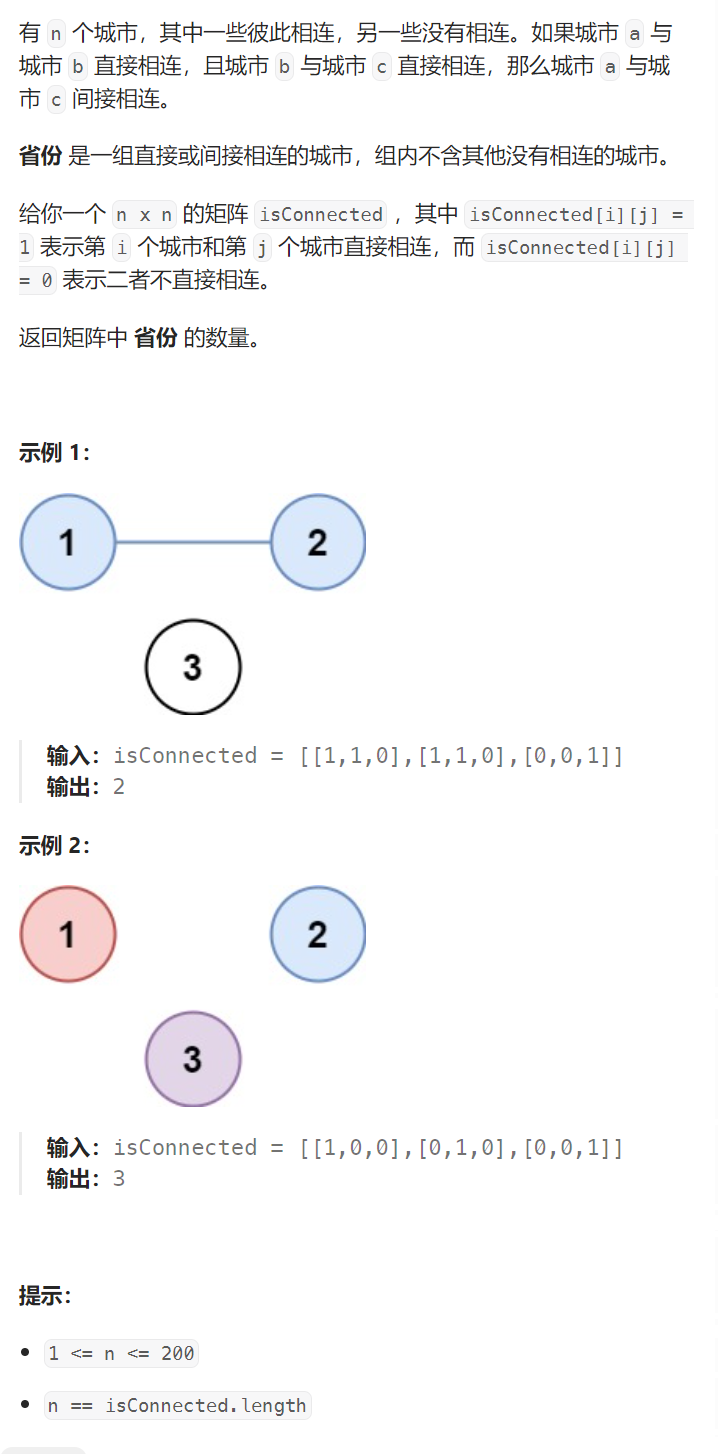
在这里插入图片描述

//讲解：并查集，一个城市就是一个集合
//（1）初始每个城市自成一省
//（2）如果isConnected[i][j]为1，说明i城市和j城市在一个省，合并
//（3）合并完成后遍历数组，负数有几个集合（省份）就有几个
//实际并不一定要实现完整的功能，一般需要的功能是找根部函数class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {vector<int> ufs(isConnected.size(), -1);auto FindRoot = [&ufs](int x){   //找根函数while(ufs[x] >= 0)  //没到根{x = ufs[x];}return x;};for(int i = 0; i < isConnected.size(); i++)for(int j = 0; j < isConnected[i].size(); j++)if(isConnected[i][j] == 1)  //有关系{int root1 = FindRoot(i), root2 = FindRoot(j);if(root1 != root2)  //不是同个集合{ufs[root1] += ufs[root2];  //这一步本题没必要其实ufs[root2] = root1;}}int ret = 0;for(auto e : ufs)  if(e < 0)  ret++;return ret;}
};

等式方程的可满足性

在这里插入图片描述

//思路：并查集，先遍历一次，建立起集合联系，如果a!=b，但a与b在一个集合中，就是相悖的，返回false
// 本题只有小写字母，可用0对应a,1对应b，依次类推
class Solution {
public:bool equationsPossible(const vector<string>& equations) {vector<int> ufs(26, -1);auto FindRoot = [&ufs](int x) {while (ufs[x] >= 0){x = ufs[x];}return x;};//先遍历一次，建立并查集for (auto str : equations)if (str[1] == '='){int root1 = FindRoot(str[0] - 'a'), root2 = FindRoot(str[3] - 'a');if (root1 != root2){ufs[root1] += ufs[root2];  //这一步没必要ufs[root2] = root1;}}//再遍历一次，如果在一个集合中就返回false;for (auto str : equations)if (str[1] == '!'){int root1 = FindRoot(str[0] - 'a'), root2 = FindRoot(str[3] - 'a');if (root1 == root2){return false;}}return true;}
};

4.并查集的路径压缩

并查集一般无需压缩路径，但对数据量大的情况想加快效率就需要压缩路径。

原理：

可在查询时压缩，比如6->5->4->3（根部），先找到根部3。
把6记录下来，一路向上直到根，即让6、5、4直接做3的孩子，从而完成压缩。

int FindRoot(int x)  //找根的下标位置
{int root = x;while (_ufs[root] >= 0){root = _ufs[root];}//压缩路径while (_ufs[x] >= 0){int par = _ufs[x];  //先记录父亲下标_ufs[x] = root;x = par;}return root;
}