原理
当K-means聚类的k值不被指定时,可以通过手肘法来估计聚类数量。
在聚类的过程中,随着聚类数的增大,样本划分会变得更加精细,每个类别的聚合程度更高,那么误差平方和(SSE)会逐渐变小,误差平方和即该类重心与其内部成员位置距离的平方和。SSE是手肘法的核心指标,其公式为: S S E = ∑ i = 1 k ∑ p ∈ C ∣ p − m i ∣ 2 SSE=\sum_{i=1}^{k}\sum_{p\in C}|p-m_i|^2 SSE=i=1∑kp∈C∑∣p−mi∣2 其中, c i c_i ci是第 i 个簇, p p p是 c i c_i ci中的样本点, m i m_i mi是 c i c_i ci的质心( c i c_i ci中所有样本均值),代表了聚类效果的好坏。
当 k 小于真实聚类数时,由于 k 的增大会增加每个簇的聚合程度,故 SSE 的下降幅度会很大;而当 k 到达真实聚类数时,再增加 k 所得到的聚合程度回报会迅速变小,所以 SSE 的下降幅度会骤减,然后随着 k 值的继续增大而趋于平缓。也就是说 SSE 和 k 的关系图是一个手肘的形状,而这个肘部对应的 k 值就是数据的真实聚类数。
代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 显示负号
# 加载数据
X=data.iloc[:, 3:15]
# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 使用PCA进行降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# 使用手肘法确定最佳的K值
inertia = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(X_scaled)inertia.append(kmeans.inertia_)# 绘制手肘法图表
plt.figure(figsize=(8, 4))
plt.plot(range(1, 11), inertia, marker='o', linestyle='--')plt.ylabel('误差平方和')
plt.title('手肘法图表')
plt.savefig('手肘法图.png',dpi=300)
plt.grid(True)plt.show()# 从手肘法图表中选择最佳的K值
# 在这个示例中,根据手肘法,选择K=3# 使用最佳的K值进行K-Means聚类
best_k = 4
kmeans = KMeans(n_clusters=best_k, random_state=42)
kmeans.fit(X_scaled)# 将簇标签添加到原始数据中
data['亚类别'] = kmeans.labels_# 打印每个簇中的样本数量
print(data['亚类别'].value_counts())# PCA绘制降维后的数据及其簇分布
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=kmeans.labels_, cmap='viridis')
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.title('K-Means 结果')
plt.savefig('K-Means 结果.png',dpi=300)
plt.show()
结果:
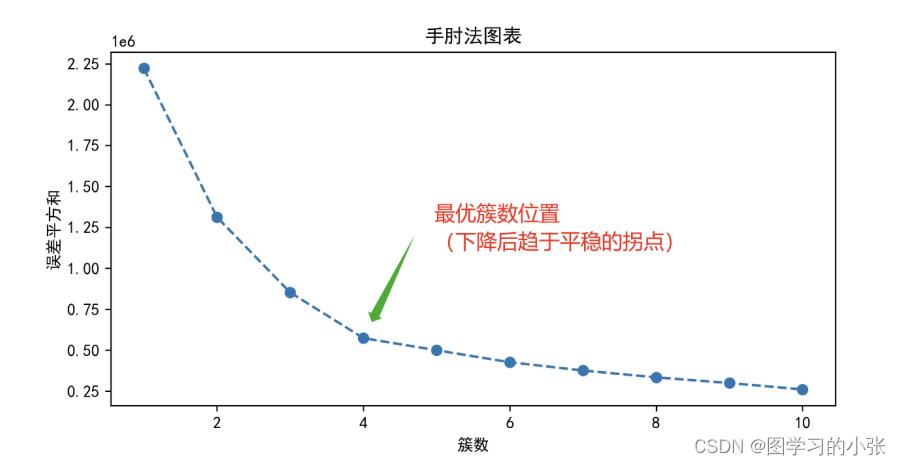
这个问题中,根据手肘法,我们选择最佳k值应该为4。