1. 描述性统计(summary)
对于一个新数据集,首先通过观察来熟悉它,可以打印数据相关信息来大致观察数据的常规特点,比如数据规模(行数列数)、数据类型、类别数量(变量数目、取值范围)、缺失值、异常值等等。然后通过描述性统计来了解数据的统计特性、属性间关联关系、属性与标签的关联关系等。
数据集一般是按照行列组织的,每行代表一个实例,每列代表一个属性。
import pandas as pd
import sys
import numpy as np
import pylab
import matplotlib.pyplot as plt
data = pd.read_csv(r"C:\work\PycharmProjects\machine_learning\filename.csv", index_col=0)
# summary
nrow, ncol = data.shape
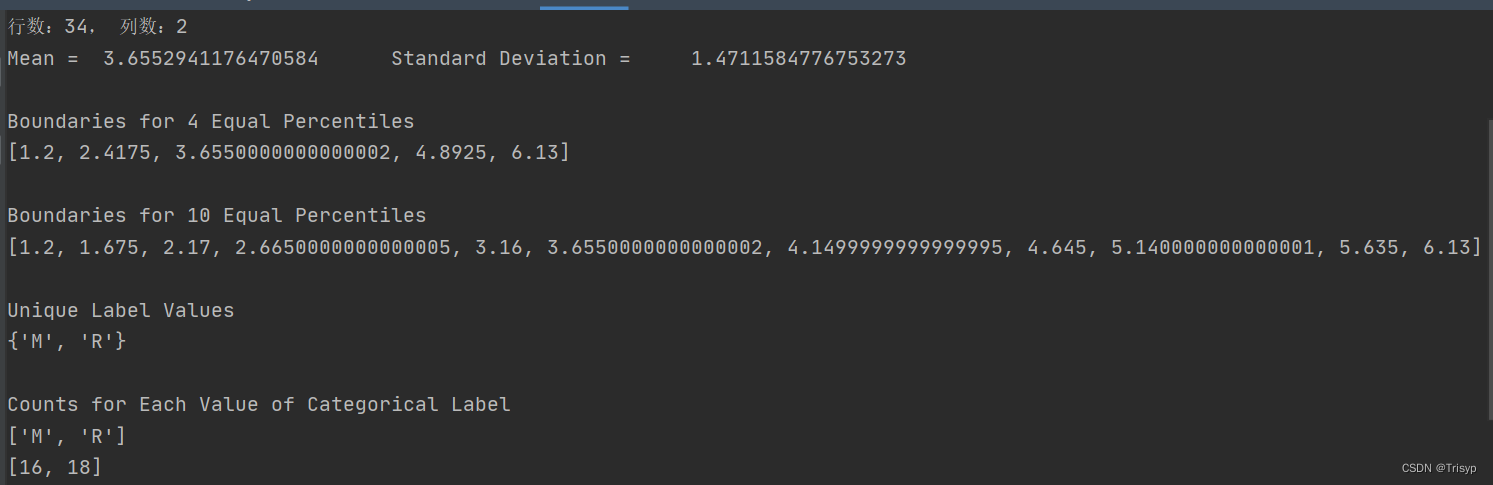
print(f"行数:{nrow}, 列数:{ncol}")
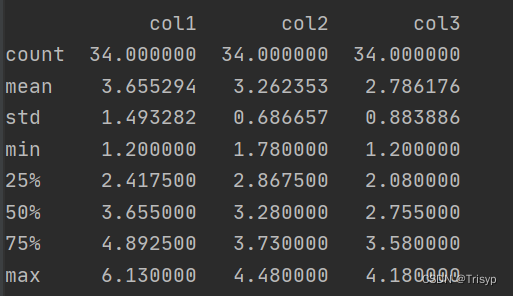
summary = data.describe()
print(summary)
# 箱线图
data_array = data.iloc[:, :3].values
pylab.boxplot(data_array)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges"))
pylab.show()
# 标准化后的箱线图
dataNormalized = data.iloc[:, :3]
for i in range(2):
mean = summary.iloc[1, i]
sd = summary.iloc[2, i]
dataNormalized.iloc[:, i:(i + 1)] = (dataNormalized.iloc[:, i:(i + 1)] - mean) / sd
array3 = dataNormalized.values
pylab.boxplot(array3)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges - Normalized "))
pylab.show()
colArray = np.array(list(data.iloc[:, 0]))
colMean = np.mean(colArray)
colsd = np.std(colArray)
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' +
"Standard Deviation = " + '\t ' + str(colsd) + "\n")
# calculate quantile boundaries(四分位数边界)
ntiles = 4
percentBdry = []
for i in range(ntiles + 1):
percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
# run again with 10 equal intervals(十分位数边界)
ntiles = 10
percentBdry = []
for i in range(ntiles + 1):
percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("Boundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
# The last column contains categorical variables(标签变量)
colData = list(data.iloc[:, 1])
unique = set(colData)
sys.stdout.write("Unique Label Values \n")
print(unique)
# count up the number of elements having each value
catDict = dict(zip(list(unique), range(len(unique))))
catCount = [0] * 2
for elt in colData:
catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))
print(catCount)
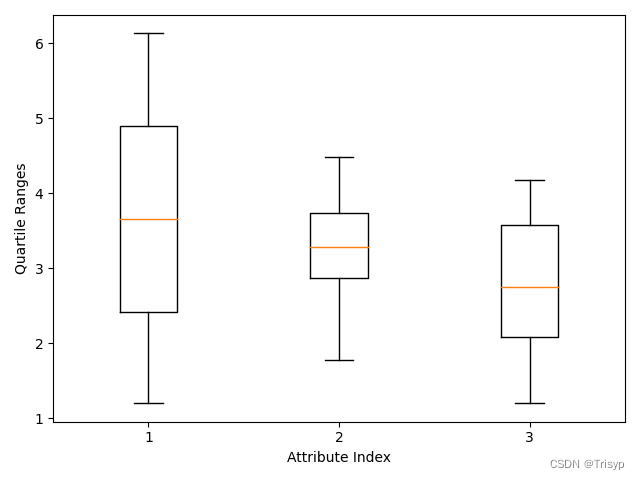
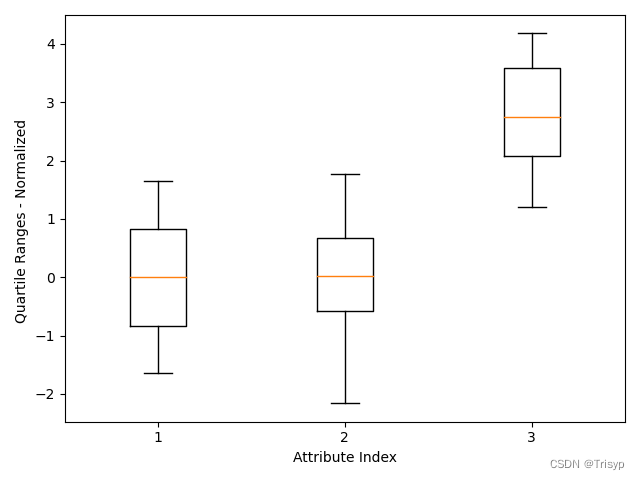
图中显示了一个小长方形,有一个红线穿过它。红线代表此列数据的中位数(第 50 百分位数),长方形的顶和底分别表示第 25 百分位数和第 75 百分位数(或者第一四分位数、第三四分位数)。在盒子的上方和下方有小的水平线,叫作盒须(whisker)。它们分别据盒子的上边和下边是四分位间距的 1.4 倍,四分位间距就是第 75 百分位数和第 25 百分位数之间的距离,也就是从盒子的顶边到盒子底边的距离。也就是说盒子上面的盒须到盒子顶边的距离是盒子高度的 1.4 倍。这个盒须的 1.4 倍距离是可以调整的(详见箱线图的相关文档)。在有些情况下,盒须要比 1.4 倍距离近,这说明数据的值并没有扩散到原定计算出来的盒须的位置。在这种情况下,盒须被放在最极端的点上。在另外一些情况下,数据扩散到远远超出计算出的盒须的位置(1.4 倍盒子高度的距离),这些点被认为是异常点。
2. 二阶统计信息(distribute,corr)
# 分位数图
import scipy.stats as stats
import pylab
stats.probplot(colArray, dist="norm", plot=pylab)
pylab.show()

如果此数据服从高斯分布,则画出来的点应该是接近一条直线。
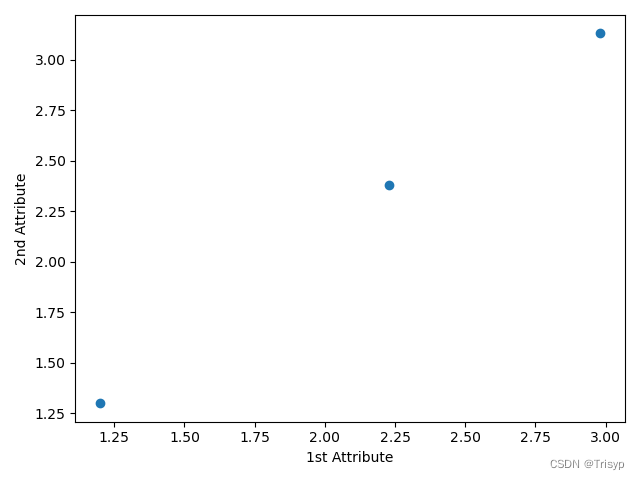
# 属性间关系散点图
import matplotlib.pyplot as plt
data_row1 = data.iloc[0, :3]
data_row2 = data.iloc[1, :3]
plt.scatter(data_row1, data_row2)
plt.xlabel("1st Attribute")
plt.ylabel(("2nd Attribute"))
plt.show()
# 属性和标签相关性散点图
from random import uniform
target = []
for i in range(len(colData)):
if colData[i] == 'R': # R用1代表, M用0代表
target.append(1)
else:
target.append(0)
plt.scatter(data_row1, target)
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()
target = []
for i in range(len(colData)):
if colData[i] == 'R': # R用1代表, M用0代表
target.append(1+uniform(-0.1, 0.1))
else:
target.append(0+uniform(-0.1, 0.1))
plt.scatter(data_row1, target, alpha=0.5, s=120) # 透明度50%
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()

第二个图绘制时取 alpha=0.5,这样这些点就是半透明的。那么在散点图中若多个点落在一个位置就会形成一个更黑的区域。

# 关系矩阵及其热图
corMat = pd.DataFrame(data.corr())
plt.pcolor(corMat)
plt.show()

属性之间如果完全相关(相关系数 =1)意味着数据可能有错误,如同样的数据录入两次。多个属性间的相关性很高(相关系数 >0.7),即多重共线性(multicollinearity),往往会导致预测结果不稳定。属性与标签的相关性则不同,如果属性和标签相关,则通常意味着两者之间具有可预测的关系
# 平行坐标图
minRings = summary.iloc[3, 2] # summary第3行为min
maxRings = summary.iloc[7, 2] # summary第7行为max
for i in range(nrow):
# plot rows of data as if they were series data
dataRow = data.iloc[i, :3]
labelColor = (data.iloc[i, 2] - minRings) / (maxRings - minRings)
dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()
# 对数变换后平行坐标图
meanRings = summary.iloc[1, 2]
sdRings = summary.iloc[2, 2]
for i in range(nrow):
dataRow = data.iloc[i, :3]
normTarget = (data.iloc[i, 2] - meanRings) / sdRings
labelColor = 1.0 / (1.0 + np.exp(-normTarget))
dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()
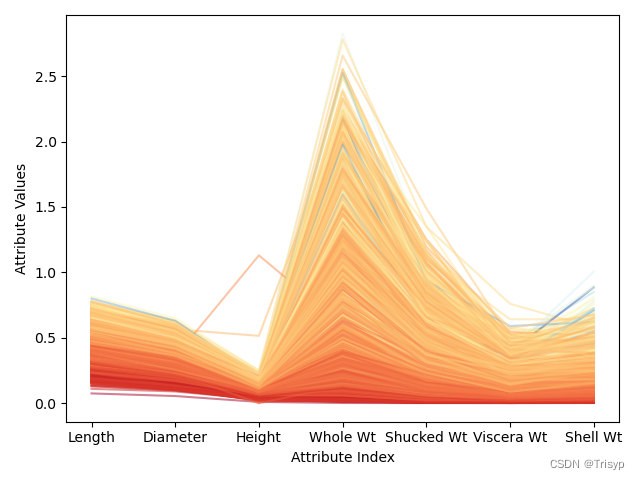
在属性值相近的地方,折线的颜色也比较接近,则会集中在一起。这些相关性都暗示可以构建相当准确的预测模型。相反,有些微弱的蓝色折线与深橘色的区域混合在一起,说明有些实例可能很难正确预测。
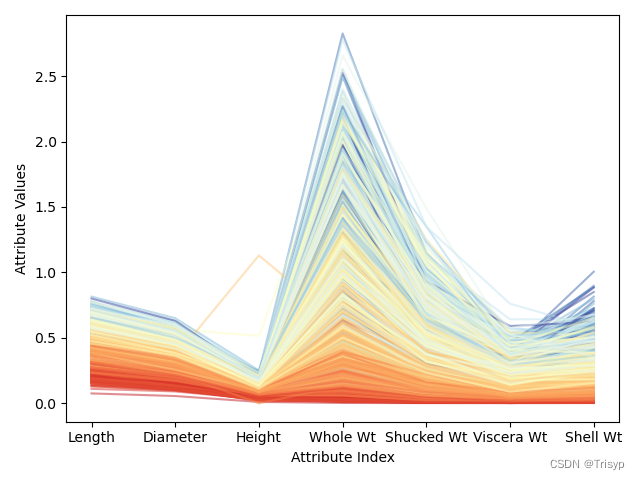
转换后可以更充分地利用颜色标尺中的各种颜色。注意到针对某些个属性,有些深蓝的线(对应年龄大的品种)混入了浅蓝线的区域,甚至是黄色、亮红的区域。这意味着,当该属性值较大时,仅仅这些属性不足以准确地预测出鲍鱼的年龄。好在其他属性可以很好地把深蓝线区分出来。这些观察都有助于分析预测错误的原因。
3. 完整代码(code)
import pandas as pd
import sys
import numpy as np
import pylab
import matplotlib.pyplot as pltdata = pd.read_csv(r"C:\work\PycharmProjects\machine_learning\filename.csv", index_col=0)nrow, ncol = data.shape
print(f"行数:{nrow}, 列数:{ncol}")
summary = data.describe()
print(summary)data_array = data.iloc[:, :3].values
pylab.boxplot(data_array)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges"))
pylab.show()dataNormalized = data.iloc[:, :3]
for i in range(2):mean = summary.iloc[1, i]sd = summary.iloc[2, i]dataNormalized.iloc[:, i:(i + 1)] = (dataNormalized.iloc[:, i:(i + 1)] - mean) / sdarray3 = dataNormalized.values
pylab.boxplot(array3)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges - Normalized "))
pylab.show()colArray = np.array(list(data.iloc[:, 0]))
colMean = np.mean(colArray)
colsd = np.std(colArray)
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' +"Standard Deviation = " + '\t ' + str(colsd) + "\n")# calculate quantile boundaries(四分位数边界)
ntiles = 4
percentBdry = []
for i in range(ntiles + 1):percentBdry.append(np.percentile(colArray, i * (100) / ntiles))sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")# run again with 10 equal intervals(十分位数边界)
ntiles = 10
percentBdry = []
for i in range(ntiles + 1):percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("Boundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")# The last column contains categorical variables(标签变量)
colData = list(data.iloc[:, 3])
unique = set(colData)
sys.stdout.write("Unique Label Values \n")
print(unique)# count up the number of elements having each value
catDict = dict(zip(list(unique), range(len(unique))))
catCount = [0] * 2
for elt in colData:catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))
print(catCount)# 分位数图
import scipy.stats as statsstats.probplot(colArray, dist="norm", plot=pylab)
pylab.show()# 属性间关系散点图
data_row1 = data.iloc[:, 0]
data_row2 = data.iloc[:, 1]
plt.scatter(data_row1, data_row2)
plt.xlabel("1st Attribute")
plt.ylabel(("2nd Attribute"))
plt.show()# 属性和标签相关性散点图
from random import uniformtarget = []
for i in range(len(colData)):if colData[i] == 'R': # R用1代表, M用0代表target.append(1)else:target.append(0)
plt.scatter(data_row1, target)
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()target = []
for i in range(len(colData)):if colData[i] == 'R': # R用1代表, M用0代表target.append(1 + uniform(-0.1, 0.1))else:target.append(0 + uniform(-0.1, 0.1))
plt.scatter(data_row1, target, alpha=0.5, s=120) # 透明度50%
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()# 关系矩阵及其热图
corMat = pd.DataFrame(data.corr())
plt.pcolor(corMat)
plt.show()# 平行坐标图
minRings = summary.iloc[3, 2] # summary第3行为min
maxRings = summary.iloc[7, 2] # summary第7行为max
for i in range(nrow):# plot rows of data as if they were series datadataRow = data.iloc[i, :3]labelColor = (data.iloc[i, 2] - minRings) / (maxRings - minRings)dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()meanRings = summary.iloc[1, 2]
sdRings = summary.iloc[2, 2]
for i in range(nrow):dataRow = data.iloc[i, :3]normTarget = (data.iloc[i, 2] - meanRings) / sdRingslabelColor = 1.0 / (1.0 + np.exp(-normTarget))dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()