回归与分类

1 Logistic 回归

1. 定义

   目标：给定数据点 $X^{(n)}\in R^m$ 和相应标签 $t^{(n)}\in \Omega$ ，找到一个映射 $f:R^m\to \Omega$

   • 回归的目的是预测一个连续的数值变量，如果Ω是一个连续的集合称其为回归(regression)
   • 分类的目的是将数据划分为离散的类，如果Ω是一个离散的集合称其为分类(classification)

2. 回归类型

   • 线性回归：用于建立因变量和自变量之间线性关系的统计方法
     $$f(x)=wx+\beta$$
     其中，$y$是因变量，$x_1,x_2,\cdots ,x_n$是自变量，${\beta }_0,{\beta }_1,\cdots ,{\beta }_n$是回归系数。

   • 多项式回归：多项式回归是一种扩展了线性回归的方法，它可以拟合因变量和自变量之间的非线性关系。
     $$f(x)=\beta +w_{1}x+w_2{x}^2+w_3{x}^3+\cdots +w_m{x}^m$$
     其中，$m$是多项式的最高次数。

   通过均方误差 （$MSE=\frac{1}{n}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$）进行训练，得到最终的 $f(x)$。

3. 分类方法

   • 线性回归分类：感知机、SVM

   • 非线性回归分类：sigmoid function
     $$f(x)=\frac{1}{1+e^{-x}}$$
     

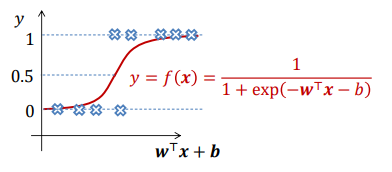
   • 伯努利分布假设
     $$P(x)=\{\begin{array}{l}p,x=1\\ 1-p,x=0\end{array}$$

4. Logistic 回归

   Logistic 回归是一种用于二分类问题的模型，它可以预测一个离散输出，例如0或1。

   • Logistic回归函数

     对于二分类问题，一个0-1单元足以表示一个标签
     $$P(t=1|x)=\frac{1}{1+e^{-{\theta }^{\top }x}}\triangleq h(x)$$
     其中$x$是输入，$t$ 是标签，$\theta$ 是参数。我们的目标是寻找一个$\theta$值使得概率$P(t=1|x)=h(x)$​。

     我们实质上是在用另一个连续函数来“回归”一个离散的函数(x→t）

   • 最大化条件数据似然

     最大化条件数据似然是一种参数估计方法，它利用已知的数据和条件分布，找到最有可能（即最大概率）导致这种分布的参数值。

     将t看作一个伯努利变量，并且$P(t=1|x)=h(x;\theta )$​。条件似然函数为
     $$P(t^{(1)},...,t^{(n)}|X;\theta )=\prod _{n=1}^{N}h(x^{(n)}{)}^{t^{(n)}}(1-h(x^{(n)}{)}^{1-t^{(n)}}$$
     最大化似然等同于最小化下式：
     $$E(\theta )=-\frac{1}{n}lnP(t^{(1)},...,t^{(n)})=-\frac{1}{n}\sum _{n=1}^n\left(t^{(n)}lnh(x^{(n)}+(1-t^{(n)})ln(1-h(x^{(n)})\right)$$

   • 交叉熵误差函数

     对于带有二元标签的一组训练样本$\{(x^{(n)},t^{(n)}):n=1,...,N\}$，定义交叉熵误差（cross-entropyerror）函数
     $$E(\theta )=-\frac{1}{n}lnP(t^{(1)},...,t^{(n)})=-\frac{1}{n}\sum _{n=1}^n\left(t^{(n)}lnh(x^{(n)}+(1-t^{(n)})ln(1-h(x^{(n)})\right)$$

5. 训练和测试

   • 计算梯度
     $$\nabla E(\theta )=\frac{1}{N}\sum _N{x}^{(n)}(h(x^{(n)})-t^{(n)})$$

   • 一些正则化项添加到成本函数中
     $$J(\theta )=E(\theta )+\lambda |\theta {|}^2/2$$

   • 训练：学习θ来最小化成本函数，其中$\alpha$是学习率。
     $$\theta \leftarrow \theta -\alpha \nabla J(\theta )$$

   • 测试：对于新的输入$x$，如果$P(t=1|x)>P(t=0|x)$，则可以预测输入为类别1，否则就是类别0。

2 Softmax 回归

1. 类别标签的表示

   one-hot编码(1-of-K)：将离散的类别标签转换为向量形式，其中每个类别都由一个唯一的二进制值表示。

   对于一个具有 $K$ 个可能类别的问题，1-of-K 表示法将每个类别映射为一个长度为 $K$ 的二进制向量，其中只有一个元素为1，其余为0。被设置为1的位置对应于类别的索引。

   例如，对于一个三类分类问题（$K=3$），类别A、B和C可能被表示为：

   • 类别A：$1,0,0$
   • 类别B：$0,1,0$
   • 类别C：$0,0,1$

   • 唯一性： 每个类别的表示是唯一的，因为只有一个元素为1。
   • 独立性： 每个类别的表示与其他类别的表示是相互独立的，不存在冗余信息。

2. 分布假设

   • 正态分布假设

     正态分布假设是指假设数据集服从正态分布的概率分布。
     $$f(x;\mu ,\sigma )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$
     其中，$\mu$ 是均值（分布的中心），$\sigma$ 是标准差（度量分布的离散程度）。

   • Multinoulli分布假设

     Multinoulli分布假设描述了离散型随机变量的概率分布，特别适用于多类别分类问题。

     对于一个给定的样本，其类别的概率分布可以由参数 ${\varphi }_k$ 来表示。对于一个离散型随机变量 $X$ 表示类别的取值，其概率质量函数如下：
     $$P(X=k)={\varphi }_k$$
     这表示样本属于类别 $k$ 的概率为 ${\varphi }_k$ 。

3. Softmax 函数

   Softmax回归，也称为多类逻辑回归或多类交叉熵分类，是一种用于多类别分类的模型。

   假设有 $K$ 个类别，对于输入特征向量$x$​ ，Softmax回归的模型表达式如下：
   $$P(y=k\mid x)=\frac{e^{w_k\cdot x+b_k}}{{\sum }_{j=1}^K{e}^{w_j\cdot x+b_j}}$$
   其中，$P(y=k\mid x)$ 是给定输入 $x$ 属于类别 $k$ 的概率。$ w_k $ 和 $ b_k $ 是模型的参数，分别表示第 $k$个类别的权重和偏置。

4. 最大条件似然

   最大条件似然的目标是找到一组参数，使得在给定输入 $x$ 的条件下，观察到实际类别 $y$ 的概率最大。Softmax 回归的最大条件似然目标函数为：
   $$P(t^{(1)},...,t^{(N)}|X)=\prod _{n=1}^N\prod _{k=1}^{K}P(t_k^{(n)}=1|x^{(n)}{)}^{t_k^{(n)}}$$
   其中：

   • $N$ 是样本数量。
   • $t_k^{(n)}$ 是one-hot函数，当 $t_k$ 等于 $k$ 时为1，否则为0。

5. 交叉摘误差函数

   Softmax回归通常使用交叉熵损失函数来衡量模型预测与实际类别之间的差异。对于 $N$​ 个样本，交叉熵损失函数的表达式为：
   $$J(w,b)=-\frac{1}{N}\sum _{i=1}^N\sum _{k=1}^K{t}_k^{(n)}\ln P(t_k^{(n)}=1|x^{(n)})$$
   其中：

   • $J(w, b) $ 是损失函数。