线性回归

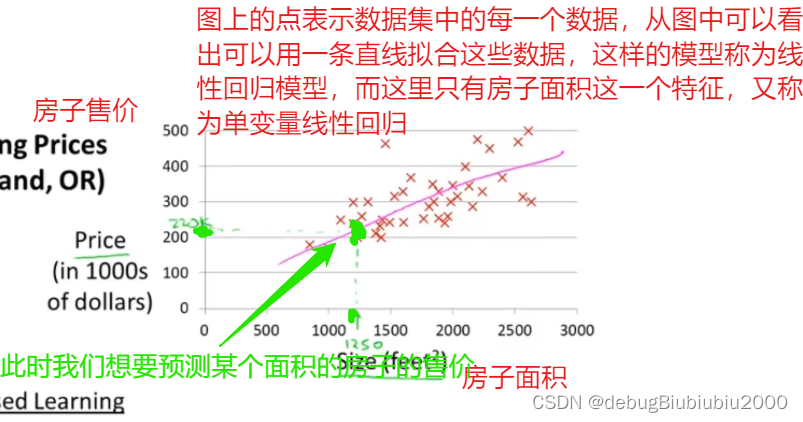
还是以之前的预测房价为例，根据不同尺寸的房子对应不同的售价组成的数据集画图，图如下

监督学习算法工作流程

假设函数其实就是我们所说的函数，在房价这个例子中，我们可以从上图中看出房价和房子面积是一个一元的线性函数（当然有更复杂更贴近数据集的函数拟合数据集，但是我们从最简单的开始学习），所以我们要来预测y关于x的线性函数，可以简单写成：y = h(x)，但它更完整的写法是下图的形式：

接下来的例子中会用到的一些符号

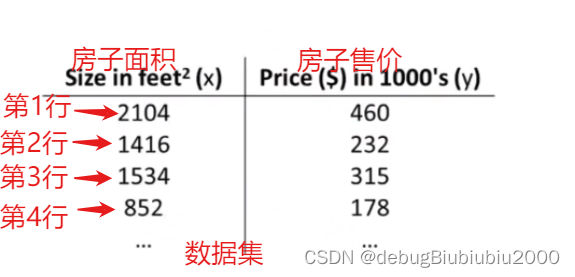
训练集：数据集又称为训练集，如下面的房价数据集

小写字母m：训练集中样本的数量，也就是数据集中总的数据个数

小写字母x：输入变量，这里指的是房子的面积

小写字母y：输出变量，预测的对应面积x的房子售价

(x, y)：表示某一个训练样本，如房价数据集中的某一行数据

(x^i, y^i)；i是上标，表示第i个样本

代价函数

下面介绍的代价函数称为平方误差函数，有时还称为平方误差代价函数。，是代价函数中的一种，在解决线性回归问题中比较常用，当然还有其他代价函数

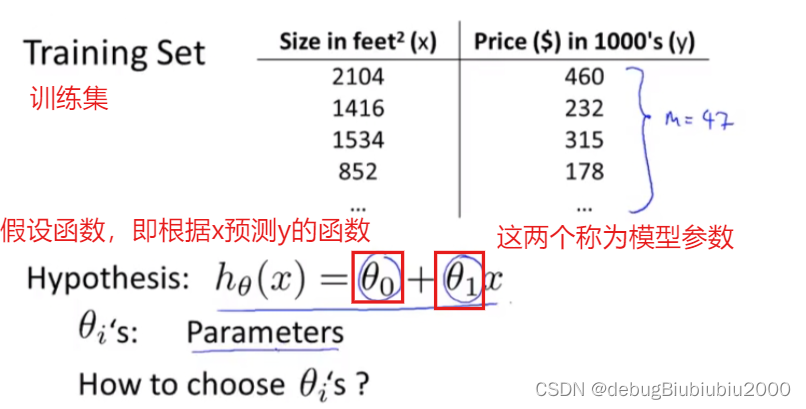
模型参数介绍

如图，我们要做的是如何选择两个模型参数，以让假设函数更贴近训练集，也就是选择对两个模型参数θ0和θ1，会让预测结果更准确

 模型参数的选择

选择不同的模型参数，会得到不同的假设函数

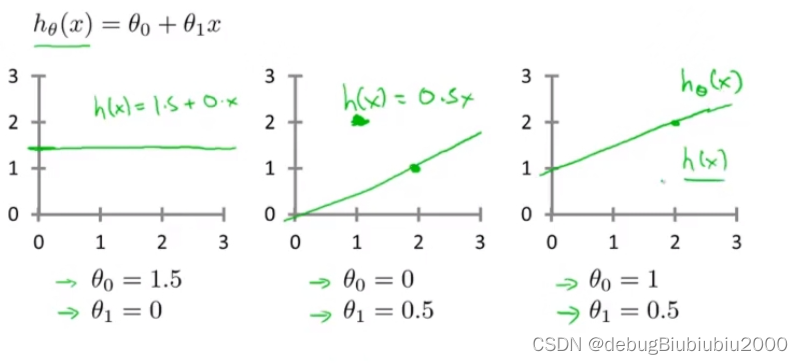
现在我们要根据训练集，得出两个模型参数的值，进而得到具体的假设函数，让该假设函数尽可能多的与训练集中的数据点拟合。那我们该怎么选择这两个模型参数呢？

思路是：对于训练集中的每个数据，每个房子面积x都对应着已知的售价y，假如已经确定两个模型参数，即已经得到假设函数，应该使得对该假设函数输入训练集中的某个x得到的yy，与实际的y最接近（也就是我们说的要最大程度的拟合数据点）

总之就是，我们要使得预测的房价和真实的售价之间差值的平方越小越好（至于为什么是平方，是因为预测价和真实价的差值可能正可能负）

代价函数的数学定义

理解代价函数

为了更好理解，现在我们简化一下假设函数，如图（因为公式不好写，所以都用截图表示了）

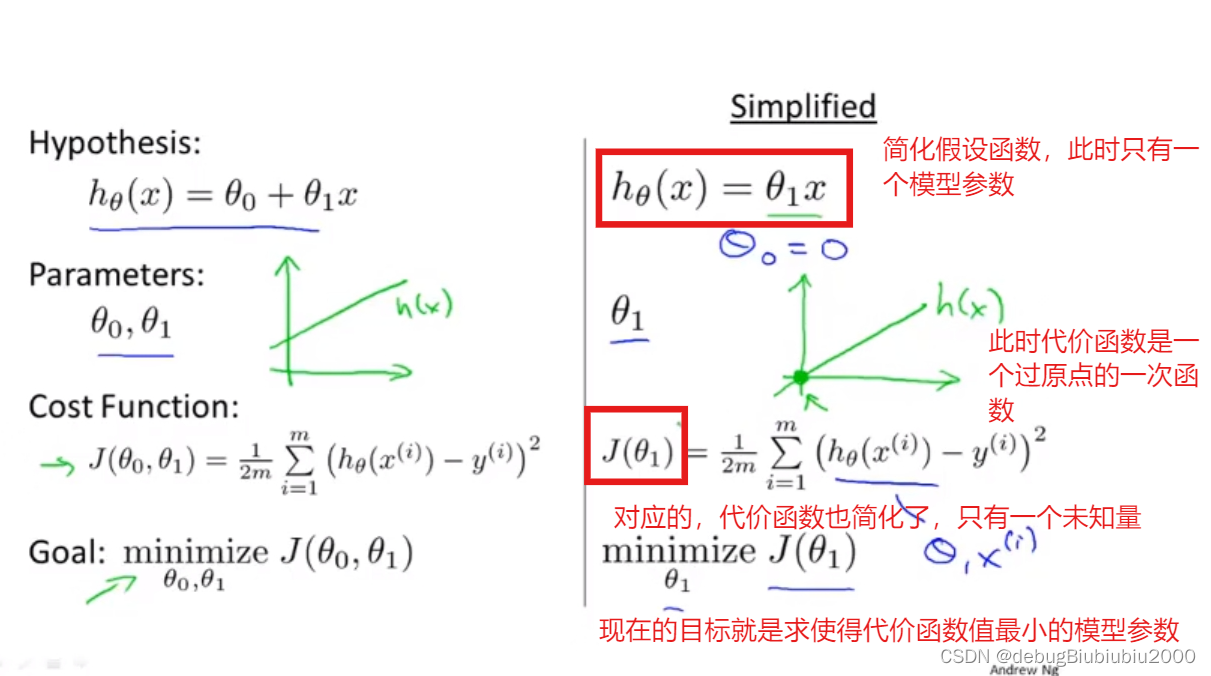
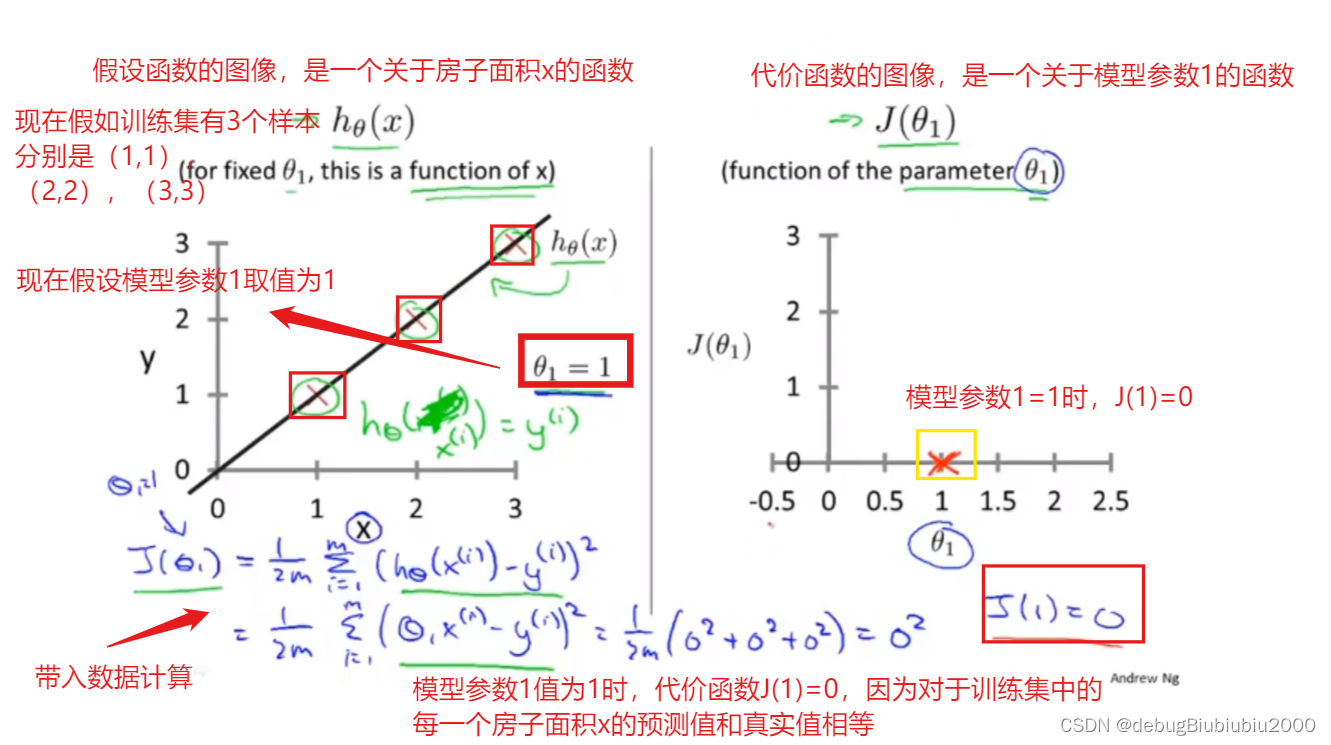
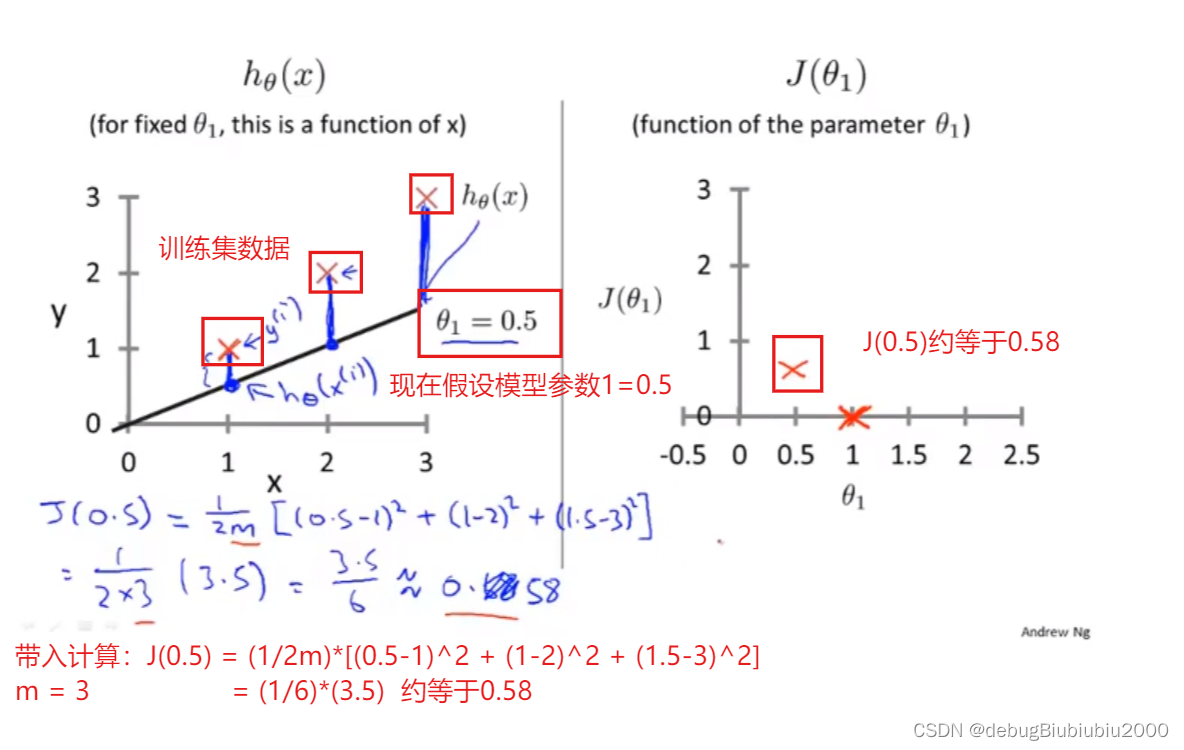
 θ1可以取不同的值，包括正数、负数、0，我们的目标是找到让J(θ1)最小的θ1，由J(θ1)的图像可以看出，在这个例子中，θ1 = 1时，J(θ1)能取到最小值，而当θ1=1时，假设函数也是能最大程度的拟合训练集的每个样本的（在这个例子中，假设函数完全拟合训练集中的三个数据点）

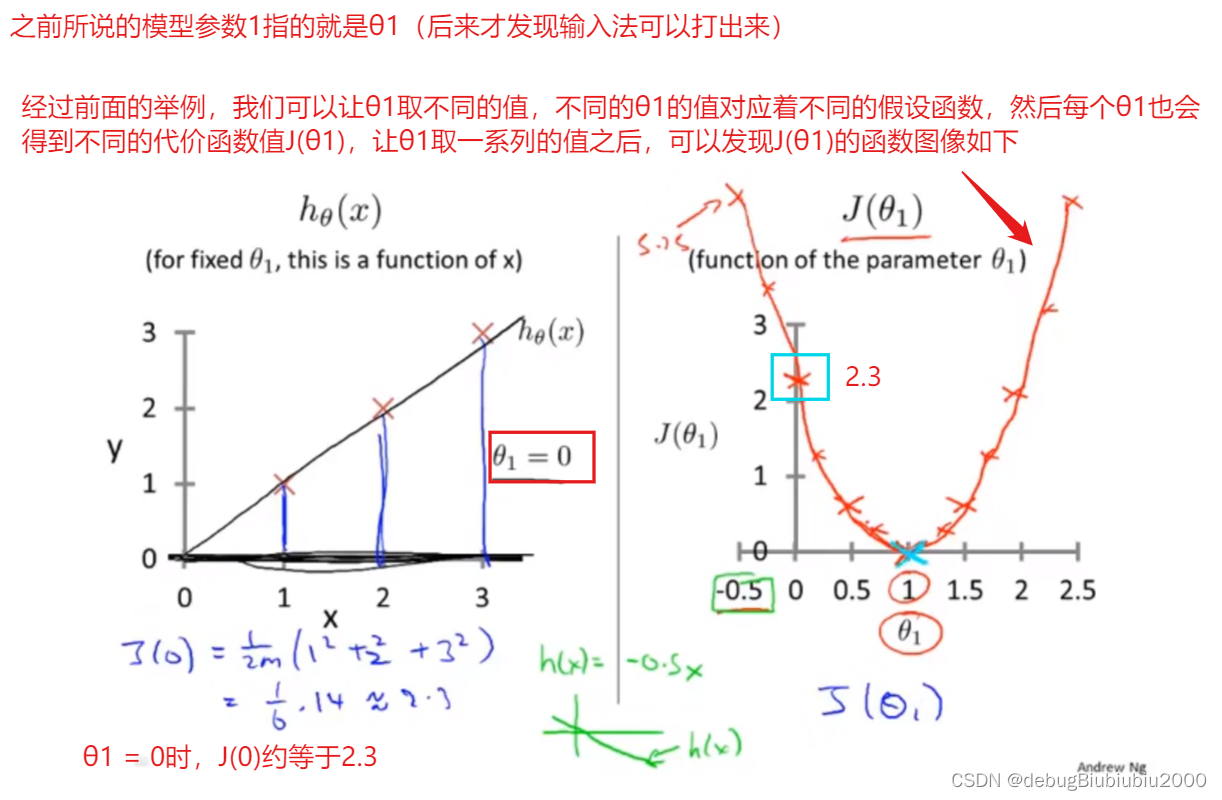
上面我们为了容易理解，简化了假设函数，让θ0=0，即假设函数中只有一个模型参数，现在讨论原本的假设函数（有两个模型参数θ0，θ1）

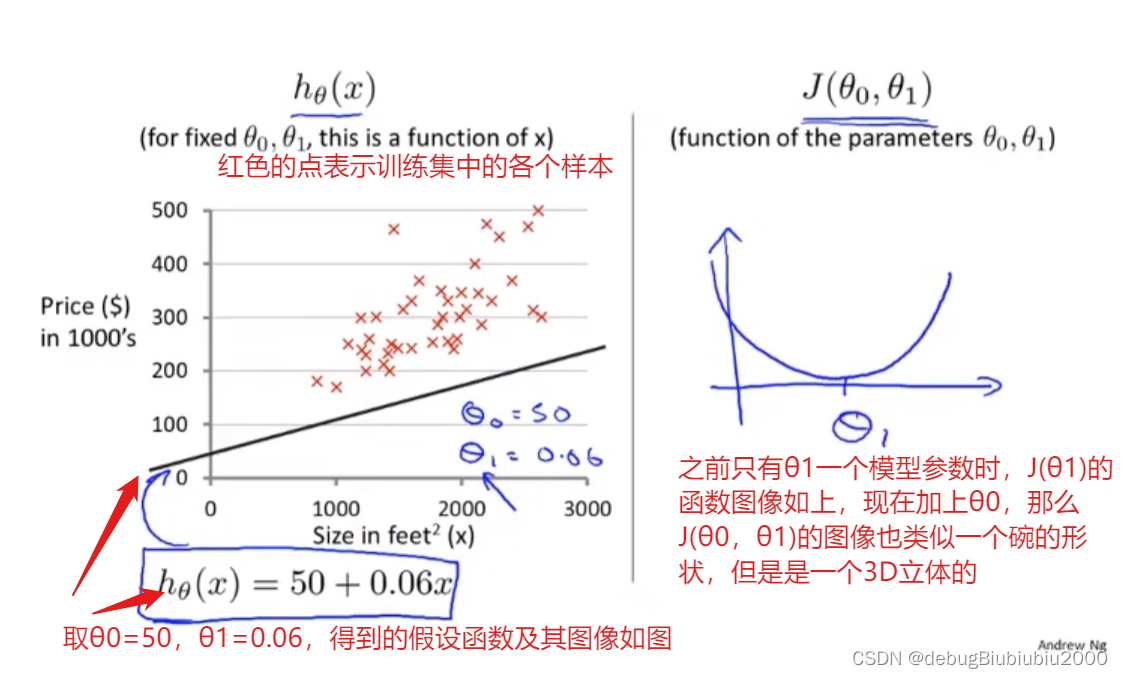
代价函数J(θ0，θ1)的函数图像如下：

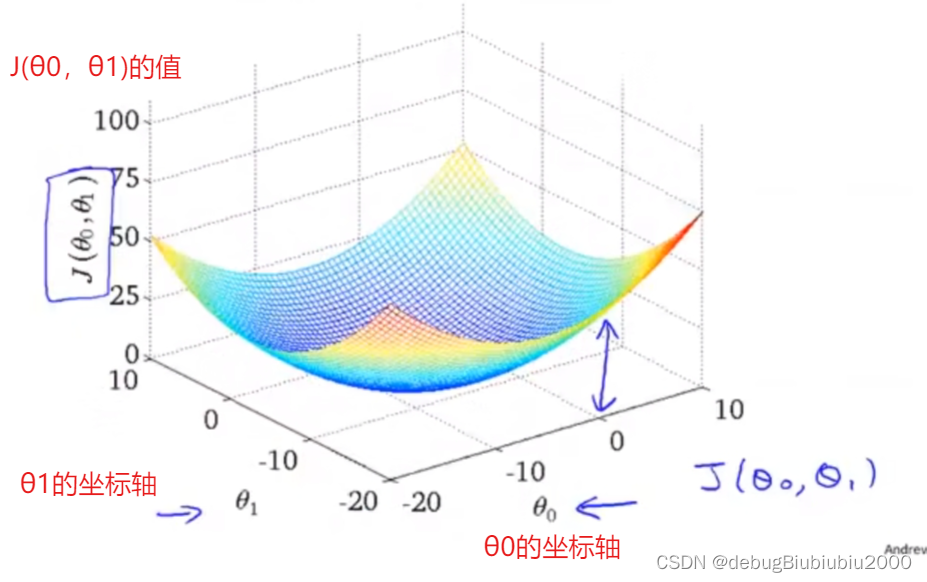
 我们用等高线图代替上面的立体图，可以看出，越接近等高线图的中心，代价函数的值就越小，而对应的假设函数就越拟合训练集数据。

我们都是随便取某个点来进行分析，但是实际上不可能一个个列举，所以算法要做的就是快速找到最小的代价函数值J(θ0，θ1)对应的θ0和θ1.

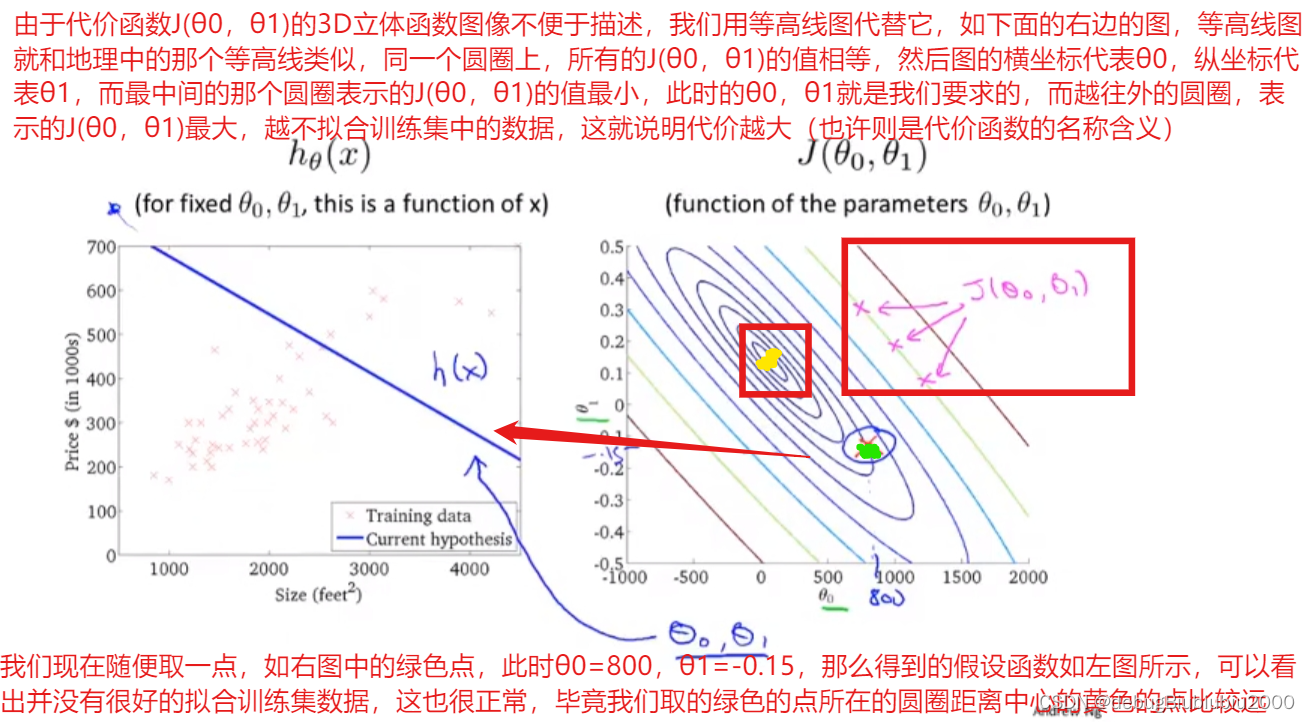
梯度下降算法

上面我们的需求是想得到最小的代价函数值，那么我们此时可以使用梯度下降算法来实现这个需求。梯度下降算法不仅仅可以最小化线性回归的代价函数，还可以最小化其他函数，即梯度下降算法可以最小化任意函数，被广泛应用于机器学习的众多领域。

梯度下降算法可以最小化任意函数J(θ0，θ1，θ2，...，θn)，即得到任意函数的最小值或局部最小值，下面为了更容易理解，以两个模型参数为例J(θ0，θ1)描述梯度下降算法的思路

在每一个位置选择不同方向的路时，实际上上就是在不断修改θ0和θ1的值

梯度下降算法的数学定义

公式中的α控制着以多大幅度更新参数θj

梯度下降算法的理解

导数项的意义

我们先来看导数的概念及基本含义，这里只写出了最基本的一点（来自百度，因为我也忘完了(╥╯^╰╥)）：

导数是用来描述函数局部变化率的度量。对于给定的函数，它在某一点处的导数，就是函数曲线在该点处的切线斜率。具体地说，若函数y=f(x)在点x0处可导，则点(x0, f(x0))处切线的斜率就是f(x)在点x0处的导数f'(x0)。导数本质上是一个极限，即函数在某个点x0处的导数，就是其在此点附近取极限时的极限值，即：f'(x0) = lim (x->x0) [f(x) - f(x0)] / [x - x0]

为了容易理解，现在假设代价函数只有一个模型参数，即J(θ1)，跟之前一样，我们可以得到J(θ1)的函数图像如下，由上面的导数概念，可以知道函数J(θ1)在位置A的导数，就是在函数图像上的位置A作一条切线，该切线的斜率就是J(θ1)在位置A的导数值。

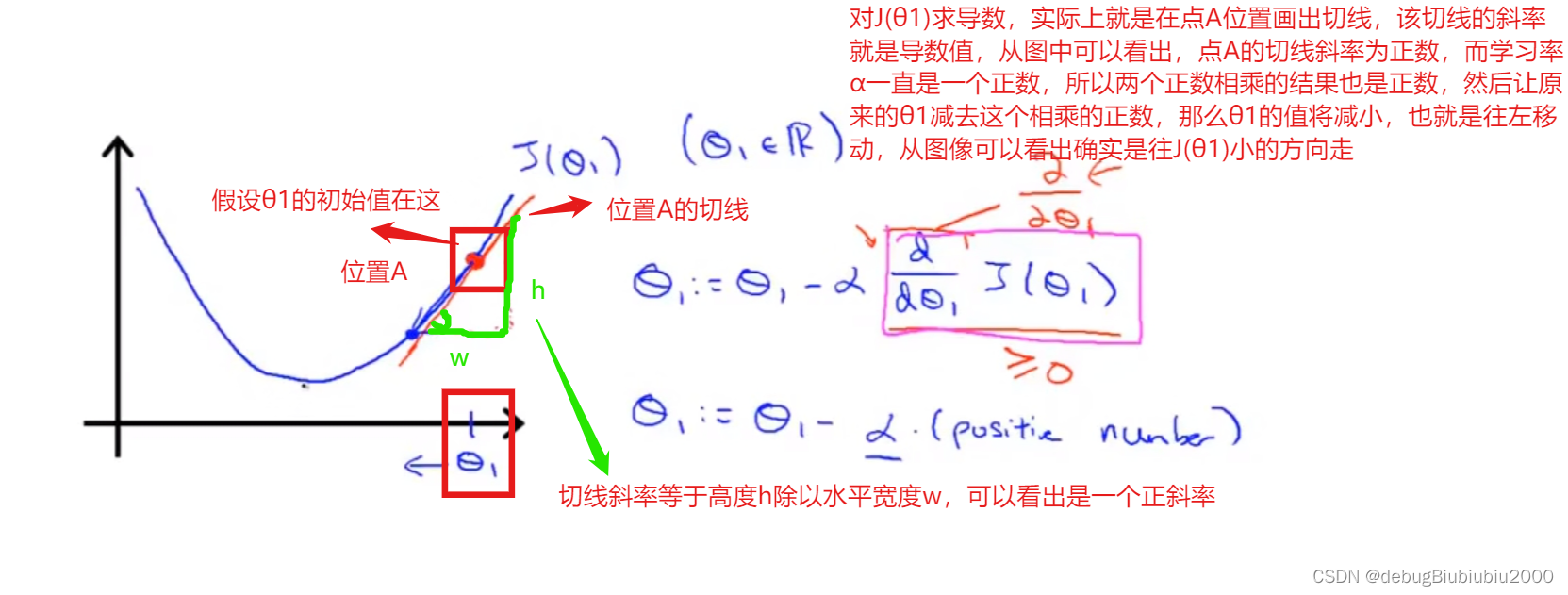
我们再看看另一个位置B的导数，如下

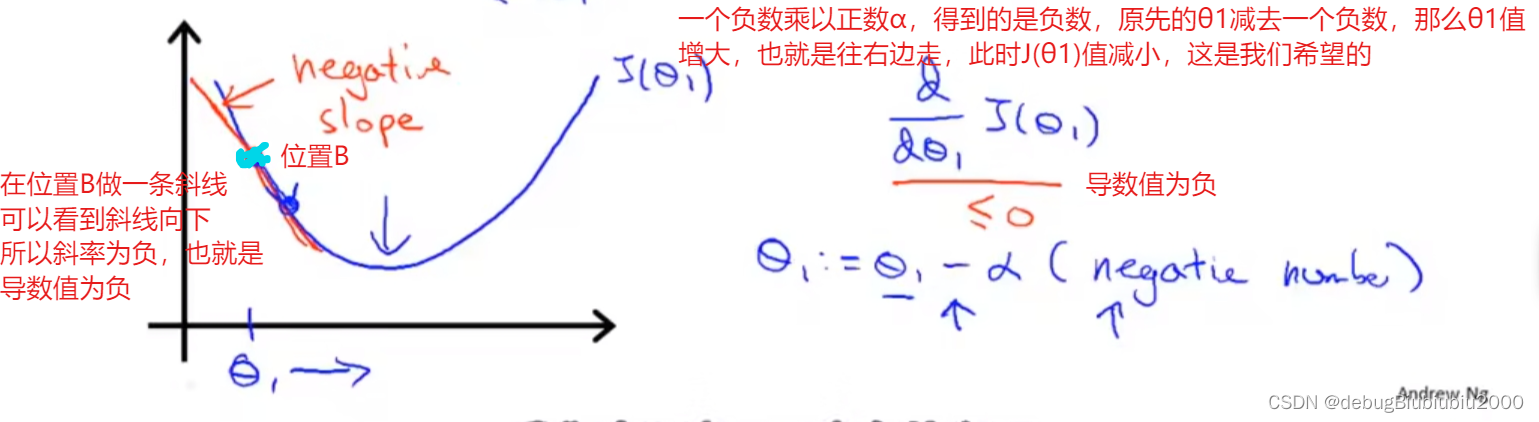
梯度下降算法的运行过程

学习率α大小的影响，如下

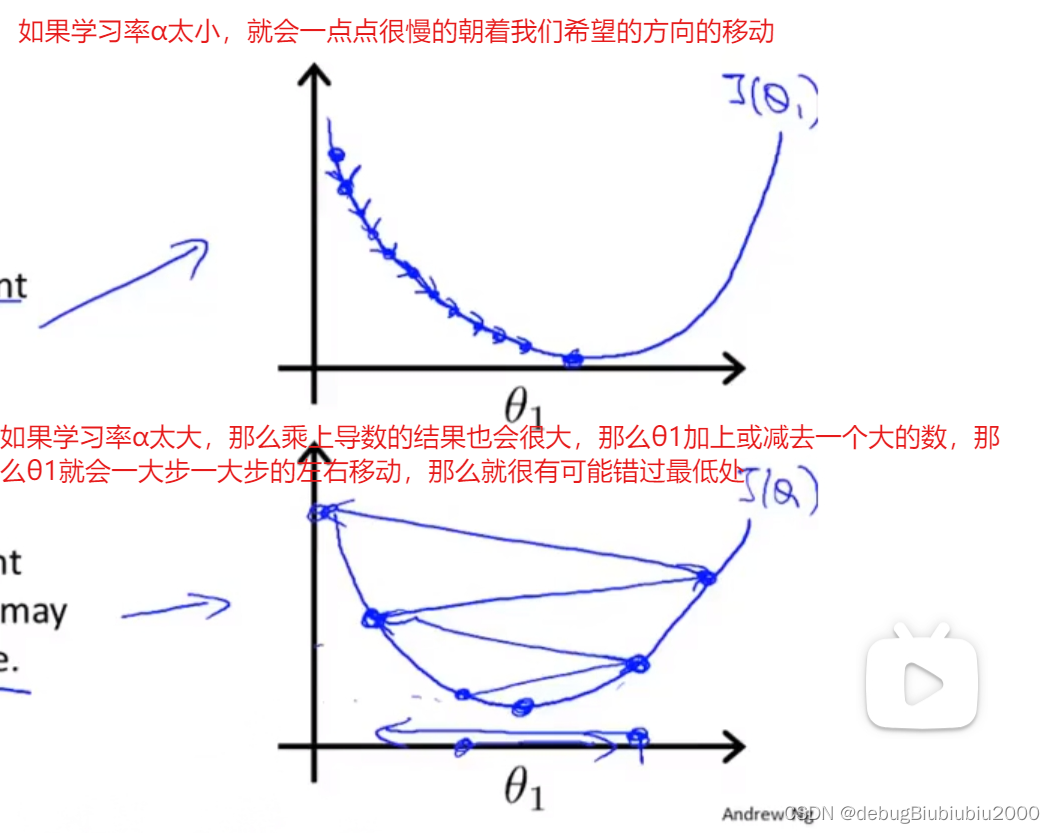
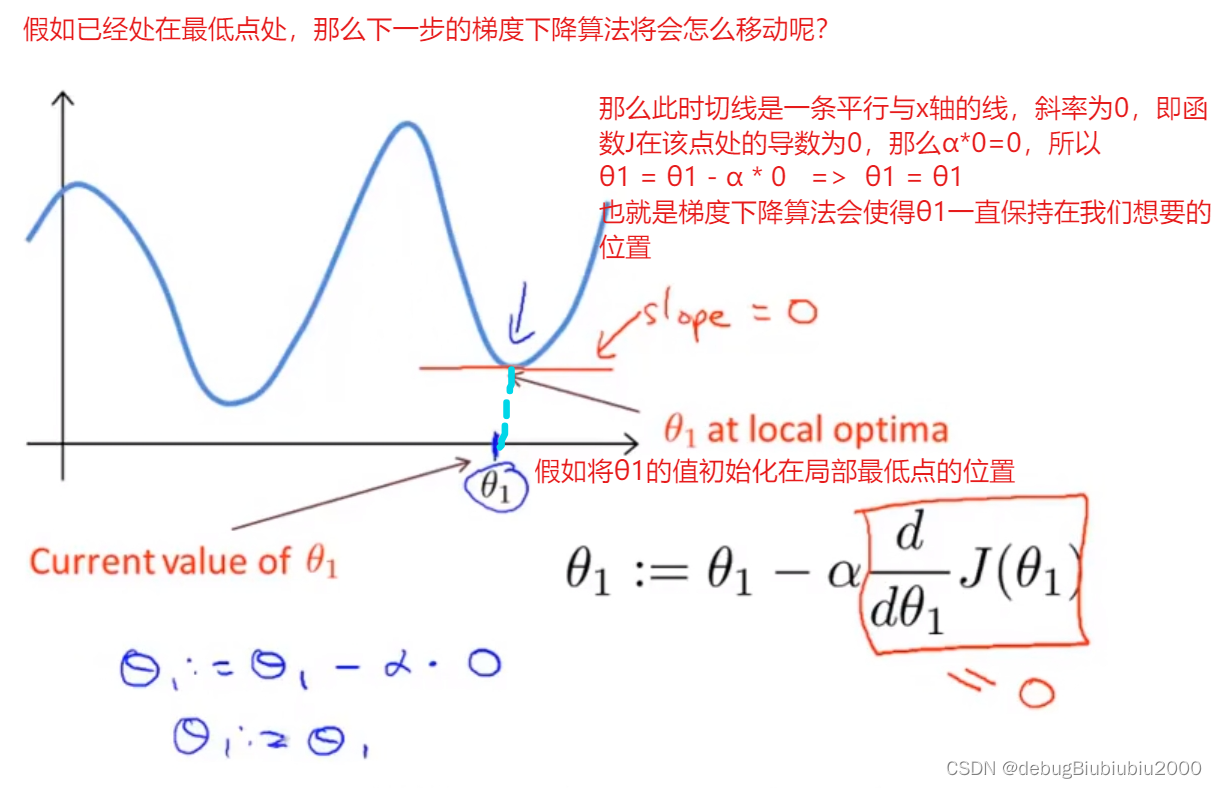
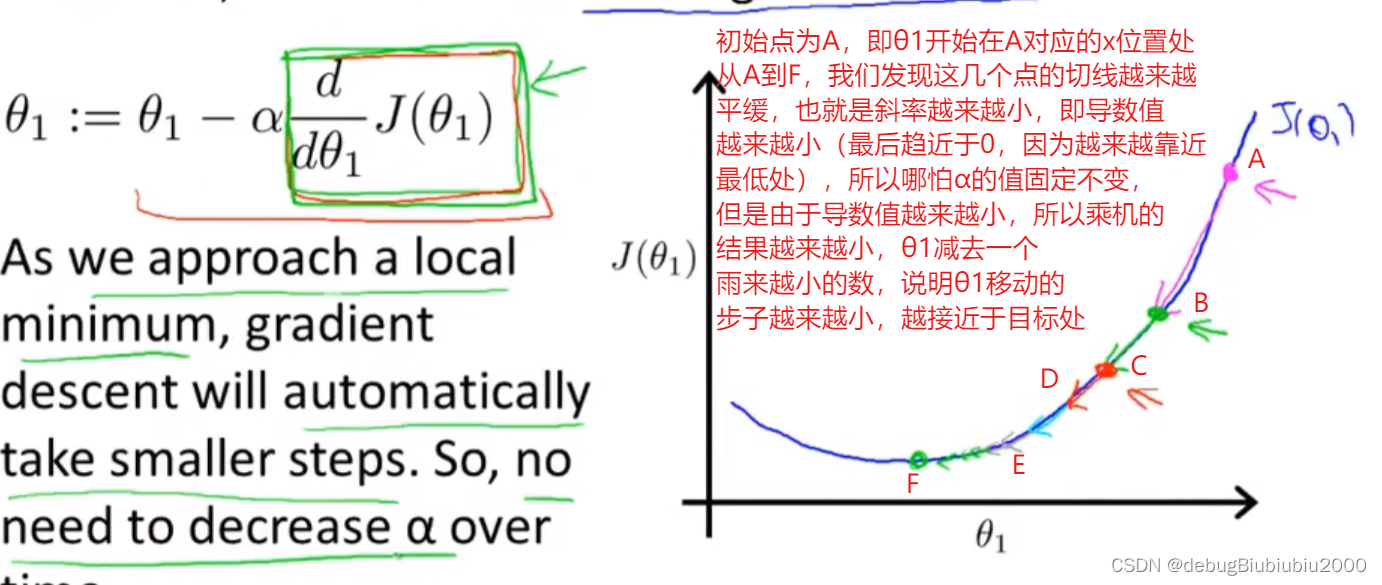
 从上面可以出α是一个固定值，不影响梯度下降算法会自动根据导数值的不同来调整每一步走的步子大小。说到这里，好像也没说α的用处，也没说该如何定义α的值，以及为什么还要乘以α，而不是直接减去导数值？

我看了一下视频弹幕，说我们现在举的都是最简单的函数，但是实际应用中，函数会很复杂，非常有可能是多维的，而且函数不一定连续等等。所以这里就当做是理解梯度下降算法的思想吧。如果后面的视频讲到原因，会做笔记的（B站视频链接 这个专栏里的文章应该都是这个视频的笔记）

梯度下降算法在代价函数中的应用

求梯度下降算法中的导数项

我们先求梯度下降算法中的导数项的值，这里求导数的过程使用了复合函数求导和偏导数这两个知识点。

偏导就是当一个函数中有多个变量，如这里代价函数中有两个变量θ0和θ1，在对其中某一个变量求导数时，将其他变量都视作常数项，如对变量θ0求偏导时，将θ1项都看作是常数项，而复合函数求导法则如下（来自知乎）：

 下图中，隐函数为假设函数h(x) = θ0 + θ1*x，在对θ0求偏导时，h(θ0)` = 1（θ1*x这一项看作常熟项），在对θ1求偏导时，h(θ1)` = x（θ0和x都看作常熟项）

外函数J(h(x)) = (1/2m)[h(x) - y]^2，对J函数偏导时，由于J是复合函数，所以运用复合函数的求导法则，首先J(h(x))` = (1/m)(h(x) - y) （说明：将h(x)看作一个变量，相当于((x-a)²)'=2(x-a)，所以求导之后平方没了，前面的二分之一也消掉了2，这也是为什么之前要写成1/2m的原因），结合上面的h(x)对θ0和θ1的偏导，可以得到图中针对θ0和θ1的导数项的值

将计算得到的导数项代入梯度下降算法公式，如下：

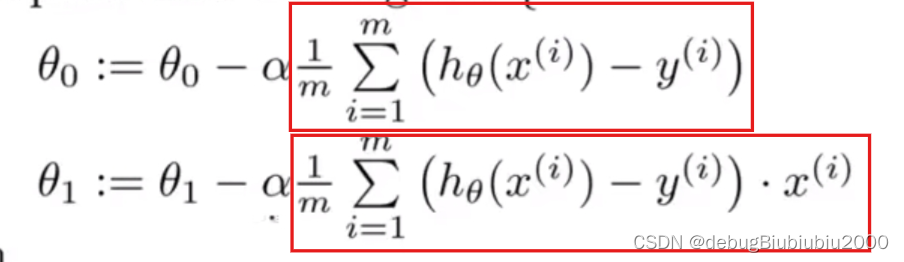
梯度下降函数在线性回归中的具体实现过程

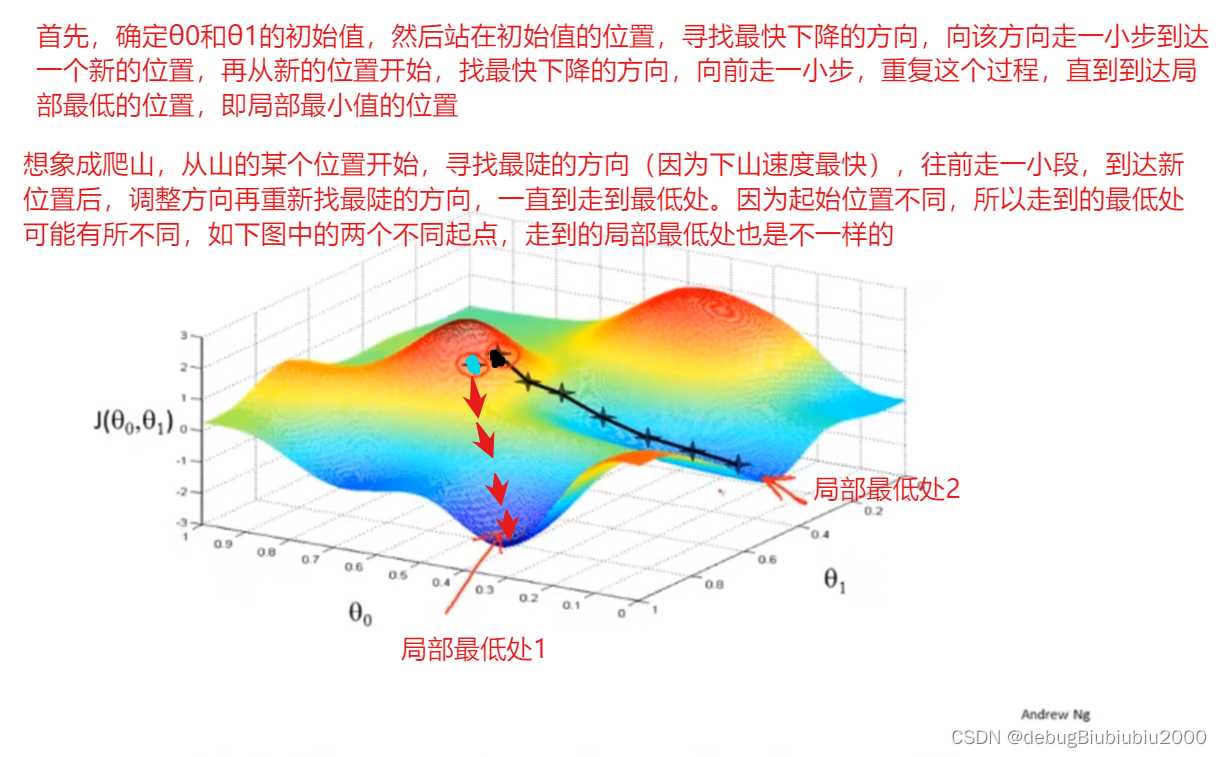
在下面这张图中，从不同的位置出发，即初始化的值不同会得到不同的局部最优解

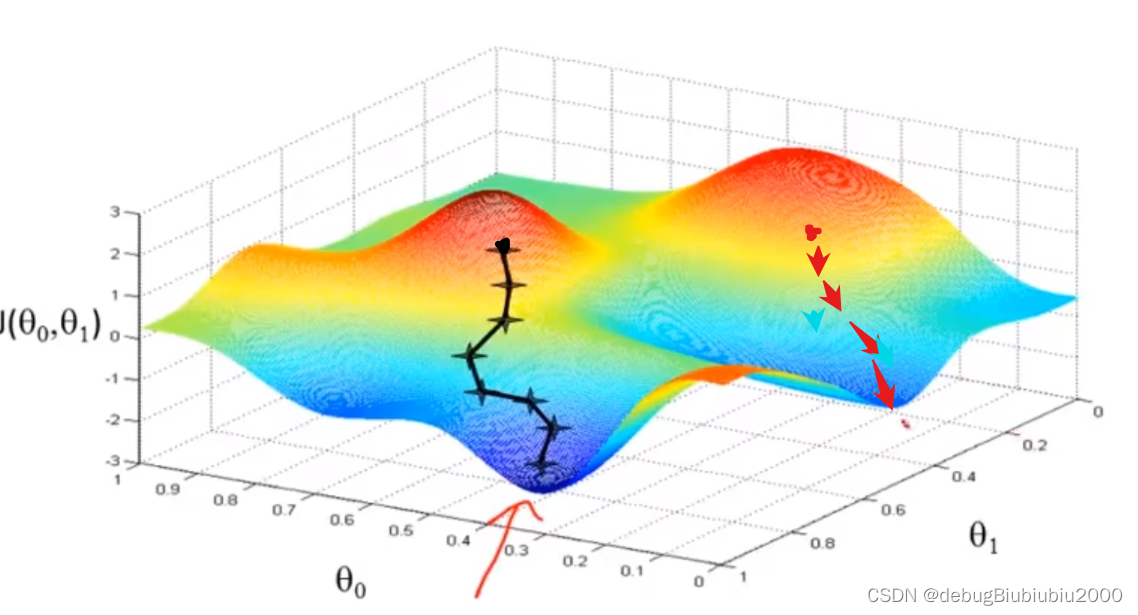
但是我们所举例的房价这一线性回归的例子的代价函数的图像是一个弓状函数（这种称为凸函数，具体的自行百度一下吧，我也不懂），这个函数没有局部最优解，只有全局最优，从图形也可以看出这一点，当计算这种代价函数的梯度下降时，总能得到全局最优解

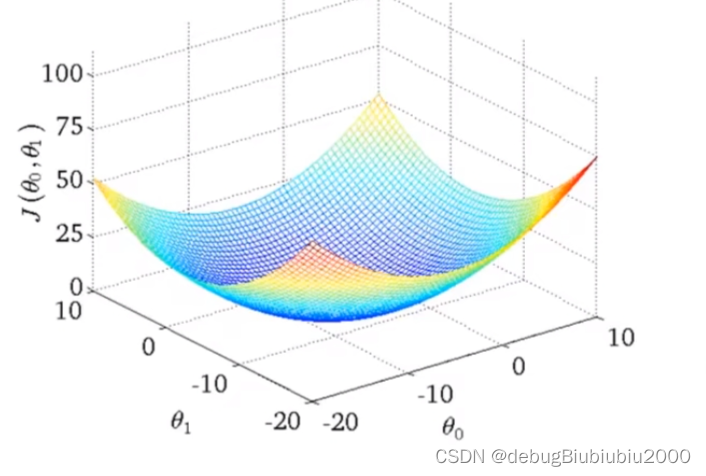
首先，先初始化θ0和θ1的值，一般都初始化为0，在这里为了方便演示，从图中的点开始

 

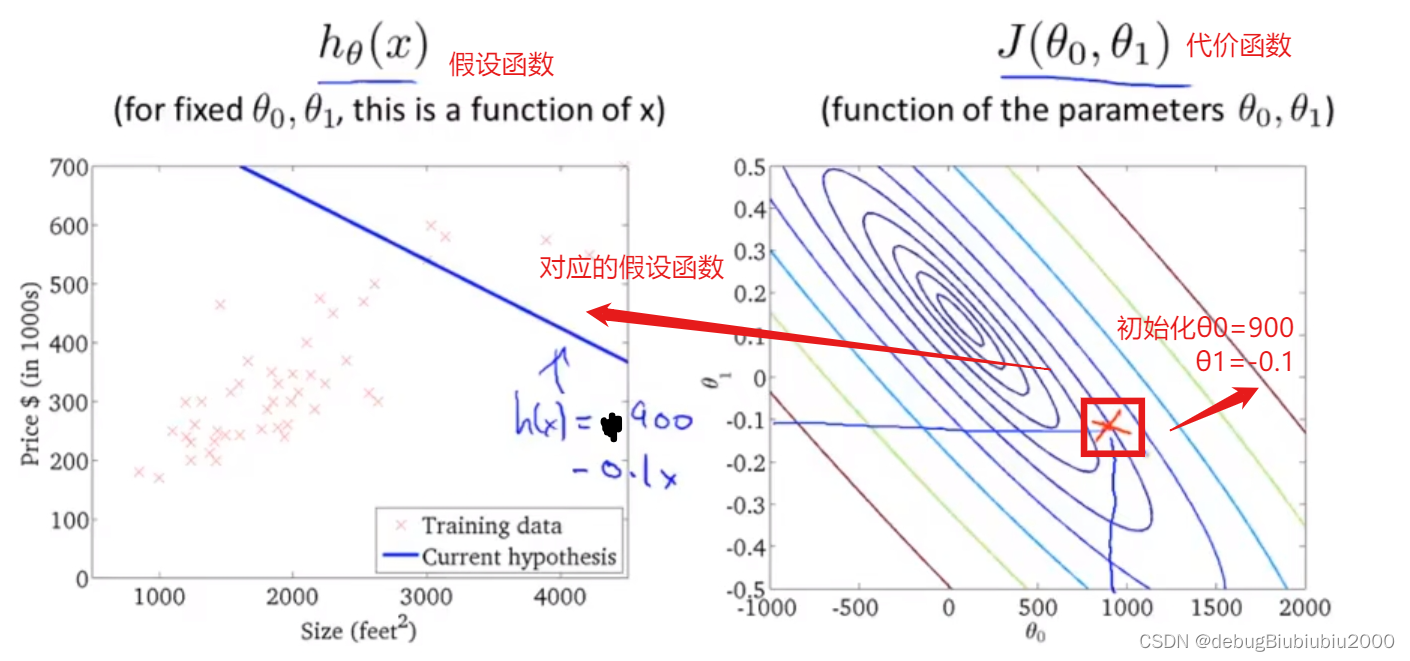
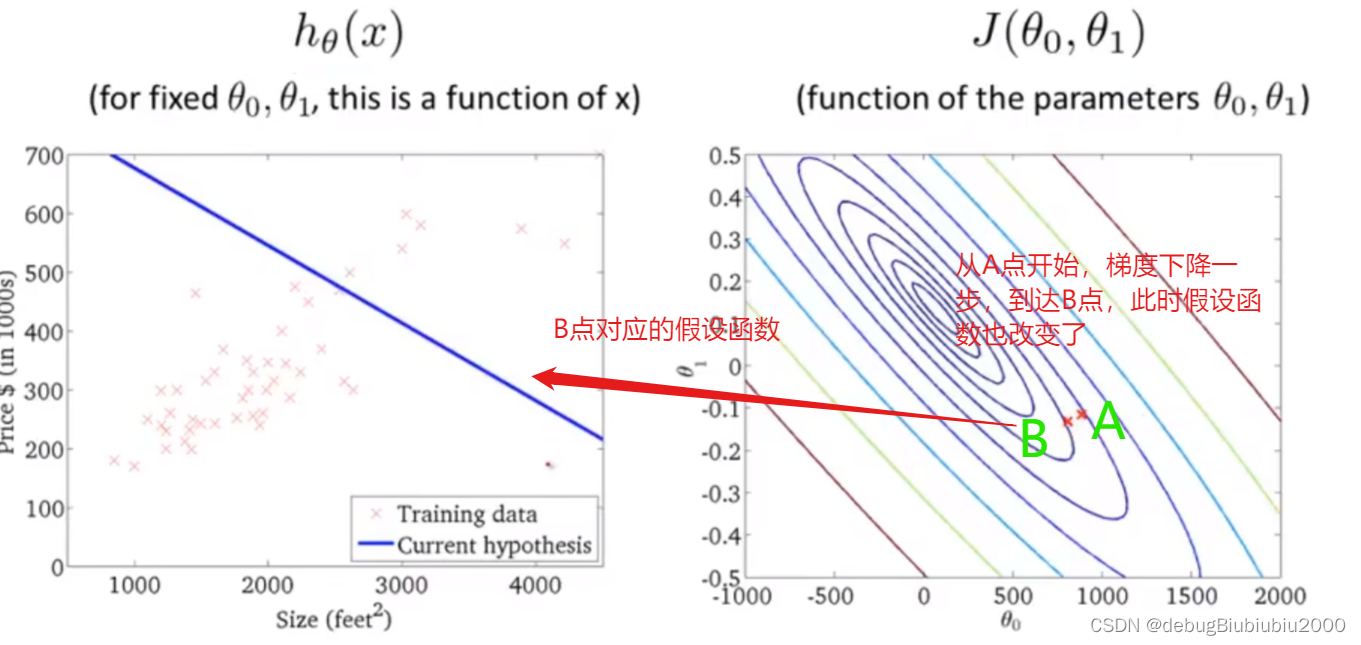
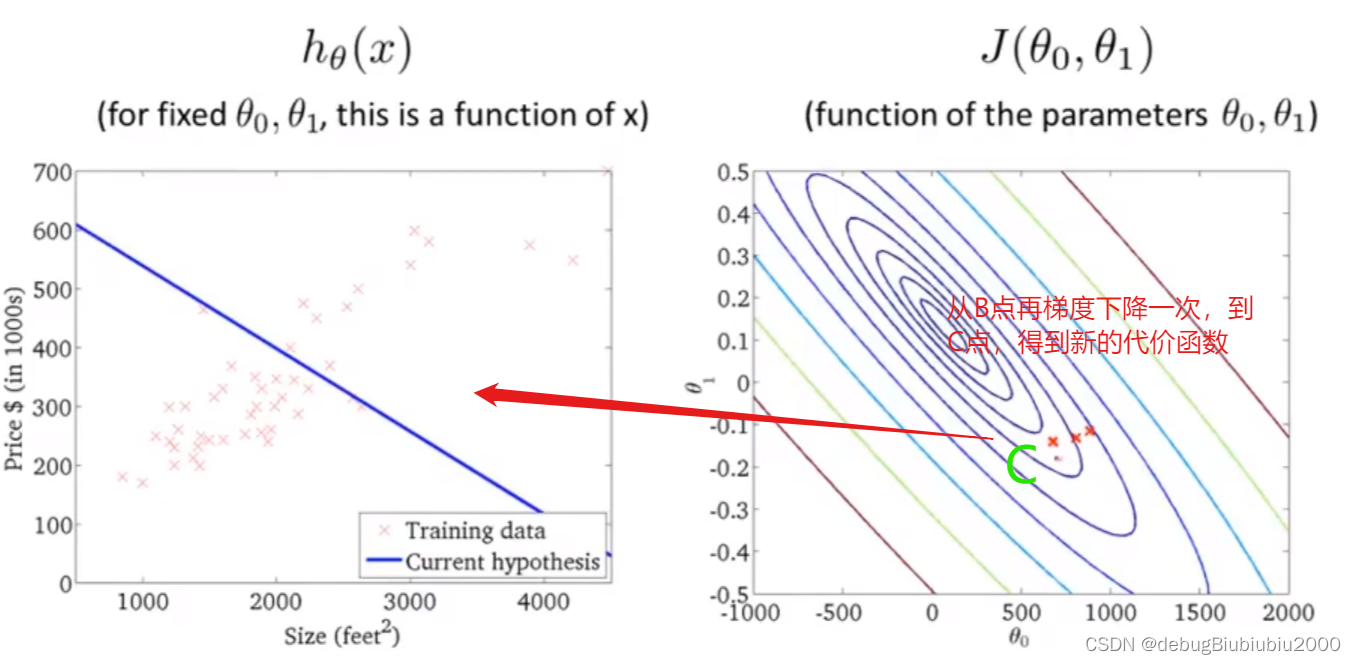
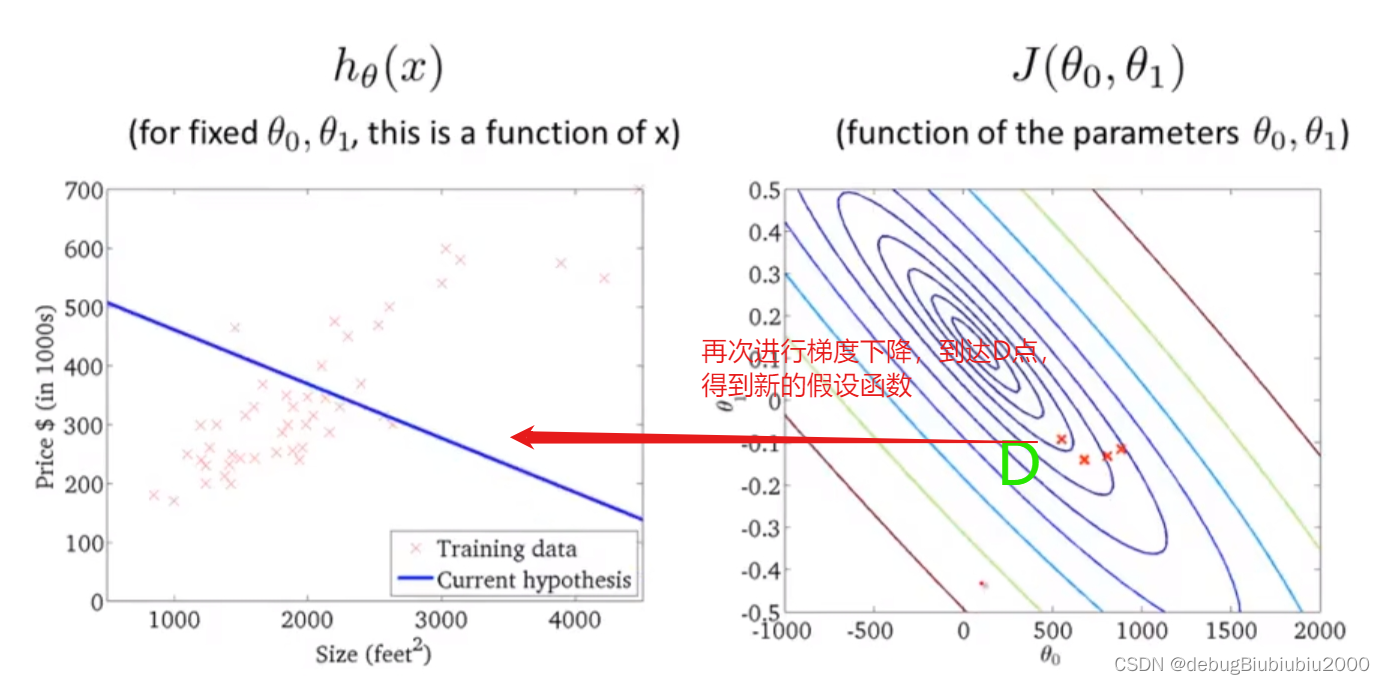
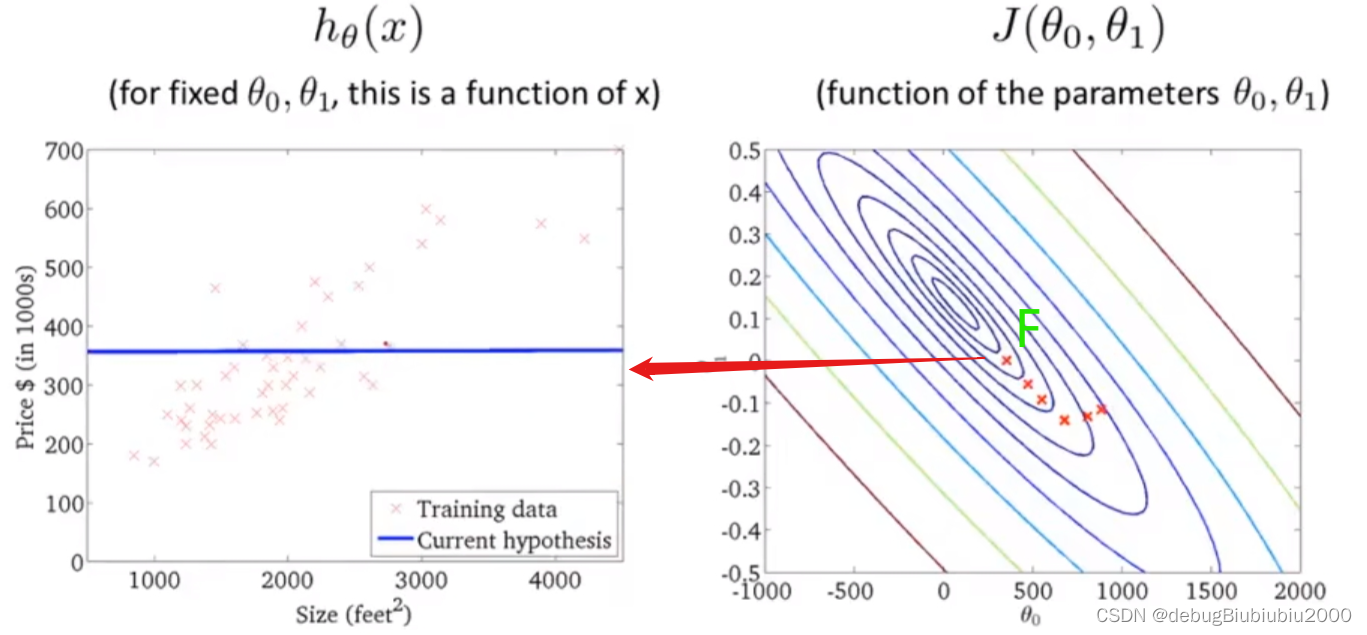
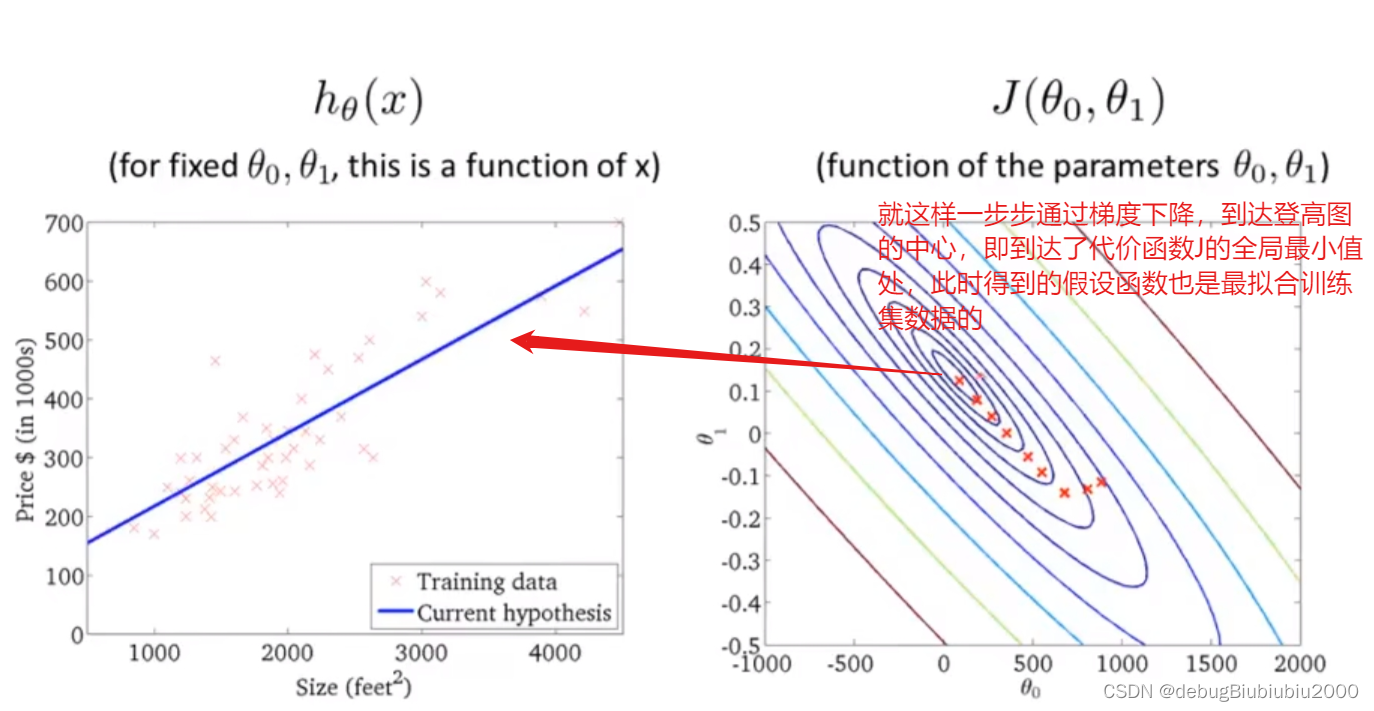上面所展示的梯度下降算法，有时也称为batch梯度下降，从上面的过程中可以看到，batch梯度下降算法每运行一次，即从一个点到另一个点所运行的一次梯度下降，都会遍历训练集中的每个样本（因为在单独的一次梯度下降中，计算偏导时最终都是计算m个样本的总和）.所以batch梯度下降算法每一次都是从整个训练集入手，而还有其他的梯度下降算法，只从训练集的小子集入手