参考视频:https://www.bilibili.com/video/BV1zu411673J/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
参考资料:https://baike.baidu.com/item/%E7%9B%B8%E4%BC%BC%E7%9F%A9%E9%98%B5/10369874?fr=ge_ala
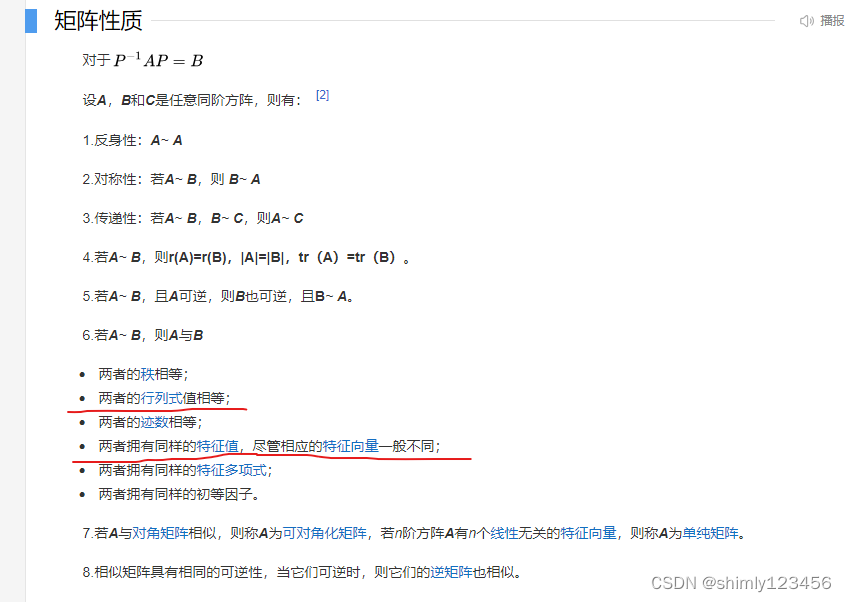
首先看相似矩阵的定义,如下图

这就是相似矩阵的严格定义
还有两个比较关键的性质:
1.相似矩阵的行列式相等
2.相似矩阵的特征值相等
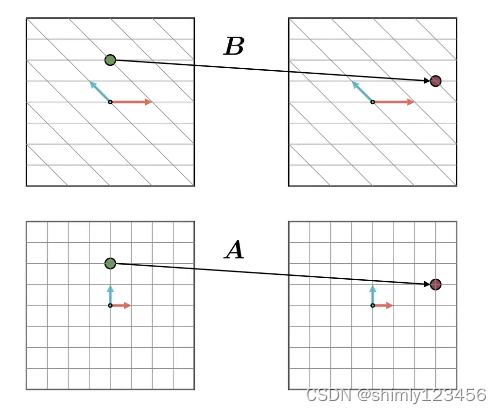
通俗理解,如下图,相似矩阵是 “同一个线性映射,在不同基下的代数表达”
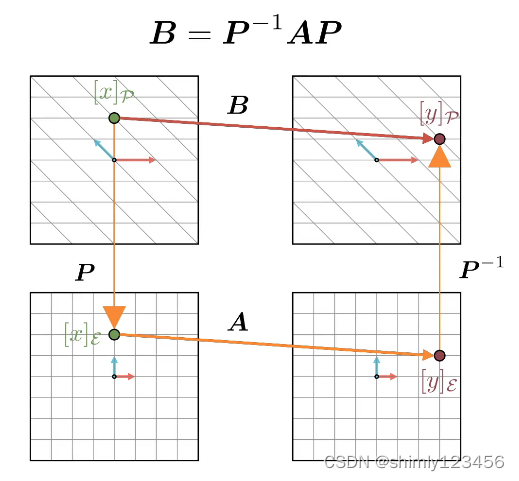
如下图是一个直观的理解:
可以理解为,先把 xp 经过 P 矩阵映射到 xe,然后经过 A 映射到 ye,再由 P^(-1) 映射到 yp 这个过程,可以直接由 B矩阵 的映射得到。
也就是 B = P^(-1) A P
通过相似矩阵,我们可以求解在 不同基 下的旋转矩阵,如下图
这里使用了自由基下的旋转矩阵