物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。
四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼式直升机,从而可知该系统是能够准静态飞行(盘旋飞行和近距离盘旋飞行)的自主飞行器。与传统的旋翼式无人机相比,四旋翼无人机只能通过改变旋翼的 转速来实现各种运动。与传统的直升机那种具有可变倾斜角不同的是,四旋翼无人直升机具有四个倾斜角固定的旋翼,因此结构和动力学特性得到了简化。

四旋翼无人机动态数学模型
任何系统的运动方程,都是针对某一特定的参考坐标系建立的。无人机在本质上属于多体动力学系统。无人机机身的运动可以看成六自由度的刚体运动,包含绕三个轴的转动和重心沿三个轴向的线运动。想要描述无人机的转动,须选用机体坐标系想要描述无人机的位置,须选用地面坐标系。
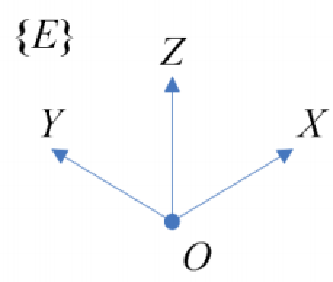
地面坐标系OXYZ
地面坐标系就是一种固定在地球表面的坐标系。首先在地面上选定一个原点 O,使得 X 轴指向地球表面的任意一个方向。Z 轴沿着铅直方向指向天,Y 轴在水平面内与 X 轴垂直,指向通过右手定则来确定。在忽略地球的自转运动和地球质心的 曲线运动时,该地面坐标系可看成是一个惯性坐标系。飞行器的位姿态、速度、角速度等都是相对于这一坐标系来衡量的。
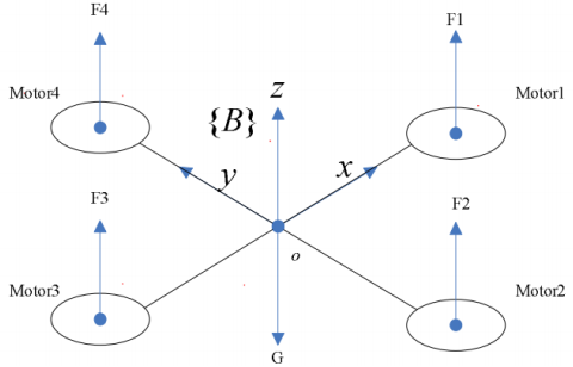
机体坐标系oxyz
坐标系固定在航飞行器上 并遵循右手法则的三维正交直角坐标系称为机体坐标系。原点 o 位于飞行器的质心处, x 轴在飞机的对称平面内,并且平行于飞行器的设计轴线,指向机头前 方。y 轴垂直于机身对称平面,并指向机身右方。z 轴的在飞行器对称平面内, 与 xoy 平面垂直,并指向飞行器的上方。
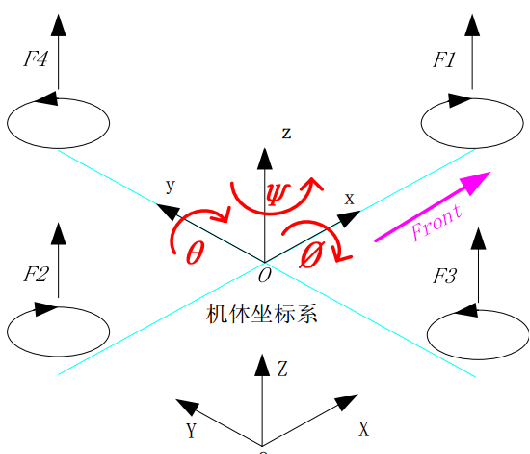
欧拉角
机体坐标系与地面坐标系的关系可以通过三个欧拉角进行表示,分别是俯仰角θ、滚转角Φ和偏航角ψ。
坐标转换矩阵
体坐标系和地面坐标系之间的转换满足下面关系式:
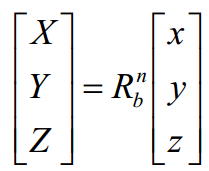
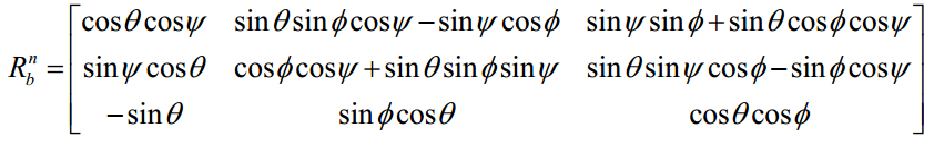
动力学模型的建立
根据牛顿第二定律,有:
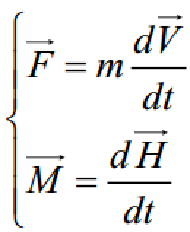

动力学模型的建立

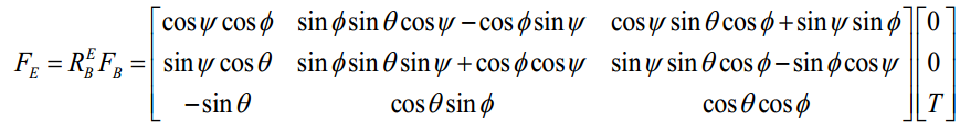
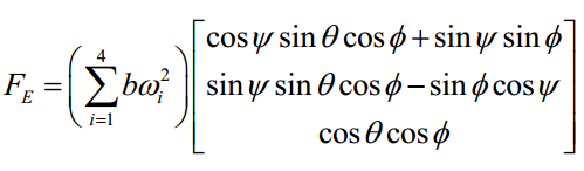
由牛顿第二定律以及飞行器的动力方程,飞行器载体在参考坐标系下的位移方程为:

由此可以得到位置坐标的线性位移方程:
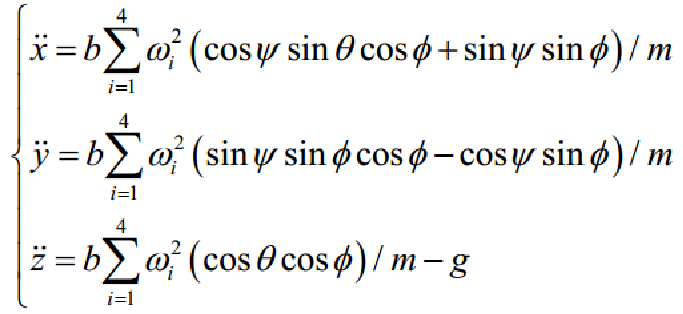
无人机应以动态坐标为基础进行动力学研究。由刚体的欧拉方程,绝对导数在动态坐标下可以表示为:
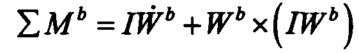
其中(p,q,r分别为机体坐标系上的横滚,俯仰,偏航角速度):
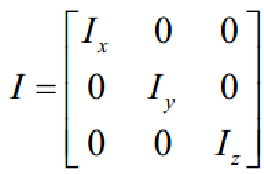
整理得到:
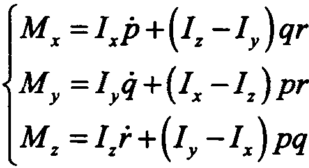
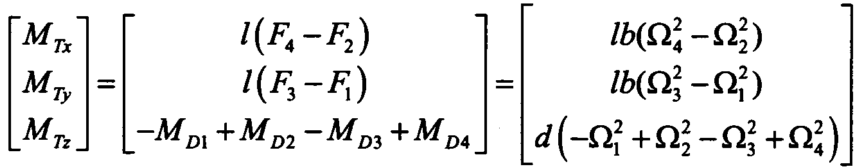
![]()
由欧拉角方程可以飞行器的角运动方程:
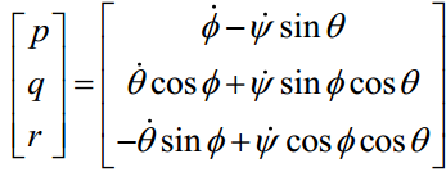
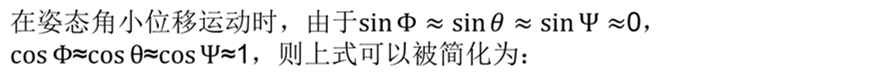

定义:
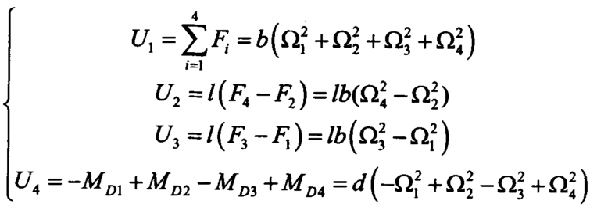
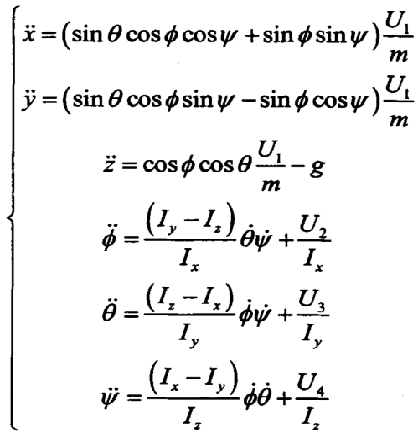
PID控制
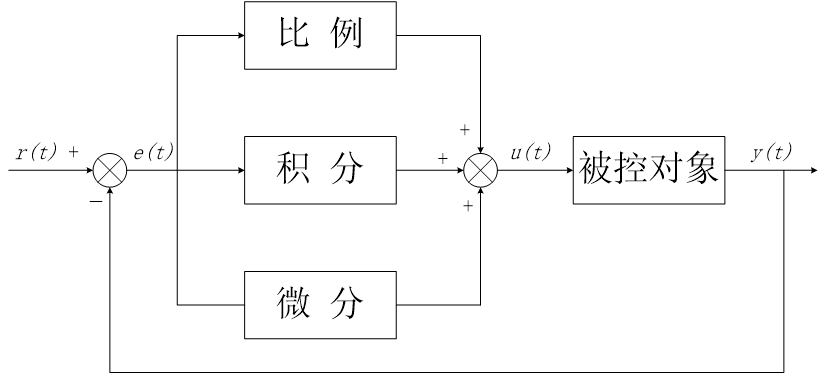
PID控制是一种经典的闭环反馈控制方法,它广泛应用于多种工业控制系统。经典PID控制由比例环节、积分环节和微分环节三部分组成。控制系统以测量值y(t)和设定值r(t)之间的误差值e(t)作为输入量,通过对误差e(t)进行比例、积分和微分运算使控制系统输出量u(t)的误差最小化。
![]()
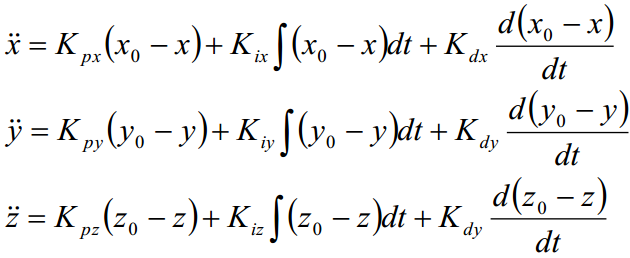
由动力学方程可得俯仰角θ、滚转角Φ的理想值:
![]()
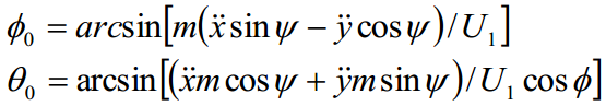
由姿态角PID后得到:
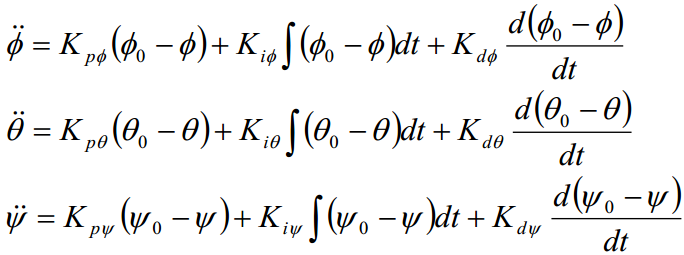


在四旋翼无人机中,无人机的运动主要受到四个电机的旋转速度的影响。每个电机通过旋翼产生升力,进而影响无人机的位置和姿态。因此,物理建模需要建立无人机的位置、速度、加速度、角速度、姿态等运动参数与电机旋转速度之间的关系。
系统集成与验证
系统集成与验证是对四旋翼无人机控制系统建模效果的检验和确认,也是在实际应用中对无人机性能进行评估的重要环节。
在系统集成阶段,需要将物理模型、数学模型和控制算法进行整合,构建完整的四旋翼无人机控制系统。在这个过程中,需要考虑到无人机的硬件限制和实际应用环境,确保系统能够稳定运行。
验证阶段则是对控制系统性能的评估和测试。通过在仿真环境或实际飞行中对无人机的性能进行测试,可以评估控制算法的有效性和稳定性。同时,也可以通过调整控制参数来优化无人机的性能表现。