回归是科研中最常见的统计学研究方法之一，在研究变量间关系方面有着极其广泛的应用。由于其基本假设的限制，包括线性回归及广义线性回归在内的各种常见的回归方法都有三个重大缺陷：(1)对于异常值非常敏感，极少量的异常值可能导致结果产生巨大的误差；(2)对数据的分布有着较为苛刻的要求，如果数据不符合指定的分布，结果同样是不可信的；(3)只能估计因变量的条件均值，不能估计自变量对因变量分位点的不同影响。分位数回归的出现较好的解决了第(1)和第(3)个问题，对不同分布数据也表现非常好的稳定性。分位数回归是一种较新的回归技术，在实践中与普通的线性回归有很大区别，在理论上比线性回归复杂很多。

专题一：线性回归假设与分位数函数

1.线性回归的本质

2.线性回归的基本假设

3.最小二乘法与极大似然法

4.线性回归的推广与分位数函数

专题二：线性分位数回归【代码实践】

1.最小一乘法及其推广

2.分位数回归结果的解释

3.显著性检验

4.分位数回归的拟合优度检验

专题三：贝叶斯分位数回归【代码实践】

1.贝叶斯统计学的基本概念

2.非对称拉普拉斯先验

3.贝叶斯分位数回归

专题四：超越线性分位数回归（一）【代码实践】

1.非线性分位数回归

2.非参数分位数回归

3.广义分位数回归及其贝叶斯版本

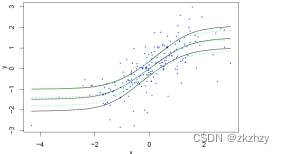
专题五：超越线性分位数回归（二）【代码实践】

1.线性分位数混合效应模型

2.CDF-分位数回归

3.分位数随机森林

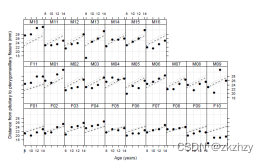
原文链接：

https://mp.weixin.qq.com/s?__biz=MzUyNzczMTI4Mg==&mid=2247618536&idx=8&sn=84ca3cf54ca5d3133a0aa7317e5a98a3&chksm=fa7850d5cd0fd9c32d569cd017965b4459ceff2d10937673ccf22c0bb175ec3d345082d1163d&token=1356914685&lang=zh_CN&scene=21#wechat_redirect