引言

关于最短路问题不论是竞赛、找工作、笔试面试、机试考的都是挺多的，所以还是非常的重要，最重要的就是模板首先背过，然后通过刷题见各种各样的题，具体难点就是如何建图、怎么转换问题，关于最短路问题的基础模板，可以参考我之前写过的博客最短路问题。

---

一、题目描述

题目描述：给一个村庄图，某些村庄中有商店，有多组询问，问某一个村庄到任意一个商店的最短距离是多少。

$有N个村庄，编号1到N。村庄之间有M条无向道路，第i条道路连接村庄a_i和村庄b_i，长度是c_i。$

$所有村庄都是连通的。$

$共有K个村庄有商店，第j个有商店的村庄编号是x_j。$

$然后给出Q个询问，第k个询问给出一个村庄的编号y_k，问该村庄距离最近的商店有多远？$

$输入格式$
$第一行包含两个整数N,M。$
$接下来M行，每行包含三个整数ai,bi,ci，表示第i条道路连接村庄ai和村庄bi，长度是ci。$
$再一行包含整数K。$
$接下来K行，每行包含一个整数xj，表示第j个有商店的村庄编号是xj。$
$再一行包含整数Q。$
$接下来Q行，每行包含一个整数y_k，表示询问编号为y_k的村庄与其距离最近的商店之间的距离。$

$输出格式$
$对于每个询问，输出该询问的结果。$

$数据范围$
$2\le N\le 10^5,N-1\le M\le min(\frac{N(N-1)}{2},10^5),1\le Q\le 10^5,1\le K\le N,1\le c_i\le 10000$
$输入样例：$

7 7
1 2 5
1 4 3
2 3 2
2 5 1
3 6 7
5 6 8
6 7 6
3
7
5
4
7
1
2
3
4
5
6
7

$输出样例：$

3
1
3
0
0
6
0

---

二、解题思路

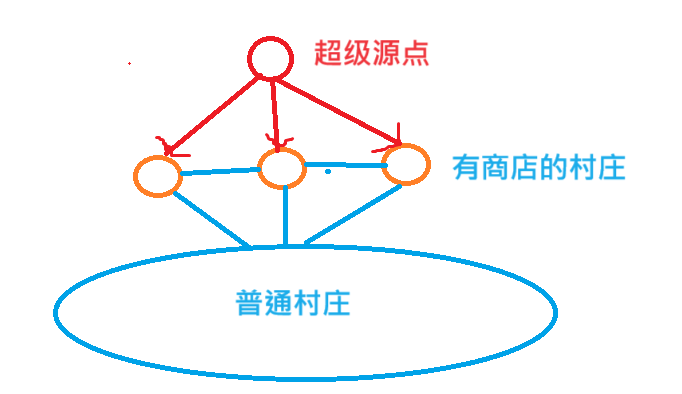
思路：该题是一个多源多汇点问题，我们可以通过增加一个超级源点与每个商店建立连接，权值为 $0$ ，这样村庄到商店的问题就转变为村庄到源点的问题了，即多源单汇点问题，然后我们可以将源点汇点翻转过来，就变成了求超级源点到各个村庄的最短路了，这就跟平常的最短路问题是一样的了， $dist[i]$ 存的就是源点到 $i$ 号点的距离。
注意：这里的超级源点到点的边必须是有向边，因为可能折回来找最近的商店而不是特定的商店。

---

三、示例代码

最短路问题参考博客：最短路问题

#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5+10, M = N * 3;int n, m, k, q;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int spfa()
{memset(dist, 0x3f, sizeof dist);dist[0] = 0;queue<int> q;q.push(0);while(q.size()){auto t = q.front(); q.pop();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){st[j] = true;q.push(j);}}}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(h, -1, sizeof h);cin >> n >> m;while(m--){int a, b, c;cin >> a >> b >> c;add(a,b,c);add(b,a,c);}cin >> k;while(k--){int t; cin >> t;add(0,t,0);}spfa();cin >> q;while(q--){int t; cin >> t;cout << dist[t] << endl;}return 0;
}