目录
5.5 问题五模型的建立与求解
5.5.1 战略级信息化战争评估模型
5.5.2 战略级信息化战争评估模型的验证
6. 模型的评价
6.1 模型的优点
6.2 模型的缺点
参考文献
代码实现
附件1
(1)No_1_result.m 源代码
(2)No_1_figure.m 源代码
附录 2
(1)No_2_Init.m 源代码
(2)No_2_Main.m 源代码
(3)No_2_Beta.m 源代码
(4)No_2_Location_t.m 源代码
(5)No_2_Attack_Or_Not.m 源代码
附录 3
(1)No_3_Init.m 源代码
(2)No_3_Main.m 源代码
(3)No_3_Beta.m 源代码
(4)No_3_Location_t.m 源代码
(5)No_3_Attack_Or_Not.m 源代码
附录 4
(1)No_4_Example.mat 中数据
(2)No_4_Init.m 源代码
(3)No_4_Main.m 源代码
(4)No_4_Membership_1.m 源代码
附录 5
(1)No_5_Init.m 源代码
(2)No_5_Main.m 源代码
本文篇幅较长,分为上下两篇,上篇详见水面舰艇编队防空和信息化战争评估模型
5.5 问题五模型的建立与求解
信息化条件下作战对传统的作战评估模型和作战结果已经产生重要的甚至
某种程度上是决定性的影响。由于经典兰彻斯特方程没有考虑信息对现代战争进
程的影响,若直接采用兰彻斯特方程这种传统的消耗战模型去预测信息化战争的
结果,必然会出现重大误差。
文献 [5] 提出了一种广义兰彻斯特作战模型,该模型 通过将战场感知系数和信
息优势系数引入兰彻斯特方程,描述信息对于信息化战争的影响。 本文参考了
这种模型,并在此基础上,建立了战略级信息化战争评估模型。
5.5.1 战略级信息化战争评估模型
经典兰彻斯特方程根据两种战术情况分为线性律和平方律两种。
兰彻斯特线性律方程如下 




5.5.2 战略级信息化战争评估模型的验证
根据题目附件 B 海湾战争相关资料,得到双方交战兵力数据,其中伊军总
兵力 120 万,美国及多国部队总兵力 76 万。战争中美国及多国部队充分利用其
在信息系统、指挥对抗、系统稳定性上的优势,掌握了制信息权,从而拥有了战
争主动权。
为了检验模型中信息化条件对于战争的影响程度,分别测试两组感知系数,
使用 Matlab 软件对模型进行仿真,并对结果进行比较。(相关 Matlab 源代码,
见附录 5) 

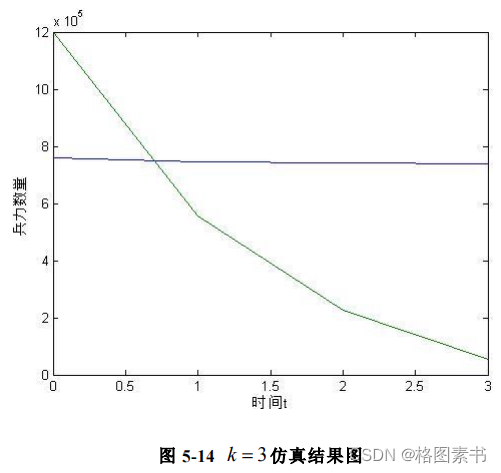



对比分析图 5-13 和图 5-14 可知,当 k = 2 时,作战时间大约为 9 个时间单位,
美国及多国部队兵力损失 86200 个单位;当 k = 3 时,作战时间大约为 3 个时间
单位,美国及多国部队兵力损失 21583 个单位。信息优势从 k = 2 提高到 k = 3 时,
作战时间减少至原来的 13 ,美国及多国部队兵力损失减少到原来的 14 。
综上所述, 在双方兵力、武器性能相当的情况下,获得信息优势的一方能迅
速击败敌方,而且随着信息优势的提高,己方伤亡大幅减小,作战进程大幅加
快。
6. 模型的评价
6.1 模型的优点
对于问题一,指挥舰位于内侧,护卫舰位于外侧,提高了防御纵深。水上舰
艇编队优化模型以使来袭导弹在被发现时刻的位置与指挥舰的最短距离最长为
目标,而不是以警戒幕面积最大为优化目标,简化了模型计算的复杂程度,提高
了模型的可行性。
对于问题二和问题三,从来袭导弹的运动轨迹、防空导弹的拦截过程、舰艇
编队的火力分配等三个角度进行问题的分析与求解。尤其是构建了基于
Multi-Agent 的火力分配优化模型,不仅适用于单批次或多批次单方向来袭导弹
拦截任务的火力分配,还适用于多批次多方向来袭导弹拦截任务的火力分配,具
有较强的实际意义。
对于问题四,建立了适用于只有少量训练样本的模糊识别模型,并通过蒙
特·卡罗方法确定了较优的参数,模型识别的准确率达到 73.33% ,具有一定可
靠性。
对于问题五,采用定性与定量相结合的思想,在兰彻斯特方程基础上,引入
战场感知系数和信息优势系数,建立了战略级信息化战争评估模型,计算出了在
信息化战争中,信息对于战争双方的影响。
6.2 模型的缺点
对于问题一,水上舰艇编队优化模型未考虑电子干扰、近程火炮(包括密集
阵火炮)等拦截手段以及来袭导弹“二次捕捉”能力等因素对编队队形的影响。
对于问题五,模型的计算是基于作战双方的实力进行的。本文由于数据不全,
只考虑了作战双方的兵力数量,并没有考虑能够影响作战双方实力的武器装备等
因素。
参考文献
[1] 闫国玉 , 郭万海 , 李国建 . 水面舰艇编队防空体系构建及其效能研究 [J]. 火力与指挥控
制 , 2005, 30( 增刊 ).
[2] 周晶 , 宋辉 , 王秀森 , 等 . 基于 Multi-Agent 的编队对空防御方法 [J]. 兵工自动化 , 2011,
30(9).
[3] 汪天飞 , 邹进 , 张军 . 数学建模与数学实验 [M]. 北京 : 科学出版社 , 2013.
[4] 李志强 . 复杂系统与战争模拟研究 [M]. 北京 : 国防大学出版社 , 2011.
[5] 吴俊 , 杨峰 , 梁彦 , 等 . 面向信息化战争的广义兰切斯特作战模型 [J]. 火力与指挥控制 ,
2010, 35(2).
代码实现
附件1
(1)No_1_result.m 源代码
clc;
clear all;
x=42.878;
% - A 点距离
L_A=sqrt((20*sind(10)+x*cosd(10))^2+(20*cosd(10)-x*sind(10))^2)
% - A 点角度
T_A=atand((20*cosd(10)-x*sind(10))/(20*sind(10)+x*cosd(10)))+30
% - B 点距离
L_B=sqrt((20)^2+(sqrt(1600-(20*sind(10)+x*cosd(10)-20)^2)+20*cosd(10)-x*sind(10))^2)
% - B 点角度
T_B=atand((sqrt(1600-(20*sind(10)+x*cosd(10)-20)^2)+20*cosd(10)-x*sind(10))/20)+30
% - C 点距离
L_C=L_B
% - C 点角度
T_C=T_B+2*atand(20/(sqrt(1600-(20*sind(10)+x*cosd(10)-20)^2)+20*cosd(10)-x*sind(10)))
% - D 点距离
L_D=L_A
% - D 点角度
T_D=T_A+2*atand((20*sind(10)+x*cosd(10))/(20*cosd(10)-x*sind(10)))(2)No_1_figure.m 源代码
clc;
clear all;
x_min=16.782;
x_max=56.782;
x_equal=42.878;
x1=x_min:0.05:x_equal;
x2=x_equal:0.05:x_max;
y1=x1;
y2=sqrt(-0.9702*x2.^2 + 32.5444*x2 + 1327.0896)-0.174*x2+19.7;
figure;
plot(x1,y1);
hold on;
plot(x2,y2);
grid on;附录 2
(1)No_2_Init.m 源代码
clc;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 设定运动参数
% - 单位(m/s)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
v0=8.231; %指挥舰运动速度
v1=306; %来袭导弹运动速度
v2=816; %防空导弹运动速度
Pmax=42878; %导弹群初始位置与指挥舰距离,单位 m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 设定仿真参数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
t=0; %仿真时钟
step=0.1; %设定时钟步长,单位 s
flag=0; %仿真控制标志位,为 1 时仿真结束(来袭导弹群距离指挥舰距离≤10 公里)
beat=0; %拦截次数
eggs=No_2_Location_t(Pmax,v0,v1,0); %来袭导弹群初始位置
dmin=10000; %仿真结束判断阈值,10000m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 以指挥舰为远点,正北方向为 y 轴正方向,建立指标坐标系
% - 单位(m)!!!!!!!
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 变换单位(m-km)
Pmax=Pmax/1000;
% - A 点距离
L_A=sqrt((20*sind(10)+Pmax*cosd(10))^2+(20*cosd(10)-Pmax*sind(10))^2);
% - A 点角度
T_A=atand((20*cosd(10)-Pmax*sind(10))/(20*sind(10)+Pmax*cosd(10)))+30;
% - B 点距离
L_B=sqrt((20)^2+(sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind(10))
^2);
% - B 点角度
T_B=atand((sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind(10))/20)+3
0;
% - C 点距离
L_C=L_B;
% - C 点角度
T_C=T_B+2*atand(20/(sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind
(10)));
% - D 点距离
L_D=L_A;
% - D 点角度
T_D=T_A+2*atand((20*sind(10)+Pmax*cosd(10))/(20*cosd(10)-Pmax*sind(10)));
% - 变换单位(km-m)
Pmax=Pmax*1000;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 构建舰队模型 [ 编号 , x 坐标 , y 坐标 , beta , l , 状态标志 ]
% - 指挥舰编号为 0,护卫舰编号为 1-4
% - beta 为【舰船与来袭导弹初始位置连线】与【来袭导弹飞行方向】的夹角
% - l 为舰船与来袭导弹初始位置距离
% - 状态标志=0 表示可以发射防空导弹
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
ships=[ 0 , 0 , 0 , 0 , 0 , 0 ;1 , L_A*sind(T_A)*1000 , L_A*cosd(T_A)*1000 , 0 , 0 , 0 ;2 , L_B*sind(T_B)*1000 , L_B*cosd(T_B)*1000 , 0 , 0 , 0 ;3 , L_C*sind(T_C)*1000 , L_C*cosd(T_C)*1000 , 0 , 0 , 0 ;4 , L_D*sind(T_D)*1000 , L_D*cosd(T_D)*1000 , 0 , 0 , 0 ];
% - 计算 beta,beta
for i=1:1:5ships(i,4)=No_2_Beta(ships(i,2:3),eggs);ships(i,5)=sqrt(sum((ships(i,2:3)-eggs).^2));
end(2)No_2_Main.m 源代码
% - 初始化
No_2_Init;
% - 开始仿真
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
disp(['--> 【开始仿真】']);
disp(['-->']);
38
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
tic;
while flag==0% - step1:计算导弹群距离指挥舰距离eggs_now=No_2_Location_t(Pmax,v0,v1,t); %导弹群当前位置d=sqrt(sum(eggs_now.^2)); %导弹群与指挥舰当前距离 %disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰 : ',num2str(d/1000),'
km']);%pause(0.05);% - step2:判断仿真是否终止% - 仿真继续if d>999 %仿真继续% - step3:对 Multi-Agent 进行任务分配for i=1:1:5% - step4:进行状态轮询if ships(i,6)==0% - step:5 计算攻击条件attack_flag=No_2_Attack_Or_Not(Pmax,ships(i,2:5),v0,v1,v2,t); %attack_flag=[flag,det_t];if attack_flag(1)==1 %可以发射防空导弹ships(i,6)=7+attack_flag(2);%ships(i,6)=7;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船发起拦截']);%pause(0.05);endelseships(i,6)=ships(i,6)-step;if ships(i,6)<=0ships(i,6)=0;beat=beat+1;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船拦截完成,总拦截数:',num2str(beat)]);%pause(0.05);% - 重复 step:5 计算攻击条件attack_flag=No_2_Attack_Or_Not(Pmax,ships(i,2:5),v0,v1,v2,t); %attack_flag=[flag,det_t];if attack_flag(1)==1 %可以发射防空导弹ships(i,6)=7+attack_flag(2);%ships(i,6)=7;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船发起拦截']);%pause(0.05);endendendend% - 更新仿真时钟t=t+step;% - 仿真终止else flag=1;end
end
disp(['-->']);
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
disp(['--> 【仿真结束】']);
disp(['-->']);
disp(['--> 总计拦截来袭导弹 ',num2str(beat),' 批']);
disp(['-->']);
disp(['--> 仿真用时: ',num2str(toc),' s']);
disp(['--> ------------------------------------------------------------']);(3)No_2_Beta.m 源代码
function beta=No_2_Beta(X_ship,egg)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - beta:【舰船与来袭导弹初始位置连线】与【来袭导弹飞行方向】的夹角
% - X_ship=[x,y]:目标舰坐标
% - egg=[x,y]:来袭导弹初始位置坐标
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
cos_beta=(sum(egg.^2)+sum((X_ship-egg).^2)-sum(X_ship.^2))/(2*sqrt(sum(egg.^2))*sqrt(sum((
X_ship-egg).^2)));
beta=acosd(cos_beta);(4)No_2_Location_t.m 源代码
function Location=No_2_Location_t(Pmax,v0,v1,t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - Location=[xt,yt]:t 时刻导弹的位置
% - Pmax
% - v0:指挥舰速度
% - v1:来袭导弹速度
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 计算导弹相对于指挥舰速度的 x 轴分量
vx=v1*cosd(220.5249-180)+v0*sind(200-180); %235.4130% - 计算导弹相对于指挥舰速度的 y 轴分量
vy=v1*sind(220.5249-180)+v0*cosd(200-180); %206.5668
% - 导弹相对运动方向与 x 轴夹角
A=atand(vy/vx);
% - 计算 xt
xt=vx*t-Pmax*cosd(A);
% - 计算 yt
yt=vy*t-Pmax*sind(A);
% - 整理输出
Location=[xt,yt];(5)No_2_Attack_Or_Not.m 源代码
function attack_flag=No_2_Attack_Or_Not(Pmax,ship,v0,v1,v2,t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - attack_flag=[flag,det_t]
% - flag=1:表示可以发射防空导弹
% - det_t:拦截冻结时间
% - ship=[x,y,beta,l]
% - v0:指挥舰速度
% - v1:来袭导弹速度
% - v2:防空导弹速度
% - t:仿真时钟当前值
% 注:导弹发射准备时间为 7 秒
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 构建方程参数
a=v1^2-v2^2;
b=2*(v1^2)*(t+7)-2*cosd(ship(3))*v1*ship(4);
c= ship(4)^2 + ((t+7)^2)*(v1^2) - 2*cosd(ship(3))*v1*ship(4)*(t+7);
% - 构建方程
str=['(',num2str(a),')*x^2+(',num2str(b),')*x+(',num2str(c),')=0'];
% - 求解
x=solve(str);
x=double(x);
% - 分析结果
if x(1)<0det_t=x(2);
elseif x(2)<0det_t=x(1);elsedet_t=min([x(1),x(2)]);
end
% - 判断攻击条件
flag=1;
% - 条件 1:是否超出防空导弹射程
if det_t*v2>=80000flag=0;
end
if det_t*v2<=10000flag=0;
end
% - 条件 2:拦截地点距离指挥舰是否太近
attack_Location=No_2_Location_t(Pmax,v0,v1,t+det_t);
if sqrt(sum(attack_Location.^2))<10000 || t+det_t>115flag=0;
end
% - 整理输出
attack_flag=[flag,det_t];附录 3
(1)No_3_Init.m 源代码
clc;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 设定运动参数
% - 单位(m/s)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
v0=8.231; %指挥舰运动速度
v1=306; %来袭导弹运动速度
v2=816; %防空导弹运动速度
Pmax=200000; %导弹群初始位置与指挥舰距离,单位 m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 设定仿真参数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
t=0; %仿真时钟
step=1; %设定时钟步长,单位 s
flag=0; %仿真控制标志位,为 1 时仿真结束(来袭导弹群距离指挥舰距离≤10 公里)
beat=0; %拦截次数
eggs=No_3_Location_t(Pmax,v0,v1,0); %来袭导弹群初始位置
dmin=999; %仿真结束判断阈值,10000m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 以指挥舰为远点,正北方向为 y 轴正方向,建立指标坐标系
% - 单位(m)!!!!!!!
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 变换单位(m-km)
Pmax=42878/1000;
% - A 点距离
L_A=sqrt((20*sind(10)+Pmax*cosd(10))^2+(20*cosd(10)-Pmax*sind(10))^2);
% - A 点角度
T_A=atand((20*cosd(10)-Pmax*sind(10))/(20*sind(10)+Pmax*cosd(10)))+30;
% - B 点距离
L_B=sqrt((20)^2+(sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind(10))
^2);
% - B 点角度
T_B=atand((sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind(10))/20)+3
0;
% - C 点距离
L_C=L_B;
% - C 点角度
T_C=T_B+2*atand(20/(sqrt(1600-(20*sind(10)+Pmax*cosd(10)-20)^2)+20*cosd(10)-Pmax*sind
(10)));
% - D 点距离
L_D=L_A;
% - D 点角度
T_D=T_A+2*atand((20*sind(10)+Pmax*cosd(10))/(20*cosd(10)-Pmax*sind(10)));
% - 变换单位(km-m)
Pmax=200000;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 构建舰队模型 [ 编号 , x 坐标 , y 坐标 , beta , l , 状态标志 ]
% - 指挥舰编号为 0,护卫舰编号为 1-4
% - beta 为【舰船与来袭导弹初始位置连线】与【来袭导弹飞行方向】的夹角
% - l 为舰船与来袭导弹初始位置距离
% - 状态标志=0 表示可以发射防空导弹
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
ships=[ 0 , 0 , 0 , 0 , 0 , 0 ;1 , L_A*sind(T_A)*1000 , L_A*cosd(T_A)*1000 , 0 , 0 , 0 ;2 , L_B*sind(T_B)*1000 , L_B*cosd(T_B)*1000 , 0 , 0 , 0 ;3 , L_C*sind(T_C)*1000 , L_C*cosd(T_C)*1000 , 0 , 0 , 0 ;4 , L_D*sind(T_D)*1000 , L_D*cosd(T_D)*1000 , 0 , 0 , 0 ];
% - 计算 beta,beta
for i=1:1:5ships(i,4)=No_3_Beta(ships(i,2:3),eggs);ships(i,5)=sqrt(sum((ships(i,2:3)-eggs).^2));
end
(2)No_3_Main.m 源代码
% - 初始化
No_3_Init;
% - 开始仿真
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
disp(['--> 【开始仿真】']);
disp(['-->']);
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
tic;
while flag==0% - step1:计算导弹群距离指挥舰距离eggs_now=No_3_Location_t(Pmax,v0,v1,t); %导弹群当前位置d=sqrt(sum(eggs_now.^2)); %导弹群与指挥舰当前距离 %disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰 : ',num2str(d/1000),'
km']);%pause(0.05);% - step2:判断仿真是否终止% - 仿真继续if d>dmin %仿真继续% - step3:对 Multi-Agent 进行任务分配for i=1:1:5% - step4:进行状态轮询if ships(i,6)==0% - step:5 计算攻击条件attack_flag=No_3_Attack_Or_Not(Pmax,ships(i,2:5),v0,v1,v2,t); %attack_flag=[flag,det_t];if attack_flag(1)==1 %可以发射防空导弹ships(i,6)=7+attack_flag(2);%ships(i,6)=7;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船发起拦截']);%pause(0.05);endelseships(i,6)=ships(i,6)-step;if ships(i,6)<=0ships(i,6)=0;beat=beat+1;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船拦截完成,总拦截数:',num2str(beat)]);%pause(0.05);% - 重复 step:5 计算攻击条件attack_flag=No_3_Attack_Or_Not(Pmax,ships(i,2:5),v0,v1,v2,t); %attack_flag=[flag,det_t];if attack_flag(1)==1 %可以发射防空导弹ships(i,6)=7+attack_flag(2);%ships(i,6)=7;disp(['--> t= ',num2str(t),' s , 来袭导弹距离指挥舰: ',num2str(d/1000),'
km , ',num2str(i),' 号舰船发起拦截']);%pause(0.05);endendendend% - 更新仿真时钟t=t+step;% - 仿真终止else flag=1;end
end
disp(['-->']);
disp(['--> ------------------------------------------------------------']);
disp(['-->']);
disp(['--> 【仿真结束】']);
disp(['-->']);
disp(['--> 总计拦截来袭导弹 ',num2str(beat),' 批']);
disp(['-->']);
disp(['--> 仿真用时: ',num2str(toc),' s']);
disp(['--> ------------------------------------------------------------']);
(3)No_3_Beta.m 源代码
function beta=No_3_Beta(X_ship,egg)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - beta:【舰船与来袭导弹初始位置连线】与【来袭导弹飞行方向】的夹角
% - X_ship=[x,y]:目标舰坐标
% - egg=[x,y]:来袭导弹初始位置坐标
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
cos_beta=(sum(egg.^2)+sum((X_ship-egg).^2)-sum(X_ship.^2))/(2*sqrt(sum(egg.^2))*sqrt(sum((
X_ship-egg).^2)));
beta=acosd(cos_beta);
(4)No_3_Location_t.m 源代码
function Location=No_3_Location_t(Pmax,v0,v1,t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - Location=[xt,yt]:t 时刻导弹的位置
% - Pmax
% - v0:指挥舰速度
% - v1:来袭导弹速度
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 计算导弹相对于指挥舰速度的 x 轴分量
vx=v1*cosd(220-180)+v0*sind(200-180); %237.2248% - 计算导弹相对于指挥舰速度的 y 轴分量
vy=v1*sind(220-180)+v0*cosd(200-180); %204.4276
% - 导弹相对运动方向与 x 轴夹角
A=atand(vy/vx);
% - 计算 xt
xt=vx*t-Pmax*cosd(A);
% - 计算 yt
yt=vy*t-Pmax*sind(A);
% - 整理输出
Location=[xt,yt];
(5)No_3_Attack_Or_Not.m 源代码
function attack_flag=No_3_Attack_Or_Not(Pmax,ship,v0,v1,v2,t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - attack_flag=[flag,det_t]
% - flag=1:表示可以发射防空导弹
% - det_t:拦截冻结时间
% - ship=[x,y,beta,l]
% - v0:指挥舰速度
% - v1:来袭导弹速度
% - v2:防空导弹速度
% - t:仿真时钟当前值
% 注:导弹发射准备时间为 7 秒
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%
% - 构建方程参数
a=v1^2-v2^2;
b=2*(v1^2)*(t+7)-2*cosd(ship(3))*v1*ship(4);
c= ship(4)^2 + ((t+7)^2)*(v1^2) - 2*cosd(ship(3))*v1*ship(4)*(t+7);
% - 构建方程
str=['(',num2str(a),')*x^2+(',num2str(b),')*x+(',num2str(c),')=0'];
% - 求解
x=solve(str);
x=double(x);
% - 分析结果
if x(1)<0det_t=x(2);
elseif x(2)<0det_t=x(1);elsedet_t=min([x(1),x(2)]);
end
% - 判断攻击条件
flag=1;
% - 条件 1:是否超出防空导弹射程
if det_t*v2>=80000flag=0;
end
if det_t*v2<=10000flag=0;
end
% - 条件 2:拦截地点距离指挥舰是否太近
attack_Location=No_3_Location_t(Pmax,v0,v1,t+det_t);
if sqrt(sum(attack_Location.^2))<10000 || t+det_t>605flag=0;
end
% - 整理输出
attack_flag=[flag,det_t];附录 4
(1)No_4_Example.mat 中数据
1.0e+003 *
0.8100 0.2810 0.2500 0.2020 0.0060 0.0030 0.0010
2.3000 0.2100 0.3000 0.3100 0.0040 0.0012 0.0020
0.8200 0.2800 0.2450 0.2010 0.0065 0.0054 0.0010
2.3250 0.2150 0.3200 0.3240 0.0042 0.0028 0.0020
0.8300 0.2820 0.2550 0.2000 0.0042 0.0047 0.0010
0.8250 0.2840 0.2500 0.2040 0.0050 0.0026 0.0010
2.2500 0.1500 0.3000 0.1550 0.0050 0.0033 0.0020
4.0000 0.1100 0.3000 0.0500 0.0034 0.0021 0.0030
2.8000 0.2600 0.2150 0.2600 0.0077 0.0068 0.0040
5.1200 0.1100 0.2100 0.0520 0.0036 0.0037 0.0050
4.0200 0.1200 0.2800 0.0520 0.0036 0.0017 0.0030
4.8000 0.1400 0.2200 0.0180 0.0096 0.0057 0.0050
0.4800 0.2950 0.2920 0.2450 0.0099 0.0069 0.0050
2.4500 0.2100 0.2300 0.2100 0.0050 0.0012 0.0050
2.9000 0.2900 0.2720 0.3500 0.0056 0.0052 0.0020
(2)No_4_Init.m 源代码
clc;
clear all;
% - 导入源数据(data 为 15x7 的矩阵,行为样本,列为属性)
load No_4_Example.mat;
total_std=std(No_4_Example(:,1:6),1);
new_std=total_std./sum(total_std);
new_std(2,:)=new_std(1,:);
new_std(3,:)=new_std(1,:);
new_std(4,:)=new_std(1,:);
new_std(5,:)=new_std(1,:);
% - 归一化
temp_he=sum(No_4_Example(:,1:6));
data(1:15,1)=No_4_Example(1:15,1)/temp_he(1);
data(1:15,2)=No_4_Example(1:15,2)/temp_he(2);
data(1:15,3)=No_4_Example(1:15,3)/temp_he(3);
data(1:15,4)=No_4_Example(1:15,4)/temp_he(4);
data(1:15,5)=No_4_Example(1:15,5)/temp_he(5);
data(1:15,6)=No_4_Example(1:15,6)/temp_he(6);
data(:,7)=No_4_Example(:,7);
% - 计算样本各个属性平均值和标准差% - u1 u2 u3 u4 u5 u6
% - v1
% - v2
% - v3
% - v4
% - v5
m=zeros(5,6); %平均值
n=zeros(5,6); %标准差
for i=1:5temp_data=zeros(1,6);temp_index=0;for j=1:15if data(j,7)==itemp_index=temp_index+1;temp_data(temp_index,1:6)=data(j,1:6);endendm(i,:)=mean(temp_data,1);if i==4n(i,:)=mean(temp_data);elsen(i,:)=std(temp_data,1);end
end
% - 导入待识别数据
Aim_data=[4021,213,142,61,7.0,3.5;
2830,206,269,13,9.2,5.7;
3622,221,230,10,4.6,1.9;
2032,220,195,307,5.2,4.3;
353,232,195,261,5.2,5.5;
1170,160,266,231,3.4,2.6;
1907,208,283,170,9.4,6.2;
4952,205,301,100,1.4,1.1;
6393,168,301,144,2.6,5.5;
6,163,301,174,2.6,5.5;
4738,236,177,99,6.0,1.7;
4748,235,177,358,6.0,1.7;
888,229,195,232,4.8,3.6;
877,227,195,114,4.8,3.6;
99,243,213,155,8.6,3.1;
92,241,213,278,8.6,3.1];
% - 归一化
temp_he=sum(Aim_data(:,1:6));
temp_Aim_data(1:length(Aim_data(:,1)),1)=Aim_data(1:length(Aim_data(:,1)),1)/temp_he(1);
temp_Aim_data(1:length(Aim_data(:,1)),2)=Aim_data(1:length(Aim_data(:,1)),2)/temp_he(2);
temp_Aim_data(1:length(Aim_data(:,1)),3)=Aim_data(1:length(Aim_data(:,1)),3)/temp_he(3);
temp_Aim_data(1:length(Aim_data(:,1)),4)=Aim_data(1:length(Aim_data(:,1)),4)/temp_he(4);
temp_Aim_data(1:length(Aim_data(:,1)),5)=Aim_data(1:length(Aim_data(:,1)),5)/temp_he(5);
temp_Aim_data(1:length(Aim_data(:,1)),6)=Aim_data(1:length(Aim_data(:,1)),6)/temp_he(6);
Aim_data=temp_Aim_data;
(3)No_4_Main.m 源代码
% - 程序初始化
No_4_Init;
tic;
% - 计算模糊评价矩阵
result=zeros(length(Aim_data(:,1)),1);
a=[1.8938,0.6209,0.0008,22.8997,2.8169];
for i=1:length(Aim_data(:,1))W=zeros(5,6);W(1,1:5)=No_4_Membership_1(a(1),Aim_data(i,:),m,n);W(2,1:5)=No_4_Membership_2(a(2),Aim_data(i,:),m,n);W(3,1:5)=No_4_Membership_3(a(3),Aim_data(i,:),m,n);W(4,1:5)=No_4_Membership_4(a(4),Aim_data(i,:),m,n);W(5,1:5)=No_4_Membership_5(a(5),Aim_data(i,:),m,n);W(1,6)=No_4_Judge_1(Aim_data(i,6),n(1,6));W(2,6)=No_4_Judge_2(Aim_data(i,6),n(2,6));W(3,6)=No_4_Judge_3(Aim_data(i,6),n(3,6));W(4,6)=No_4_Judge_4(Aim_data(i,6),n(4,6));W(5,6)=No_4_Judge_5(Aim_data(i,6),n(5,6));%W=sum(W')'/5;W=(sum((W.*new_std)'))';[value,index]=max(W);if index<1index=round(5*rand(1));endresult(i,1)=index;
end
result
toc
(4)No_4_Membership_1.m 源代码
function Membership_j=No_4_Membership_1(a,x,m,n)
%Membership_j=exp(-10*(x(1,1:5)-m(1,1:5)).^2./n(1,1:5).^2)*No_4_Judge_1(x(1,6),n(1,6));
Membership_j=exp(-a*(x(1,1:5)-m(1,1:5)).^2./n(1,1:5).^2);
(5)No_4_Membership_2.m 源代码
function Membership_j=No_4_Membership_2(a,x,m,n)
%Membership_j=exp(-10*(x(1,1:5)-m(2,1:5)).^2./n(2,1:5).^2)*No_4_Judge_2(x(1,6),n(2,6));
Membership_j=exp(-a*(x(1,1:5)-m(2,1:5)).^2./n(2,1:5).^2);
(6)No_4_Membership_3.m 源代码
function Membership_j=No_4_Membership_3(a,x,m,n)
%Membership_j=exp(-10*(x(1,1:5)-m(3,1:5)).^2./n(3,1:5).^2)*No_4_Judge_3(x(1,6),n(3,6));
Membership_j=exp(-a*(x(1,1:5)-m(3,1:5)).^2./n(3,1:5).^2);
(7)No_4_Membership_4.m 源代码
function Membership_j=No_4_Membership_4(a,x,m,n)
%Membership_j=exp(-10*(x(1,1:5)-m(4,1:5)).^2./n(4,1:5).^2)*No_4_Judge_4(x(1,6),m(4,6));
Membership_j=exp(-a*(x(1,1:5)-m(4,1:5)).^2./n(4,1:5).^2);
(8)No_4_Membership_5.m 源代码
function Membership_j=No_4_Membership_5(a,x,m,n)
%Membership_j=exp(-10*(x(1,1:5)-m(5,1:5)).^2./n(5,1:5).^2)*No_4_Judge_5(x(1,6),n(5,6));
Membership_j=exp(-a*(x(1,1:5)-m(5,1:5)).^2./n(5,1:5).^2);
(9)No_4_Judge_1.m 源代码
function y=No_4_Judge_1(x6,n_16)
if x6>=4%y=exp(-10*(x6-4)^2/n_16^2);y=0;
elsey=1;
end
(10)No_4_Judge_2.m 源代码
function y=No_4_Judge_2(x6,n_26)
y=1;
(11)No_4_Judge_3.m 源代码
function y=No_4_Judge_3(x6,n_36)
if x6>=4%y=exp(-10*(x6-4)^2/n_36^2);y=0;
elsey=1;
end
52
53
(12)No_4_Judge_4.m 源代码
function y=No_4_Judge_4(x6,n_46)
if x6<=2%y=exp(-10*(x6-2)^2/n_46^2);y=0;
elsey=1;
end
(13)No_4_Judge_5.m 源代码
function y=No_4_Judge_5(x6,n_56)
y=1;附录 5
(1)No_5_Init.m 源代码
clc;
clear all;
% - 设置仿真参数
t=0;
step=1;
flag=0;
r=10000;
b=10000;
Ts=0.1;
Us=0.1;
Tl=0.00001;
Ul=0.00001;
Ur=0.2;
Ub=0.1;
k=Ur/Ub;(2)No_5_Main.m 源代码
% - 程序初始化
No_5_Init;
% - 开始仿真
r_result=0;
b_result=0;
while flag==0if t>0r_result(t)=r;b_result(t)=b;temp_r=No_5_r(r,b,Us,k,Ub,Ul);temp_b=No_5_b(b,r,k,Ts,Ur,Tl);r=temp_r;b=temp_b;end% - 判断仿真是否终止if r<=0 || b<=0flag=1;elset=t+step;enddisp(['--> t= ',num2str(t),' , r= ',num2str(r),' , b= ',num2str(b)]);
endplot(1:t,r_result,1:t,b_result);(3)No_5_r.m 源代码
function y=No_5_r(r,b,Us,k,Ub,Ul)
y=r-Us*b*Ub/k-(1-Ub)*Ul*r*b/(k^2);
(4)No_5_b.m 源代码
function y=No_5_b(b,r,k,Ts,Ur,Tl)
y=b-k*Ts*r*Ur-(1-Ur)*Tl*(k^2)*r*b;