文章目录
- ● 300.最长递增子序列
- 思路
- 代码:
- ● 674. 最长连续递增序列
- 思路:
- 代码:
- ● 718. 最长重复子数组
- 思路:
- 代码一:dp二维数组
- 代码二:滚动数组
● 300.最长递增子序列

思路
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度


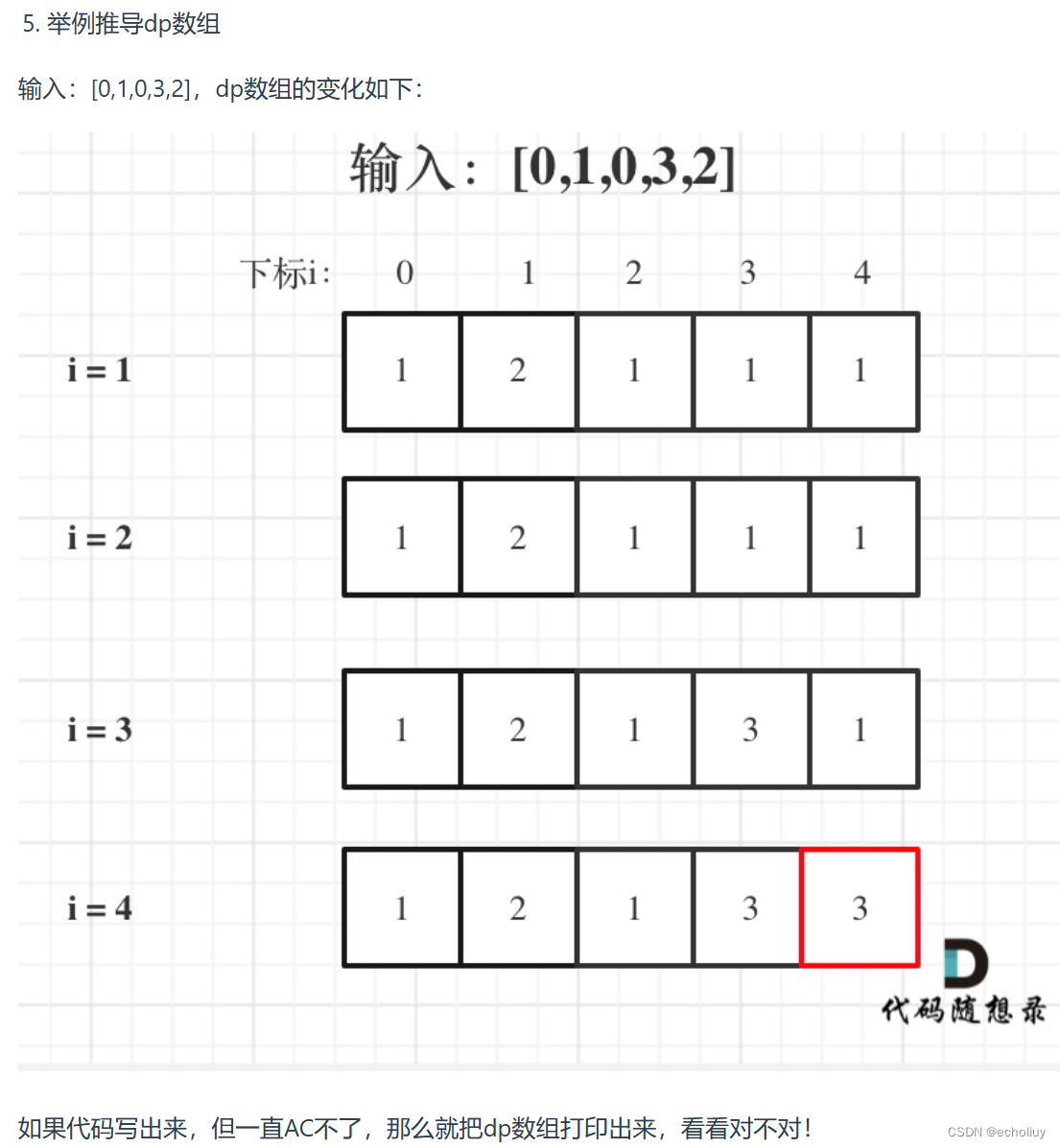
代码:
注意:需要判断[0]输出是1的情况。
class Solution {public int lengthOfLIS(int[] nums) {// if(nums.length==1)return 1;int[] dp = new int[nums.length];int res = 1;Arrays.fill(dp, 1);for(int i=1;i<nums.length;i++){for(int j=0;j<i;j++){if(nums[j]<nums[i]){dp[i]=Math.max(dp[i],dp[j]+1);}}res = Math.max(res, dp[i]);}return res;}
}● 674. 最长连续递增序列

思路:

代码:
class Solution {public int findLengthOfLCIS(int[] nums) {int[] dp=new int[nums.length];Arrays.fill(dp,1);int res=1;for(int i=1;i<nums.length;i++){if(nums[i]>nums[i-1]){dp[i]=dp[i-1]+1;}res=Math.max(res,dp[i]);}return res;}
}
● 718. 最长重复子数组

思路:


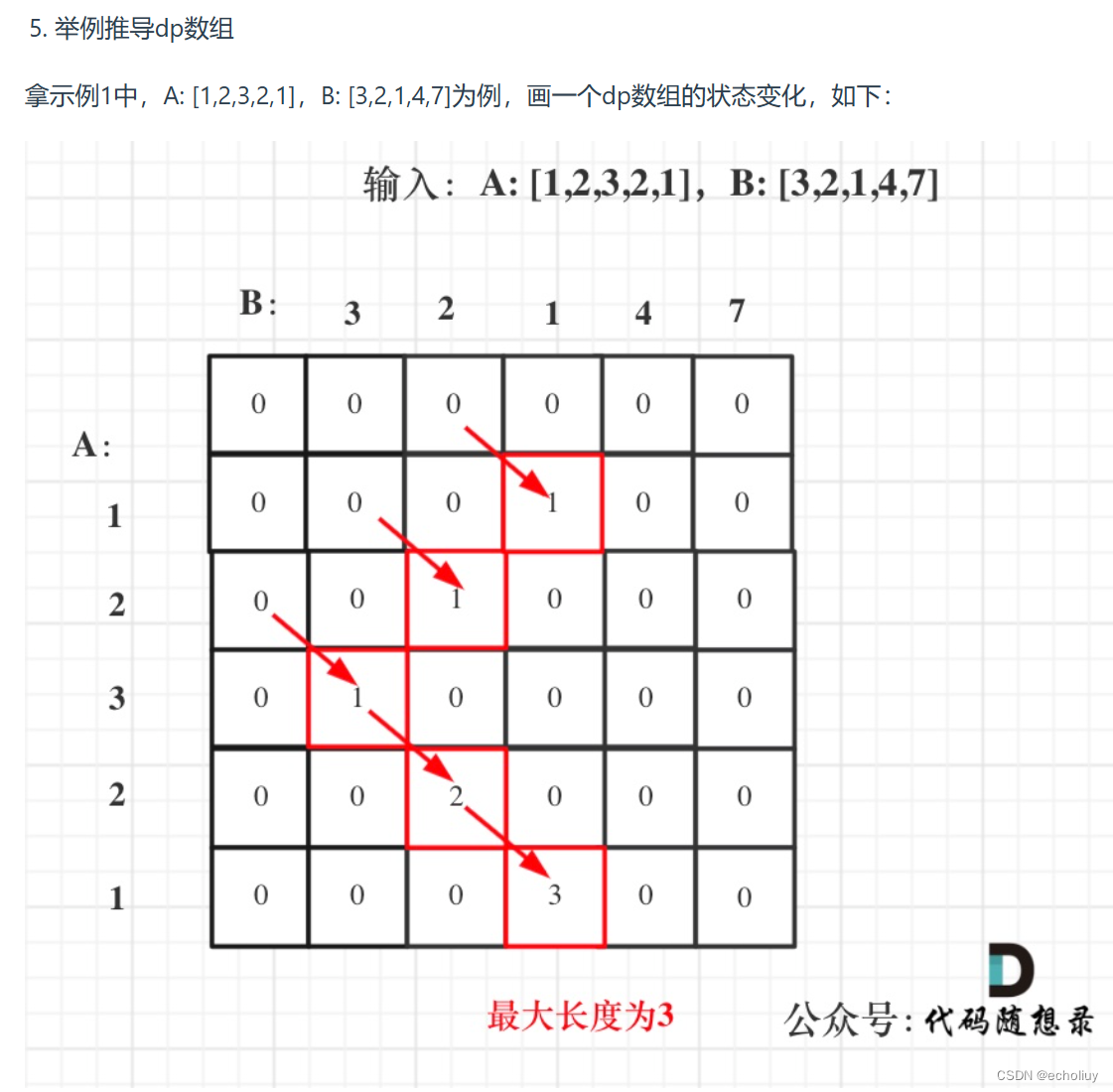
代码一:dp二维数组
class Solution {public int findLength(int[] nums1, int[] nums2) {int res = 0;int[][] dp = new int[nums1.length + 1][nums2.length + 1];for(int i=1;i<=nums1.length;i++){//循环是为了匹配for(int j=1;j<=nums2.length;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}res = Math.max(res,dp[i][j]);}}return res;}
}
代码二:滚动数组
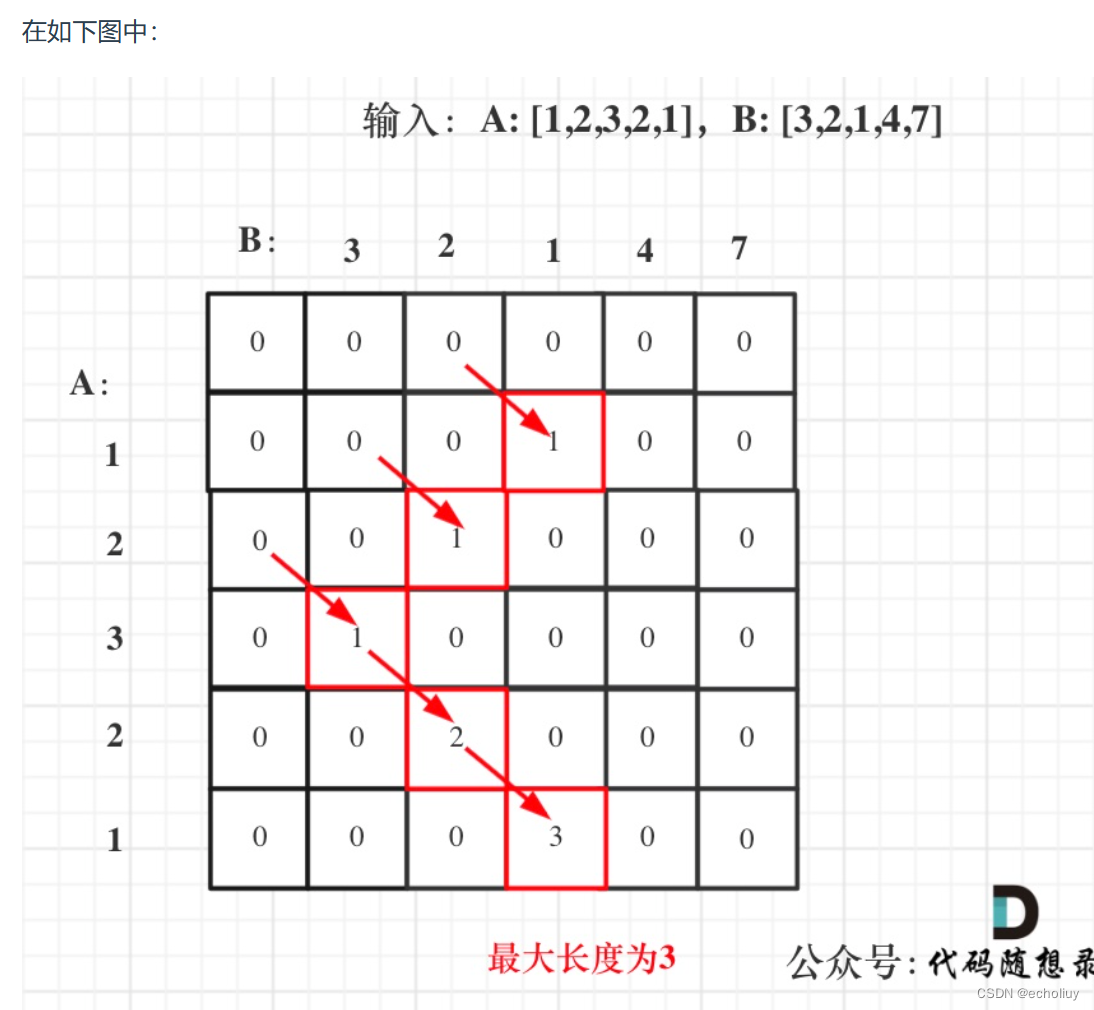
我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组,也就是dp[j]都是由dp[j - 1]推出。
也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。
此时遍历B数组的时候,就要从后向前遍历,这样避免重复覆盖。
// 版本二
class Solution {public int findLength(int[] nums1, int[] nums2) {int res = 0;int[]dp = new int[nums2.length + 1];for(int i=1;i<=nums1.length;i++){//循环是为了匹配for(int j=nums2.length;j>0;j--){if(nums1[i-1]==nums2[j-1]){dp[j]=dp[j-1]+1;}else{dp[j]=0;}res = Math.max(res,dp[j]);}}return res;}
}