一、第一题:壁画
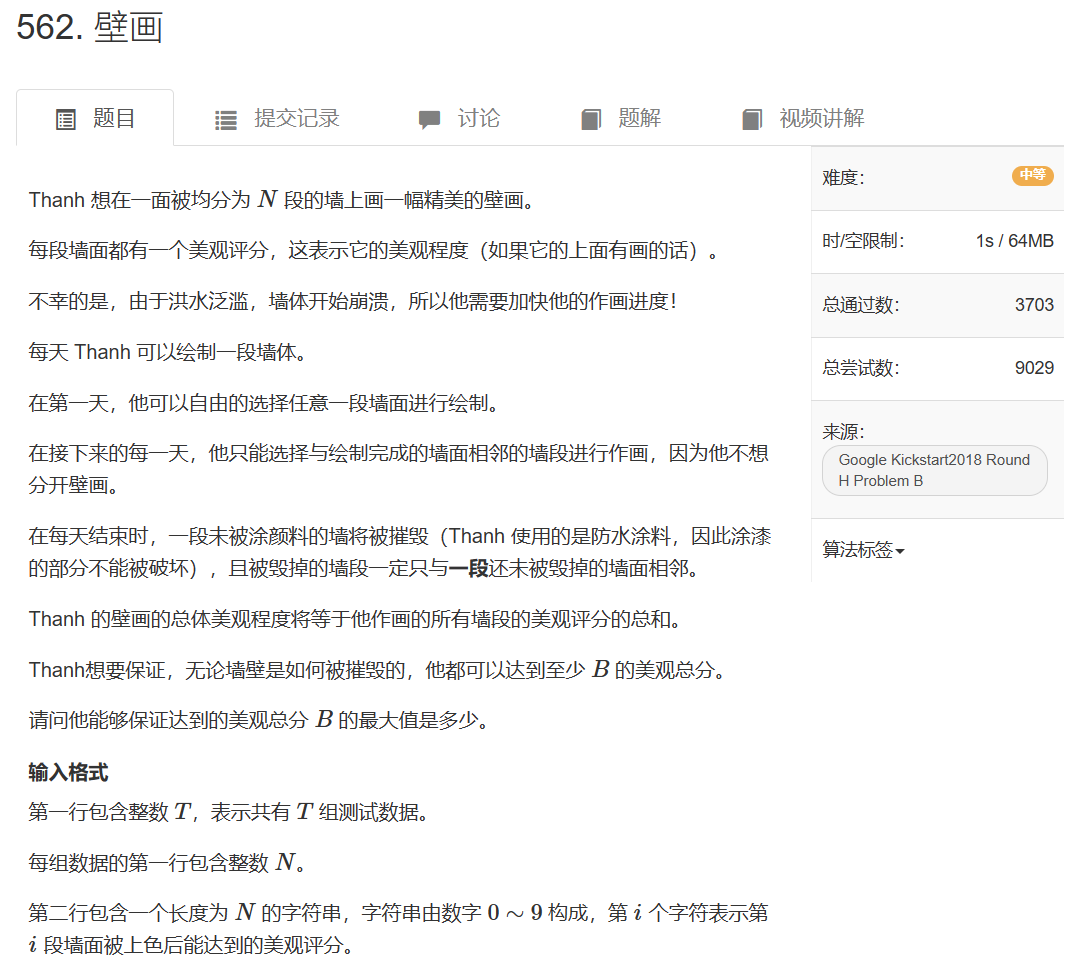
 解题思路:前缀和+贪心枚举
解题思路:前缀和+贪心枚举
仔细思考可以发现B值最大的情况是一段连续的长度为n/2上取整的序列的累加和
【Python程序代码】
import math
T = int(input())
for _ in range(1,1+T):n = int(input())s = input()l = math.ceil(len(s)/2)a = [0]for i in s:a.append(int(i))for i in range(1,n+1):a[i]+=a[i-1]res = 0for i in range(l,n+1):res = max(res,a[i]-a[i-l])print("Case #%d: %d"%(_,res))二、第二题:前缀和


解题思路:前缀和
前缀和模板题
【Python程序代码】
n,m = map(int,input().split())
a = [0] + list(map(int,input().split()))
for i in range(1,n+1):a[i]+=a[i-1]
for i in range(m):l,r = map(int,input().split())print(a[r]-a[l-1])三、第三题:子矩阵的和


解题思路:二维前缀和
二维前缀和模板题
【Python程序代码】
n, m, q = map(int, input().split())
a = [[0] * (m + 1)]
for i in range(n):tep = [0] + list(map(int, input().split()))a.append(tep)
s = [[0] * (m + 5) for _ in range(n + 5)]
for i in range(1, n + 1):for j in range(1, m + 1):a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]
for _ in range(q):x1, y1, x2, y2 = map(int, input().split())res = a[x2][y2] - a[x1 - 1][y2] - a[x2][y1 - 1] + a[x1 - 1][y1 - 1]print(res)
四、第四题: K倍区间

解题思路:前缀和
先计算数组的前缀和并对k取模后思考如何组成k倍区间
【Python程序代码】
from collections import defaultdict
dic = defaultdict(int)
n,k = map(int,input().split())
a = [0]
for i in range(n):tep = int(input())a.append(tep)
for i in range(1,n+1):a[i] = (a[i]+a[i-1])%k
res = 0
#print(a)
for i in range(0,n+1):res += dic[a[i]]dic[a[i]] += 1
print(res)
五、第五题:统计子矩阵
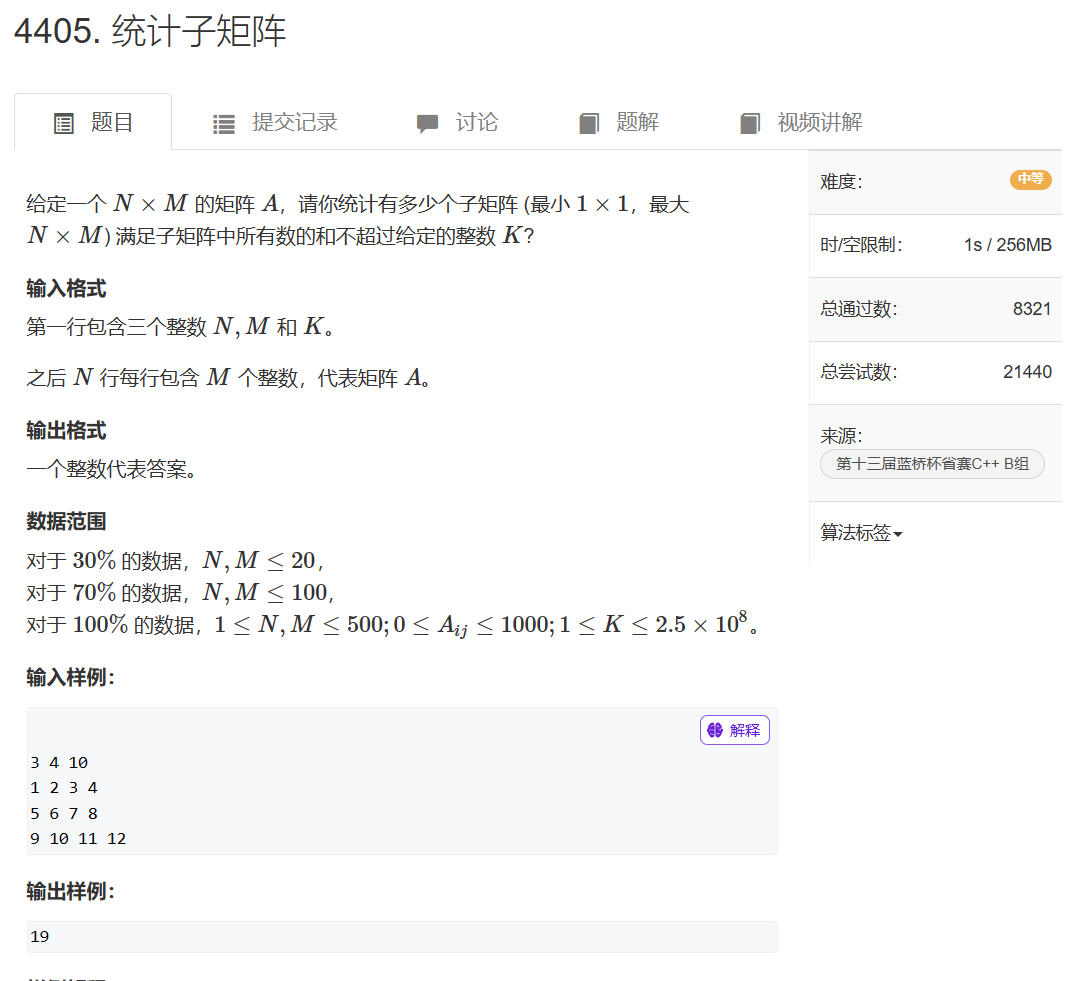
解题思路:前缀和+双指针优化
首先对列做前缀和方便后面的优化,从第一行(i)开始遍历,y方向则是(i~n),左指针l每次从1开始,右指针遍历1~m,每次判断(l,r,y)组成的子矩阵,如果当前的值大于k则左指针往右走直到小于k,否则res+=r-l+1.
【Python程序代码】
n,m,k = map(int,input().split())
s = [[0]*(m+1)]
for i in range(n):s.append([0] + list(map(int,input().split())))
for i in range(1,n+1):for j in range(1,m+1):s[i][j] += s[i-1][j]
res = 0
for i in range(1,n+1):for j in range(i,n+1):l = 1sumv = 0for r in range(1,m+1):sumv += s[j][r]-s[i-1][r]while sumv>k:sumv -= s[j][l]-s[i-1][l]l += 1res += r-l+1
print(res)