动态规划课堂4-----子数组系列

引入：

例题1：最大子数组和

例题2：环形子数组的最大和

例题3：乘积最大子数组

例题4：乘积为正数的最长子数组

总结：

结语：

引入：

在动态规划（DP）子数组系列中，我们还是用前面几节所用的解题思路1. 状态表示，2.状态转移方程，3.初始化，4.填表顺序，5.返回值。在写代码时一定要把这5步考虑清楚再写代码。写代码时其步骤也比较固定分别为：1.创建 dp 表 2.初始化 3.填表 4.返回值。写代码时可以按照这4步骤写不会乱也不会把哪一部分漏掉😎。

在子数组系列问题最常用到的状态表示是：以i位置元素为结尾的所有子数组的........(题目要求).

这个非常重要，后面的题基本都是用这个模板的状态表示。

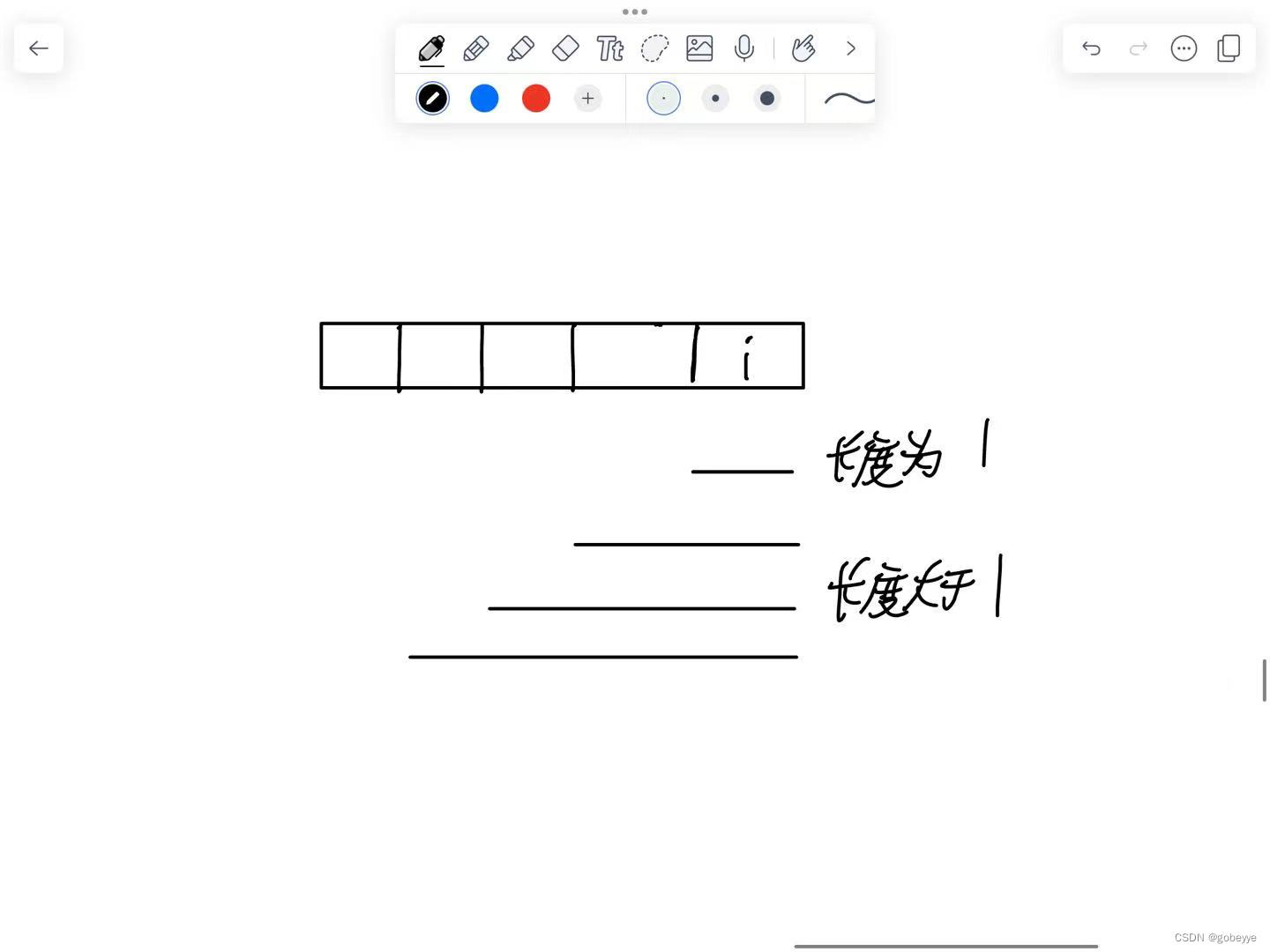
例如下图：可以将其分为两种情况长度为1和长度大于1两种情况，剩下的分析要见具体题目。

例题1：最大子数组和

链接：最大子数组和

题目简介：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组：

是数组中的一个连续部分。

解法（动态规划）：

1. 状态表示：

dp[i] 表示：以i 位置元素为结尾的「所有⼦数组」中和的最⼤和。设个状态表示会贯穿我们这一整个系列。

2.状态转移方程

dp[i] 的所有可能可以分为以下两种：

（1）子数组的⻓度为1 ：此时dp[i] = nums[i] ；（就只有它本身）

（2）子数组的⻓度⼤于1 ：此时dp[i] 应该等于以i - 1 做结尾的「所有⼦数组」中和的最⼤值再加上nums[i] ，也就是dp[i - 1] + nums[i] 。

由于我们要的是「最⼤值」，因此应该是两种情况下的最⼤值，因此可得转移⽅程： dp[i] = max(nums[i], dp[i - 1] + nums[i]) 。

3.初始化：

辅助结点法：

注意点：（1）辅助结点⾥⾯的值要保证后续填表是正确的.（2）下标的映射关系.

在本题中，最前⾯加上⼀个格⼦，并且让dp[0] = 0 即可。之所以设为0是因为根据1.状态表示，0位置没有元素（因为dp表加了一个辅助节点故dp表的0下标对应数组的-1下标），而我们的dp里面的值是最大和，没有数组故其和为0.

4.填表顺序：

从左往右

5.返回值：

状态表示为以i 为结尾的所有⼦数组的最⼤值，但是最⼤⼦数组和的结尾我们是不确定的（可能前面很大最后一个数非常小导致其不是最大值）。因此我们需要返回整个dp 表中的最大值。

代码实现如下：

class Solution {public int maxSubArray(int[] nums) {//1.创建 dp 表//2.初始化//3.填表//4.返回值int n = nums.length;int[] dp = new int[n + 1];for(int i = 1;i <= n;i++){dp[i] = Math.max(nums[i - 1],dp[i - 1] + nums[i - 1]);}int max = dp[1];for(int i = 1;i <= n;i++){//加上辅助节点后要注意下标的映射关系，还有循环的边界。max = Math.max(max,dp[i]);}return max;}
}

时间复杂度：O（n）

空间复杂度：O（n）

例题2：环形子数组的最大和

链接：环形子数组的最大和

题目简介：

给定一个长度为 n 的环形整数数组 nums ，返回 nums 的非空 子数组 的最大可能和 。

环形数组 意味着数组的末端将会与开头相连呈环状。形式上， nums[i] 的下一个元素是 nums[(i + 1) % n] ， nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。

子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上，对于子数组 nums[i], nums[i + 1], ..., nums[j] ，不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。

解法（动态规划）：

我们可以将最大和子数组大致划分为下面两个部分，一个是正常在中间的，另一个在头尾两边的。

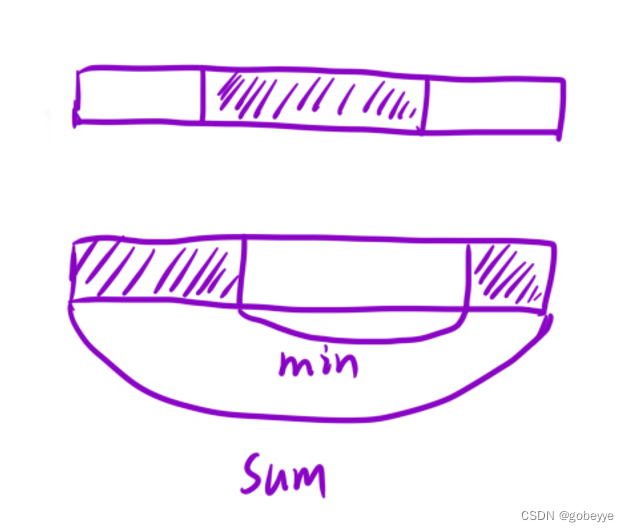
这一题是例题1的升级版，如果有友友分析过的话会发现直接进行规划非常困难，那么我们能不能采用另一种思维。既然整个数组的和sum是不变的那么要求头尾两边的子数组我们能不能求正常中间数组的最小值将sum减去这个最小值不就是我们头尾两边的子数组的最大值。

1. 状态表示：

f[i] 表⽰：以i 做结尾的「所有⼦数组」中和的最大值。

g[i] 表⽰：以i 做结尾的「所有⼦数组」中和的最小值。

2.状态转移方程：

由于f[i]在上一题已经分析过故这里只分析g[i].

（1）子数组的⻓度为1 ：此时g[i] = nums[i] ；

（2）子数组的⻓度⼤于1 ：此时g[i] 应该等于以i - 1 做结尾的所有⼦数组中和的最⼩值再加上nums[i] ，也就是g[i - 1] + nums[i] 。

由于我们要的是最小子数组和，因此应该是两种情况下的最⼩值，因此可得转移⽅程：g[i] = min(nums[i], g[i - 1] + nums[i]) 。

3.初始化：

辅助节点法.

前面加上⼀个格子，并且让g[0] = 0，f[0] = 0,根据状态表示为0，没有元素那么和显然为0.

4.填表顺序：

从左往右

5.返回值：

按正常情况来我们应该返回f（）里面的最大值，和g表里面的最小值-sum，但是有一种特殊的情况如下图，就是如果数组的数全为负数的情况下，g表会把所有的负数都加入，然后sum-g表就会等于0，下面的正确最大和为-1（sum-g表最小值等于0的情况就相当于一个子数组里面一个数都没有这是题目不允许的）

故我们返回sum == gmin ? fmax : max(fmax, sum - gmin)。这样就可以排除全为负数的情况。

代码实现如下：

class Solution {public int maxSubarraySumCircular(int[] nums) {//1.创建 dp 表//2.初始化//3.填表//4.返回值int n = nums.length;int sum = 0;for(int i = 0;i < n;i++){sum += nums[i];}int[] f = new int[n + 1];int[] g = new int[n + 1];for(int i = 1;i <= n;i++){f[i] = Math.max(nums[i - 1],nums[i - 1] + f[i - 1]);g[i] = Math.min(nums[i - 1],nums[i - 1] + g[i - 1]);}int max1 = f[1];for(int i = 1;i <= n;i++){max1 = Math.max(max1,f[i]);}int max2 = -0x3f3f3f3f;for(int i = 1;i <= n;i++){if(sum == g[i]){max2 = Math.max(max2,-0x3f3f3f3f);}else{max2 = Math.max(sum - g[i],max2);}}return Math.max(max1,max2);}
}

max2初始化为-0x3f3f3f3f是因为求最大值初始化的值要够小，之所以不初始化为Integer.MIN_VALUE,这是因为这个数如果再发生减法的话可能会变成无穷大，0x3f3f3f3f这个数够小且稳定。

时间复杂度：O（n）

空间复杂度：O（n）

例题3：乘积最大子数组

链接：乘积最大子数组

题目简介：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

解法（动态规划）：

这题乍一看好像和最大子数组和好像差不多，但是乘法要考虑正负号的因素，如果只有一个dp表存储表示乘积最大子数组那么下面这种情况的最大值只能是5，可是结果是30.所以只有一个dp表是不够的，我们还需要一个表来存储最小值（乘于一个负数就变成最大值）。

1. 状态表示：

f[i] 表⽰：以i 结尾的所有⼦数组的最大乘积。

g[i] 表⽰：以i 结尾的所有⼦数组的最小乘积。

2.状态转移方程：

对于f[i] ，也就是「以i 为结尾的所有⼦数组的最⼤乘积」，对于所有⼦数组，可以分为下面三种形式：

（1）子数组的⻓度为1 ，也就是nums[i]。

（2）子数组的⻓度⼤于1 ，但nums[i] > 0 ，此时需要的是i - 1 为结尾的所有⼦数组的最⼤乘积f[i - 1] ，再乘上nums[i] ，也就是nums[i] * f[i - 1] 。

（3）子数组的⻓度⼤于1 ，但nums[i] < 0 ，此时需要的是i - 1 为结尾的所有⼦数组的最⼩乘积g[i - 1] ，再乘上nums[i] ，也就是nums[i] * g[i - 1] 。

如果nums[i] = 0 ，所有⼦数组的乘积均为0 ，三种情况其实都包含了。

综上所述， f[i] = max(nums[i], max(nums[i] * f[i - 1], nums[i] * g[i - 1]) )。

对于g[i] ，也就是「以i 为结尾的所有子数组的最⼩乘积」，对于所有⼦数组，可以分为下面三种形式：

（1）子数组的⻓度为1 ，也就是nums[i] 。

（2）子数组的⻓度⼤于1 ，但nums[i] > 0 ，此时需要的是i - 1 为结尾的所有⼦数组的最⼩乘积g[i - 1] ，再乘上nums[i] ，也就是nums[i] * g[i - 1] 。

（3）子数组的⻓度⼤于1 ，但nums[i] < 0 ，此时需要的是i - 1 为结尾的所有⼦数组的最⼤乘积f[i - 1] ，再乘上nums[i] ，也就是nums[i] * f[i - 1] 。

综上所述， g[i] = min(nums[i], min(nums[i] * f[i - 1], nums[i] * g[i - 1])) 。

3.初始化：

辅助节点：

f[0] = g[0] = 1。

4.填表顺序：

从左往右，两个表⼀起填。

5.返回值：

返回f 表中的最⼤值

代码如下：

class Solution {public int maxProduct(int[] nums) {//1.创建 dp 表//2.初始化//3.填表//4.返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];g[0] = f[0] = 1;for(int i = 1;i <= n;i++){f[i] = nums[i - 1];g[i] = nums[i - 1];if(nums[i - 1] >= 0){f[i] = Math.max(f[i],nums[i - 1] * f[i - 1]);g[i] = Math.min(nums[i - 1] * g[i - 1],g[i]);}else{f[i] = Math.max(f[i],nums[i - 1] * g[i - 1]);g[i] = Math.min(g[i],nums[i - 1] * f[i - 1]);}}int max = f[1];for(int i = 1;i <= n;i++){max = Math.max(max,f[i]);}return max;}
}

时间复杂度：O（n）

空间复杂度：O（n）

例题4：乘积为正数的最长子数组

链接：乘积为正数的最长子数组

题目简介：

解法（动态规划）：

但是，如果我们知道「以i - 1 为结尾的所有子数组，乘积为负数的最长子数组的⻓度」neg[i - 1] ，那么此时的dp[i] 是不是就等于neg[i - 1] + 1呢？

通过上⾯的分析，我们可以得出，需要两个dp 表，才能推导出最终的结果。不仅需要⼀个乘积为正数的最长子数组，还需要⼀个乘积为负数的最长子数组。

1. 状态表示：

f[i] 表⽰：以i 结尾的所有⼦数组中，乘积为正数的最长子数组的⻓度。

g[i] 表⽰：以i 结尾的所有⼦数组中，乘积为负数的最长子数组的⻓度。

2.状态转移方程：

推状态转移方程时最好画图来帮助我们理解。

对于f[i] ，也就是以i 为结尾的乘积为正数的最⻓⼦数组，根据nums[i] 的值，可以分为三种情况：

（1）nums[i] = 0 时，所有以i 为结尾的⼦数组的乘积都不可能是正数，此时f[i] = 0 .

（2）nums[i] > 0 时，那么直接找到f[i - 1] 的值（这⾥请再读⼀遍f[i - 1] 代表的意义，并且考虑如果f[i - 1] 的结值是0的话，影不影响结果），然后加⼀即可，此时f[i] = f[i - 1] + 1.

（3）nums[i] < 0 时，此时我们要看g[i - 1] 的值（这⾥请再读⼀遍g[i - 1] 代表的意义。因为负负得正，如果我们知道以i - 1 为结尾的乘积为负数的最⻓⼦数组的⻓度，加上1即可），根据g[i - 1] 的值，⼜要分两种情况：

1.g[i - 1] = 0 ，说明以i - 1 为结尾的乘积为负数的最长子数组是不存在的，⼜因为nums[i] < 0，所以以i 结尾的乘积为正数的最长子数组也是不存在的，此时f[i] = 0。

2.g[i - 1] != 0 ，说明以i - 1 为结尾的乘积为负数的最长子数组是存在的，⼜因为nums[i] < 0 ，所以以i 结尾的乘积为正数的最长子数组就等于g[i - 1] + 1。

综上所述， nums[i] < 0 时， f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;

3.初始化：

辅助节点法：

f[0] = g[0] = 0。

4.填表顺序：

从左往右，两个表⼀起填。

5.返回值：

根据状态表⽰，我们要返回f 表中的最⼤值。

代码如下：

class Solution {public int getMaxLen(int[] nums) {//1.创建 dp 表//2.初始化//3.填表//4.返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];for(int i = 1;i <= n;i++){if(nums[i - 1] > 0){f[i] = f[i - 1] + 1;g[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;}else if(nums[i - 1] < 0){f[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}else{f[i] = 0;g[i] = 0;}}int max = f[1];for(int i = 1;i <= n;i++){max = Math.max(max,f[i]);}return max;}
}

时间复杂度：O（n）

空间复杂度：O（n）