深度学习_卷积

卷积

卷积（Convolution）是数学和计算机科学中的一个重要概念，特别在信号处理和图像处理中应用广泛。在信号处理领域，卷积是两个函数之间的一种数学操作，它表示两个函数的重叠部分的积分量。

在图像处理中，卷积通常用于图像滤波和特征提取。卷积操作通过将一个函数（通常是一个图像）与另一个函数（通常是一个小的滤波器或内核）进行卷积运算来生成一个新的函数（通常是一个处理后的图像）。这个滤波器或内核在输入图像上滑动，并与输入图像的局部区域进行卷积操作，从而对图像进行平滑、边缘检测、特征增强等处理。

卷积在深度学习和神经网络中也起到了重要作用。在卷积神经网络（Convolutional Neural Networks，CNNs）中，卷积层使用可学习的卷积核来提取图像的特征，从而实现图像分类、目标检测等任务。通过在网络中堆叠多个卷积层，可以逐渐提取出更加抽象和高级的特征，使网络能够对输入的图像进行更加复杂的分析和理解。

卷积在pytorch中有两种实现方式：

torch.nn.Conv2d()
torch.nn.functional.conv2d()

输入要求：
torch.autograd.Variable()的类型：
大小是(batch, channel, H, W)
batch------一批数据的数量
channel------输入的通道数（彩色3，灰度1，卷积网络中通道数可达几十到几百个）
H------图像的高度
W------图像的宽度

实例

图像准备：
将图像放在代码相同文件夹中
在这里插入图片描述

加载图像并显示

python库准备：

numpy
torch
matplotlib

代码：

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
im = Image.open('./cat.png').convert('L')  # 打开图像文件，并将图像转换为灰度图
im = np.array(im, dtype='float32')  # 将图像转换为numpy数组，数据类型是32位浮点数
# plt.imshow(im.astype('uint8'), cmap='gray')  # 显示，转换为无符号8位整型
# plt.show()  # 让图像窗口保持打开状态

执行代码得到小猫灰度图：
在这里插入图片描述

定义卷积算子进行轮廓检测：

-用 torch.nn.Conv2d()对图像进行操作：

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
im = Image.open('./cat.png').convert('L')  # 打开图像文件，并将图像转换为灰度图
im = np.array(im, dtype='float32')  # 将图像转换为numpy数组，数据类型是32位浮点数
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
# 将numpy数组转换为pytorch张量，并将其形状调整为(1,1,im.shape[0], im.shape[1])即卷积层期望输入具有四个维度：(batch_size, channels, height, width)
conv1 = nn.Conv2d(1, 1, 3, bias=False)
# 输入通道数1表示灰度图像，输出通道数1表示生成的特征图的数量。卷积核大小为 3，表示一个 3x3 的卷积核。bias=False 表示在卷积中不使用偏置项。
sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32')
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3))  # Sobel边缘检测卷积核，并将其形状调整为(1, 1, 3, 3)
conv1.weight.data = torch.from_numpy(sobel_kernel)
edge1 = conv1(Variable(im))  # 张量 im 传递给卷积层，得到了输出张量 edge1
edge1 = edge1.data.squeeze().numpy()  # 张量中提取NumPy数组，并使用.squeeze()去除维度为1的尺寸
plt.imshow(edge1, cmap='gray')
plt.show()

结果：
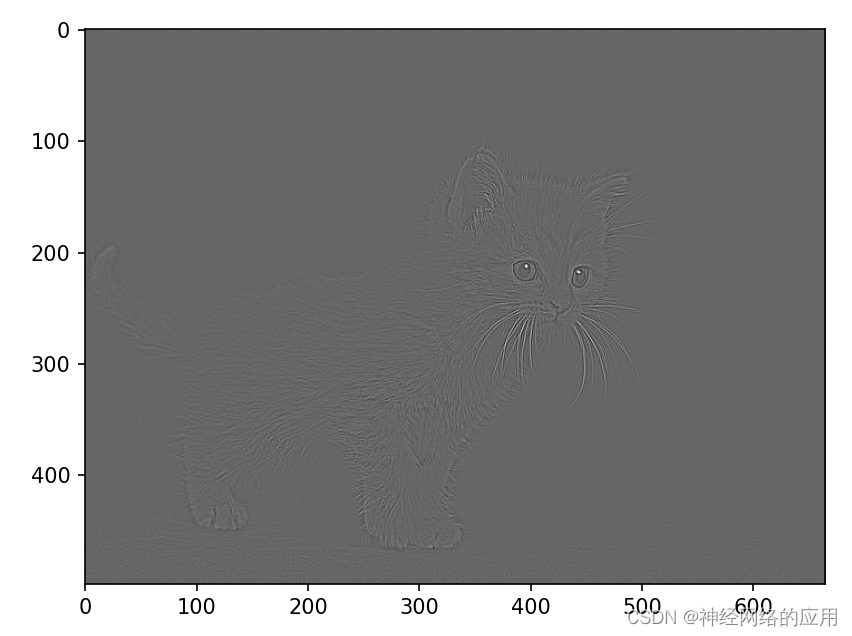
在这里插入图片描述

用 torch.nn.functional.conv2d() 对图像进行操作：

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
im = Image.open('./cat.png').convert('L')  # 打开图像文件，并将图像转换为灰度图
im = np.array(im, dtype='float32')  # 将图像转换为numpy数组，数据类型是32位浮点数
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32')
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3))
weight = Variable(torch.from_numpy(sobel_kernel))
edge2 = F.conv2d(Variable(im), weight)
edge2 = edge2.data.squeeze().numpy()
plt.imshow(edge2, cmap='gray')
plt.show()

结果图：
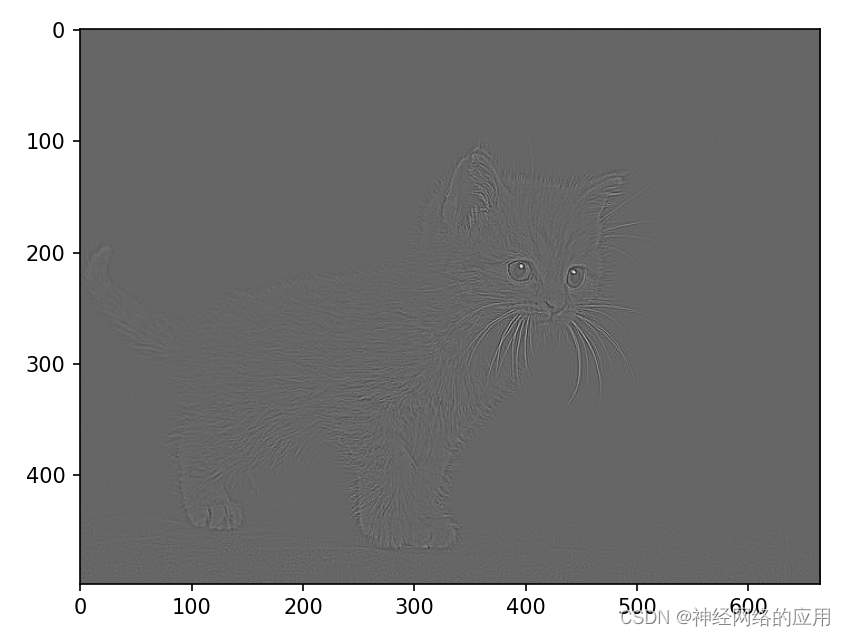
在这里插入图片描述

可以看到上面两种方法所得结果相同，那么区别是什么呢？

分析

在PyTorch中，torch.nn.Conv2d()和torch.nn.functional.conv2d()都是用于进行二维卷积操作的函数，区别在于：

模块（Module）与函数（Function）：
- torch.nn.Conv2d()是一个模块（Module），属于PyTorch的神经网络模块之一。这意味着它是一个具有状态的对象，可以在神经网络中被实例化、调用，并且具有可学习的参数。
- torch.nn.functional.conv2d()是一个函数（Function），属于PyTorch的函数式接口。这意味着它是一个纯函数，不包含任何可学习的参数，通常在用户需要更大的灵活性时使用。
使用方式：
- torch.nn.Conv2d()通常与其他模块一起使用，例如在构建神经网络时作为网络的一部分。它被实例化为一个对象，可以通过调用该对象进行卷积操作，并且包含了可学习的卷积核参数。
- torch.nn.functional.conv2d()通常在用户需要在神经网络的前向传播中进行卷积操作时使用。由于它是一个函数，可以直接调用该函数进行卷积操作，但需要手动传递卷积核参数。
参数传递：
- 在使用torch.nn.Conv2d()时，通常需要将输入数据和卷积核参数传递给该对象的实例，并且可以通过调用实例进行卷积操作。
- 在使用torch.nn.functional.conv2d()时，需要手动传递输入数据、卷积核参数以及其他参数，如步幅（stride）、填充（padding）等。