多模匹配算法之AC算法详解
算法概述
Aho-Corasick算法
- 这是一种字典匹配算法,它用于在输入文本中查找字典中的字符串。时间复杂度是线性的。该算法应用有限自动机巧妙地将字符比较转化为了状态转移。
该算法的基本思想
− 在预处理阶段,AC自动机算法建立了三个函数,转向函数goto,失效函数failure和输出函数output,由此构造了一个树型有限自动机。
− 在搜索查找阶段,则通过这三个函数的交叉使用扫描文本,定位出关键字在文本中的所有出现位置。
字典树的构造
- 要匹配的一些字符串添加到树结构中去,树边就是单词中的字符,单词中最后一个字符的连接节点添加标志,以表示改节点路径包含1个字典中的字符串,搜索到此节点就表示找到了字典中的某个单词,可以直接输出。
例:模式串集合 P={he,she,his,hers},下面的分析都根据这个集合展开
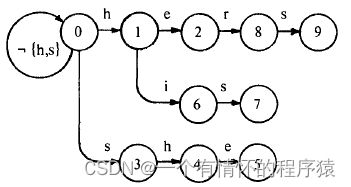
图1
转向函数goto原理
我们规定g(state1,ch) = state2.:状态state1 经过 字符ch 可以到达状态state2 。(1)模式串he:g(0,h)=1 g(1,e)=2 模式串he的转向函数构造完毕;
(2)模式串she:g(0,s)=3 g(3,h)=4 g(4,e)=5 模式串she构造完毕;
(3)模式串his:g(0,h)=1 g(1,i)=6 g(6,s)=7 模式串hers构造完毕;
(4)模式串hers:g(0,h)=1 g(1,e)=2 g(2,r)=8 g(8,s)=9 模式串hers构造完毕;
注:(3)中g(0,h)为何不跳到6状态,原因(这个跳转也已存在,所以无需在添加新的状态),(4)中的g(0,h)=1 g(1,e)=2一样的原因。
整个模式串集合构造完毕。可以根据转向函数画出上面的图1。
输出函数output原理
在转向函数构造的基础上实现输出函数output()。模式串he最后的状态为状态2。当模式匹配的时候遇到状态2。说明待匹配的字符串,已经匹配到了模式串he。在构造模式串的转向函数的结尾,来完成output函数的构建。
失效函数failure原理
在转向函数的基础上实现失效函数f()。规定:深度为1的状态失效跳转到状态0,即f(1)=0,f(3)=0;(因为第一个字符匹配都失败了,所以只能从新开始匹配)
当前字符无匹配,表示当前状态的任何一条路径都无法达到下一跳,此时不能沿现有路径前进,只能回溯,回溯到存在的最长的后缀字符串处,如果没有任何后缀字符串匹配则回溯到树根处。然后从当前回溯节点判断是否可以到达目标字符串字符。
失效函数理解有些难。算法的实现却很巧妙。
失效函数算法:
规定:f(1) = 0 f(3) = 0 ; (第一个字符匹配都失败了,所以只能从新开始匹配)
g(1,e) = 2; f(2) = g(f(1),e) = g(0,e) = 0;
g(1,i) = 6; f(6) = g(f(1),i) = g(0,i) = 0;
g(3,h) = 4; f(4) = g(f(3),h) = g(0,h) = 1;
g(2,r) = 8; f(8) = g(f(2),r) = g(0,2) = 0;
g(6,s) = 7; f(7) = g(f(6),s) = g(0,s) = 3;
g(4,e) = 5; f(5) = g(f(4),e) = g(1,e) = 2;
g(8,s) = 9; f(9) = g(f(8),s) = g(0,s) = 3;
注:此图所构造的失效函数跳转没有遇到失败的情况,有可能会出现失效的情况,具体培训的时候会讲到。(f(N) = g(f(M),s) | g(f(f(M)),s)......如果前面任意的一个跳转不为-1,就赋值给f(N)).
所有的失效跳转构造完毕 ,可以得到:
state 1 2 3 4 5 6 7 8 9
f 0 0 0 1 2 0 3 0 3
算法实现的失效状态的先后顺序:1,3,2,6,4,8,7,5,9
通过队列的方式来实现:首先深度为1的状态入队列1和3入队列,然后1出队列的同时它的下一跳2和6入队列。然后3出队列的同时它的下一跳4入队列,下一步2出队列它的下一跳8入队列;下一步6出队列它的下一跳7入队列;直到9出队列,队列为空,失效函数构建完毕。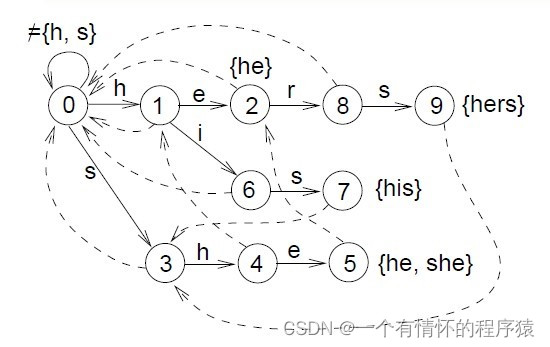
算法使用的存储结构
1.AC字典树的存储结构
typedef struct
{
int acsmMaxStates; /*总的模式串的长度*/
int acsmNumStates; /*状态,实现跳转函数g*/
ACSM_PATTERN * acsmPatterns; /*模式串链表头*/
ACSM_STATETABLE * acsmStateTable; /*状态链表,g*/
}ACSM_STRUCT;
/*ACSM_STRUCT * acsm*/
/*acsm->acsmStateTable[M].NextState[i] = N; 意思就是g(M,i) = N;*/
2. 模式串存储结构
typedef struct _acsm_pattern
{
struct _acsm_pattern *next;
unsigned char *patrn; /*经过转化以后的模式串*/
unsigned char *casepatrn; /*源模式串*/
int n; /*源模式串长度*/
int nocase; /*模式串是否进行大小写转化*/
void *id; /*保留字段,未用*/
int nmatch; /*该模式串所匹配的次数*/
} ACSM_PATTERN;
3.状态表
typedef struct
{
int NextState[ ALPHABET_SIZE ]; /*下一跳*/
int FailState; /*失效函数f的跳转*/
ACSM_PATTERN *MatchList; /*输出函数的存储链表头*/
}ACSM_STATETABLE;
转向函数goto的实现
转向函数g(状态,字符) = 下一个状态的构建。
例:模式串集合(he,she,his,hers)
第一个模式串he,g(0,h)=1, g(1,e)=2;
第二个模式串she,g(0,s)=3, g(3,h)=4,g(4,e)=5;
第三个模式串his, g(0,h) =1,g(1,i)=6,g(6,s)=7;
第四个模式串hers, g(0,h) =1, g(1,e)=2,g(2,r)=8,g(8,s)=9.
*如果字符匹配到了状态2,5,7,9就说明了已经匹配上了关键字。构建输出函数output。
static void AddPatternStates (ACSM_STRUCT * acsm, ACSM_PATTERN * p)
{
unsigned char *pattern;
int state=0, next, n;
n = p->n;
pattern = p->patrn;