【Godot4.2】基于SurfaceTool的3D网格生成与体素网格探索

概述

说明：本文基础内容写于2023年6月，由三五篇文章汇总而成，因为当时写的比较潦草，过去时间也比较久了，我自己都得重新阅读和理解一番，才能知道自己说了什么，才有可能重新优化整理。

因为我对体素网格的原始算法并不精通，当时只是依靠自己的直觉以及Godot4.2提供的工具类来实现了自己的一套Godot体素网格生成算法。

你也可以把本文当做这些工具类的实例教程进来看。因此体素不体素的你也可以当我没说：），重点在于在Godot中用代码进行3D网格的生成。

体素的性能问题

如果直接使用立方体网格堆叠的方式，则会存在很多不显示但是真实存在的面，立方体一多，就会加重GPU进行各种矩阵变换、投影计算的负担，从而导致卡顿。

因此，好的体素网格生成算法，一定首先是要做到面数优化，最好是看不见的面一个都不生成。这样才能在地图尺寸比较大，存在数以万计的体素时，能够做到最少的顶点数量，从而最大程度减少GPU运算和渲染的负担，减少卡顿情况的出现。

在Godot中程序化生成3D网格

Godot提供了一个叫SurfaceTool的类（当然还有其他的类），可以用十分底层（定义顶点、法线、UV）的方式创建3D网格资源，这就让程序化生成3D网格有了可能，并有了动态融并网格的算法可能。

与2D中使用多个点自定义、多边形、折线等几何图形一样，3D中也是用三维空间中的多个点来定义三维网格（Mesh）。

不同点是，三维网格，是由三角面构成的，也就是由3个顶点构成一个三角面，多个三角面构成一个三维网格。

SurfaceTool的应用

搭建SurfaceTool简单测试场景

通过创建一个含有MeshInstance3D的简单3D场景+一个简单的EditorScript脚本，就可以搭建一个基础的SurfaceTool测试场景。

框架代码如下：

@tool
extends EditorScriptfunc _run():var ins:MeshInstance3D = get_scene().get_node("MeshInstance3D")ins.mesh = create_mesh()passfunc create_mesh():var st = SurfaceTool.new()# ...return mesh

其中自定义函数create_mesh()用于SurfaceTool实例的创建和3D网格的返回。
_run()则在运行后，对场景中的MeshInstance3D节点的mesh属性赋值。

这样做的好处是，可以直接在编辑器中看到网格的样子。
比如下面的代码：

@tool
extends EditorScriptfunc _run():var ins:MeshInstance3D = get_scene().get_node("MeshInstance3D")ins.mesh = create_mesh()passfunc create_mesh():var st = SurfaceTool.new()st.begin(Mesh.PRIMITIVE_TRIANGLES)# Prepare attributes for set_vertex.st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(0, 0))# Call last for each vertex, adds the above attributes.st.add_vertex(Vector3(-1, -1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(0, 1))st.add_vertex(Vector3(-1, 1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(1, 1))st.add_vertex(Vector3(1, 1, 0))# Commit to a mesh.var mesh = st.commit()return mesh

运行后，生成了如下的3D网格：

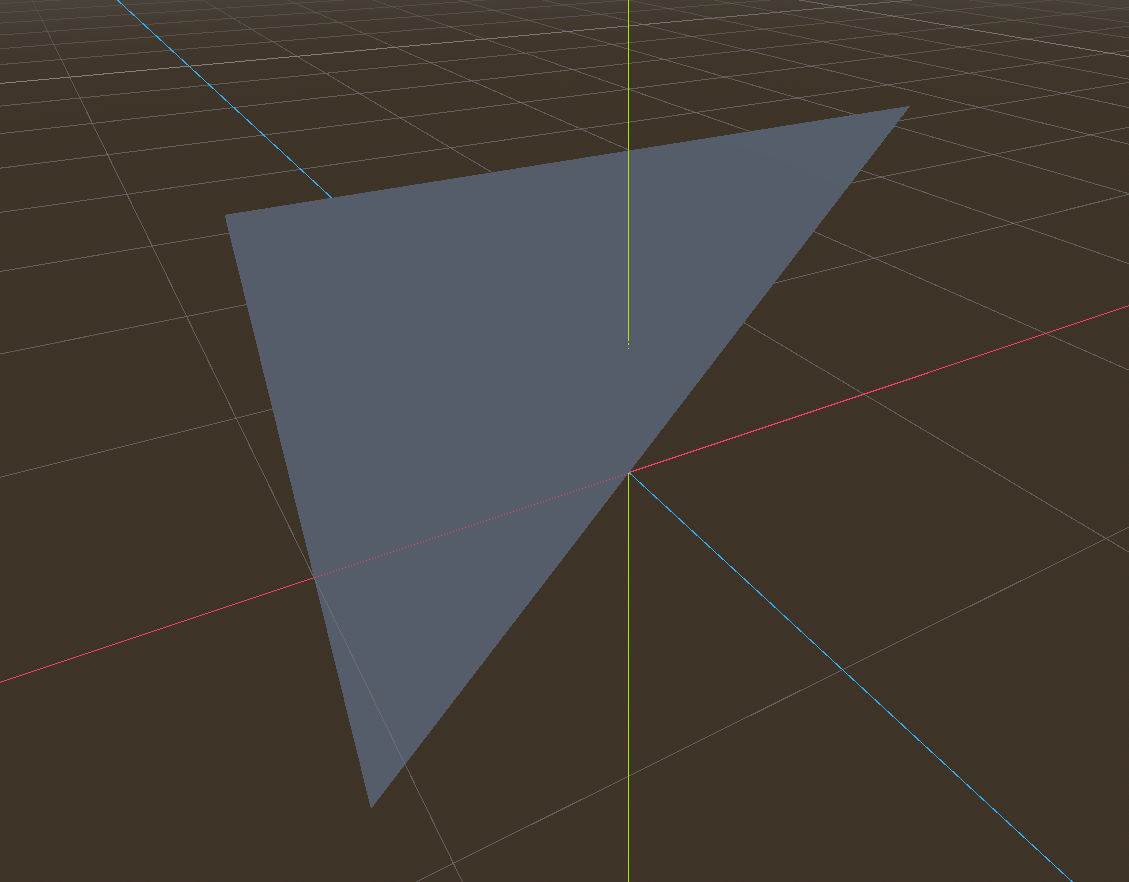
在后视图可以看到其实际的形状是一个等腰直角三角形的三角面。

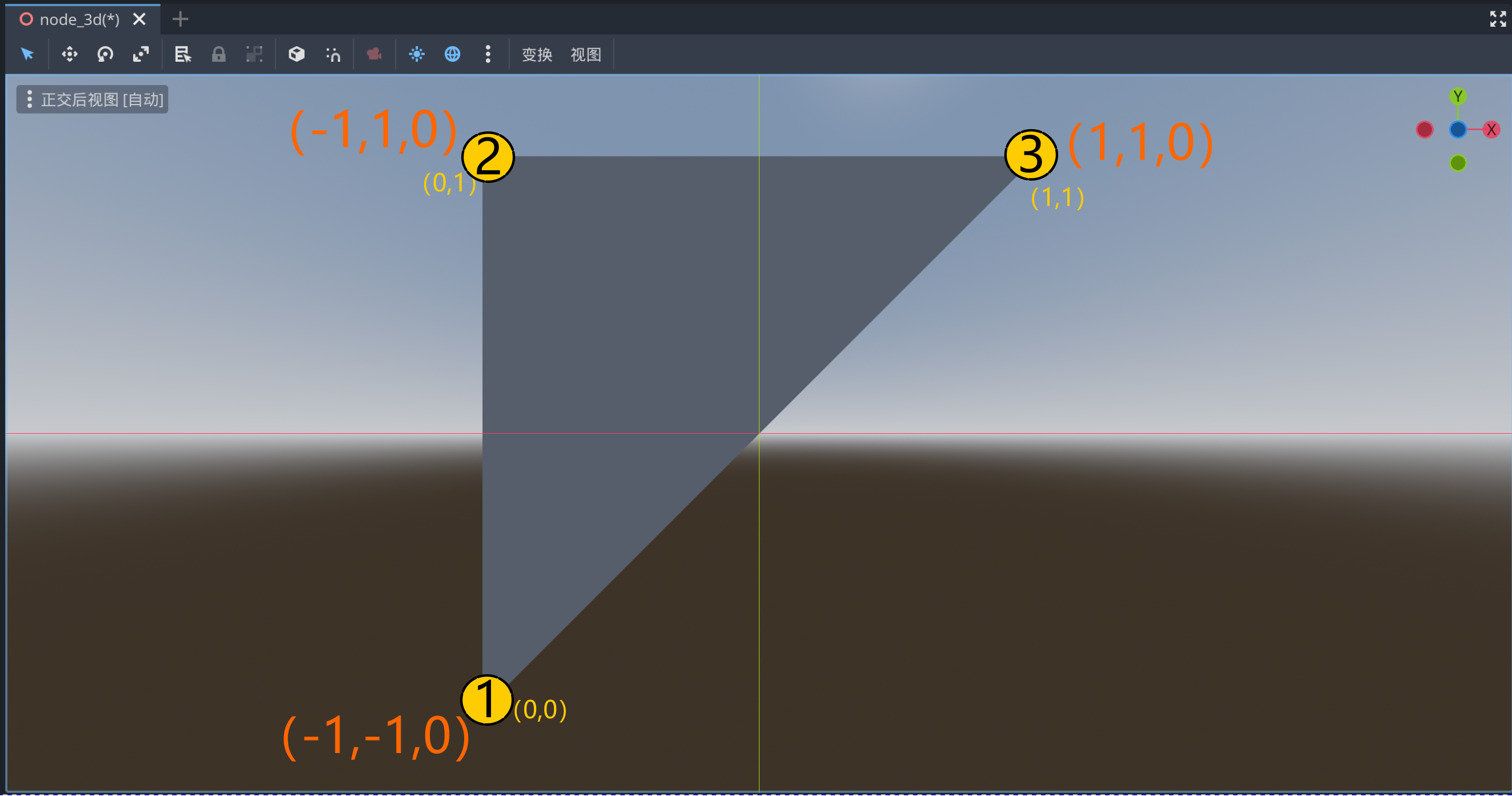
法线都是（0,0,1）。而且UV坐标在垂直方向是反的。

生成方形网格

会生成三角面了，那么生成方形网格也就不难了，方形网格可以看做是两个三角面组成。
执行如下脚本：

@tool
extends EditorScriptfunc _run():var ins:MeshInstance3D = get_scene().get_node("MeshInstance3D")ins.mesh = create_mesh()passfunc create_mesh():var st = SurfaceTool.new()st.begin(Mesh.PRIMITIVE_TRIANGLES)st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(0, 0))st.add_vertex(Vector3(-1, -1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(0, 1))st.add_vertex(Vector3(-1, 1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(1, 1))st.add_vertex(Vector3(1, 1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(1, 1))st.add_vertex(Vector3(1, 1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(1, 0))st.add_vertex(Vector3(1, -1, 0))st.set_normal(Vector3(0, 0, 1))st.set_uv(Vector2(0, 0))st.add_vertex(Vector3(-1, -1, 0))# Commit to a mesh.var mesh = st.commit()return mesh

生成的方形网格如下：
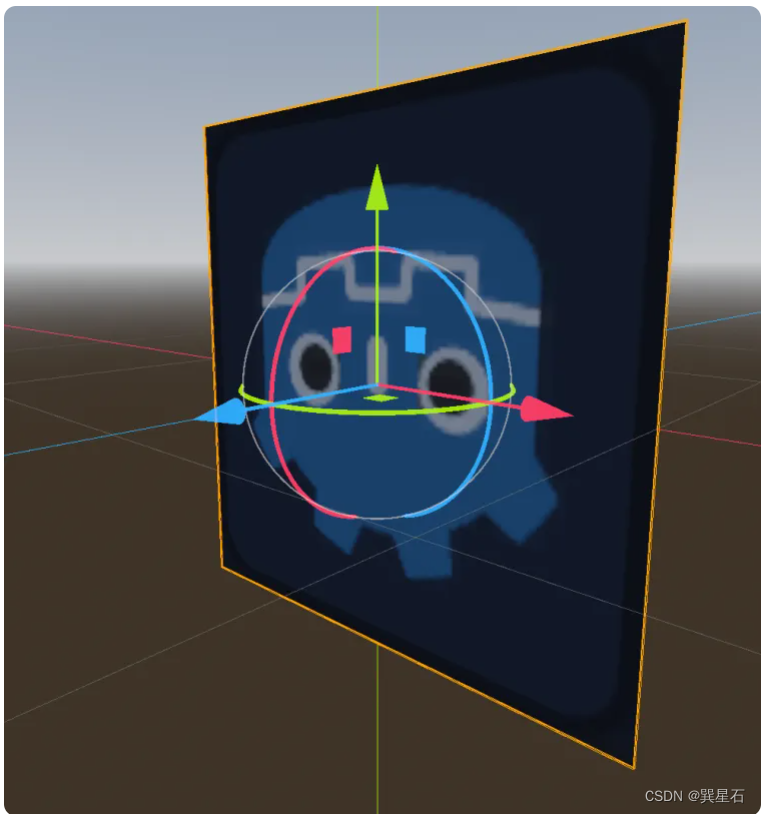
在这里插入图片描述
其顶点和UV以及三角面的示意图如下：

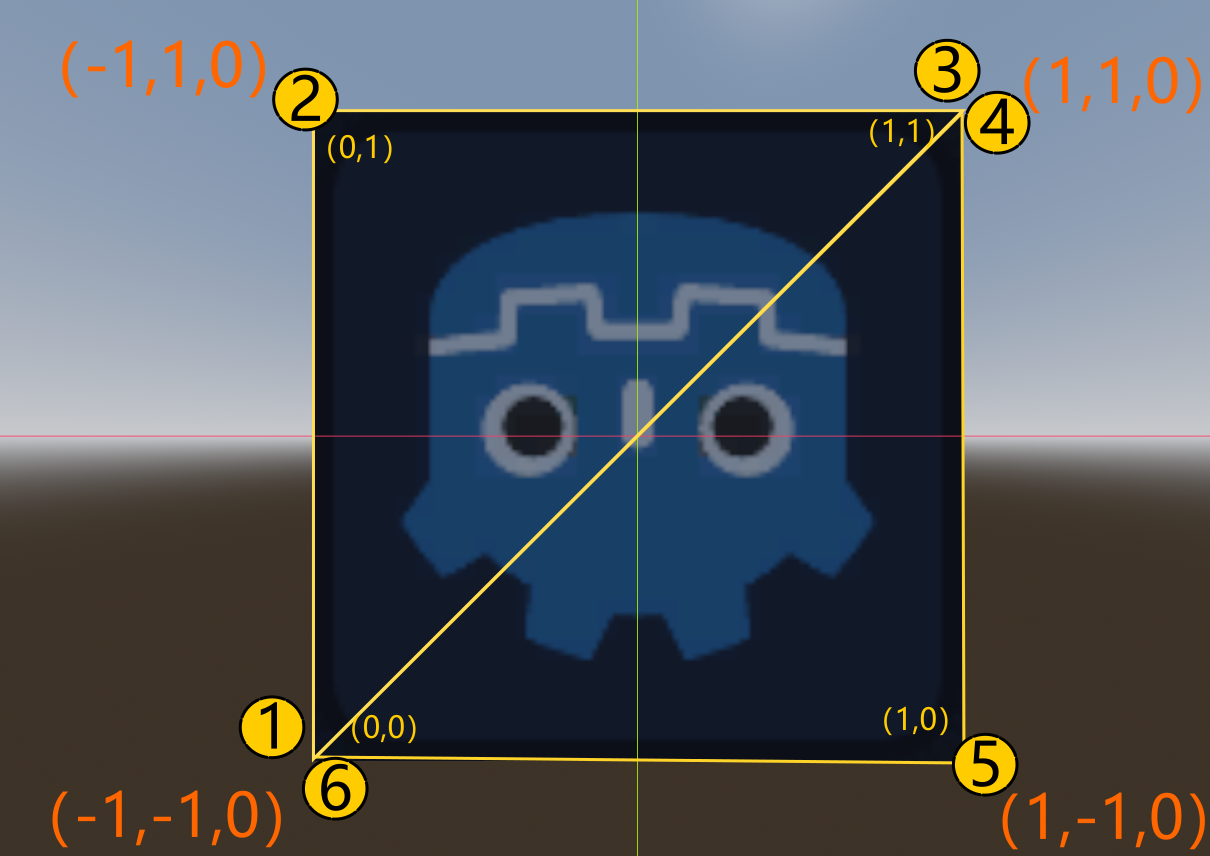
注意：

添加顶点的顺序非常重要，如果不按首尾顺序添加，则法线可能相反。
每3个点组成一个三角面，如果顶点不够，就会报错。

创建立方体

在Godot中，可以使用一个AABB来表示一个基本的立方体。
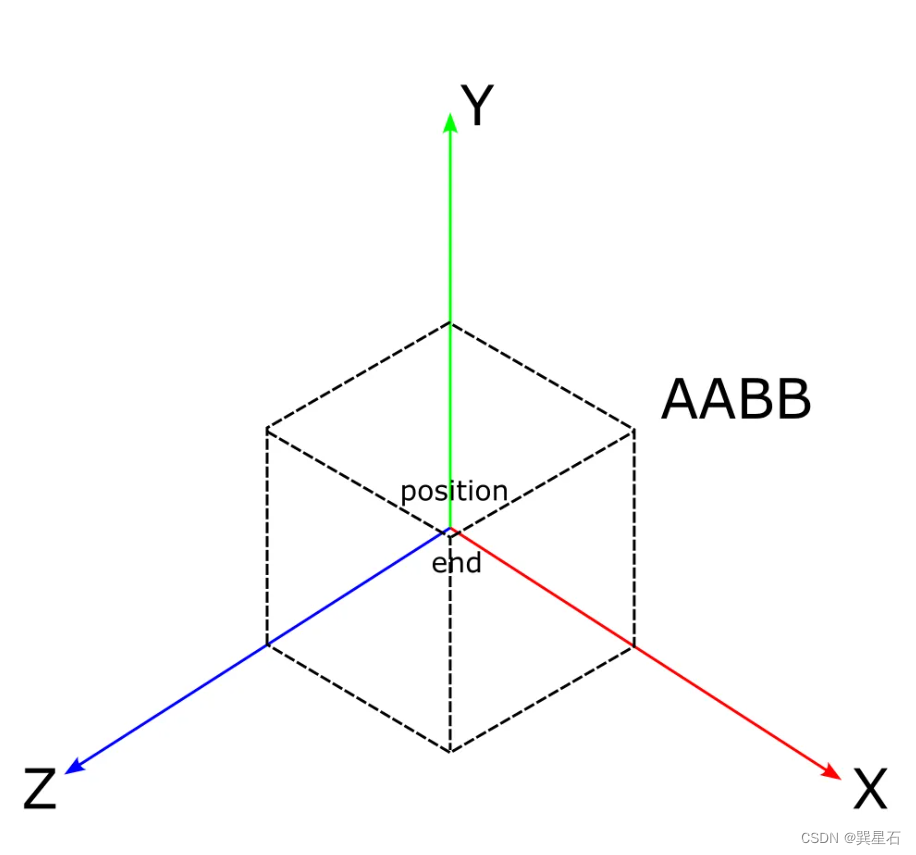
在这里插入图片描述

通过简单的三维向量加减法运算，就可以获得AABB代表的立方体的所有顶点坐标。

而通过立方体的顶点坐标，就可以求出组成六个面各自的两个三角面。

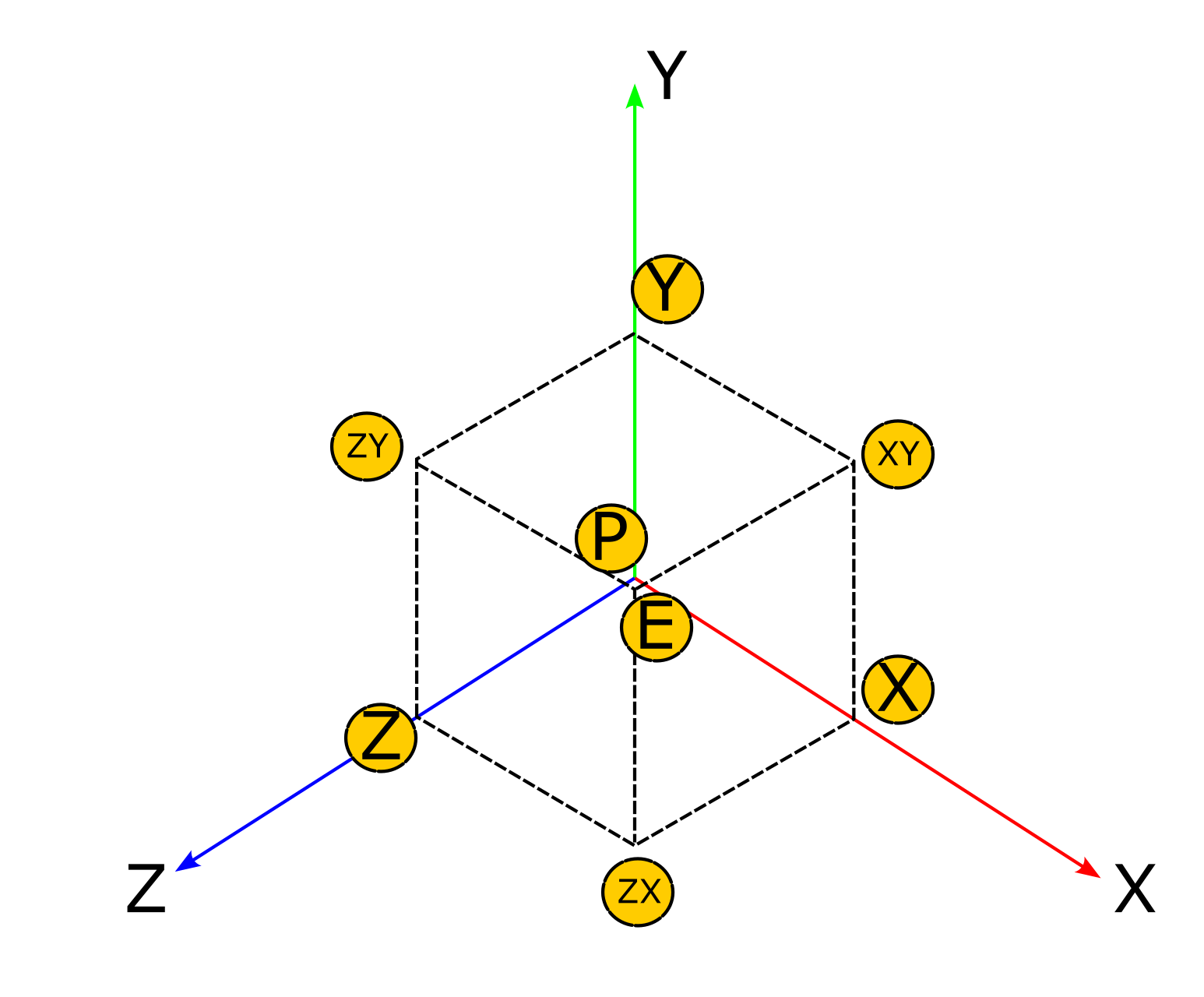
# 三条坐标轴方向的边的端点
var p_Z = (0,0,end.z) # Z轴
var p_Y = (0,end.y,0) # Y轴
var p_X = (end.x,0,0) # X轴
# 三个平面上的点的端点
var p_YZ = (0,end.y,end.z) # YZ平面
var p_XZ = (end.x,0,end.z) # XZ平面
var p_XY = (end.x,end.y,0) # XY平面

上面的点坐标是基于一个position=Vector3.ZERO，然后size = Vector3.ONE的AABB进行计算的。
其他位置的立方体可以通过AABB的变换得到。
如果想要获得以坐标原点为中心的矩形，可以设置position=-Vector3.ONE/2，然后size = Vector3.ONE的AABB。并将上述所有的0变成postion相应轴上的分量。也就是：

# 三条坐标轴方向的边的端点
var p_Z = (position.x,position.y,end.z) # Z轴
var p_Y = (position.x,end.y,position.z) # Y轴
var p_X = (end.x,position.y,position.z) # X轴
# 三个平面上的点的端点
var p_YZ = (position.x,end.y,end.z) # YZ平面
var p_XZ = (end.x,position.y,end.z) # XZ平面
var p_XY = (end.x,end.y,position.z) # XY平面

定义6个面的法线和顶点顺序

为六个面定义名称：

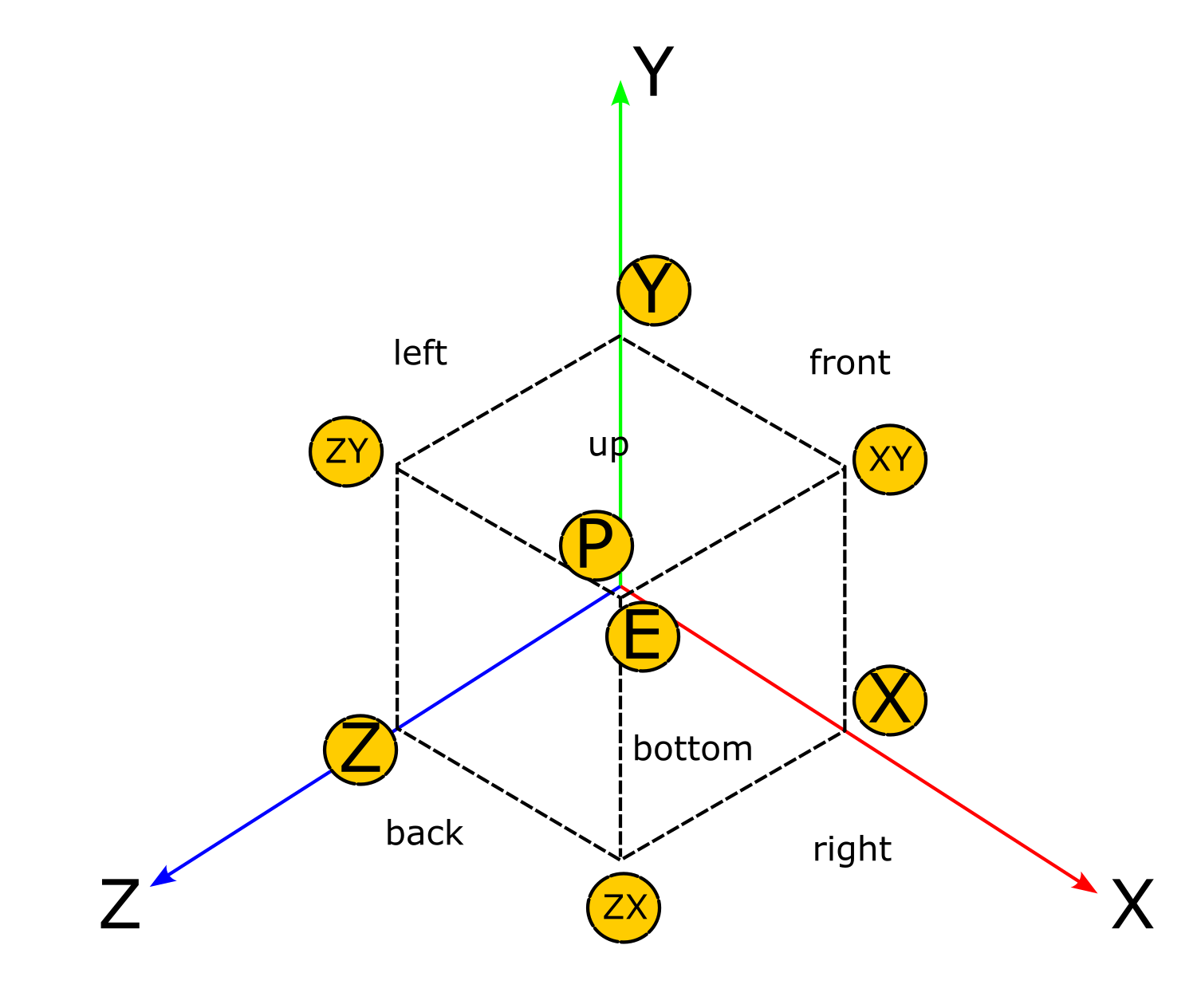
# UV坐标
var uvs = [Vector2.DOWN,Vector2.ZERO,Vector2.RIGHT,Vector2.ONE]
# 右侧面
var f_right = {normal = Vector3.RIGHT,vectors = [p_XZ,p_E,p_XY,p_XY,p_X,p_XZ]
}

实现后的完整代码如下：

@tool
extends EditorScriptfunc _run():var ins:MeshInstance3D = get_scene().get_node("MeshInstance3D")ins.mesh = create_cubemesh()func create_cubemesh():var st = SurfaceTool.new()st.begin(Mesh.PRIMITIVE_TRIANGLES)# 构造AABBvar position = Vector3.ZEROvar size = Vector3.ONEvar box:AABB = AABB(position,size)var end = box.end# ============= 获得立方体8个顶点的坐标# positon和andvar p_P = positionvar p_E = end# 三条坐标轴方向的边的端点var p_Z = Vector3(position.x,position.y,end.z) # Z轴var p_Y = Vector3(position.x,end.y,position.z) # Y轴var p_X = Vector3(end.x,position.y,position.z) # X轴# 三个平面上的点的端点var p_YZ = Vector3(position.x,end.y,end.z) # YZ平面var p_XZ = Vector3(end.x,position.y,end.z) # XZ平面var p_XY = Vector3(end.x,end.y,position.z) # XY平面# 6个顶点的UV坐标顺序var uvs = [Vector2.DOWN,Vector2.ZERO,Vector2.RIGHT,Vector2.ONE]# ============= 定义立方体6个面的法线和顶点绘制顺序# 右侧面var faces = {f_right = { # 右侧面normal = Vector3.RIGHT,vectors = [p_XZ,p_E,p_XY,p_X]},f_up = { # 上面normal = Vector3.UP,vectors = [p_E,p_YZ,p_Y,p_XY]},f_left = { # 左侧面normal = Vector3.LEFT,vectors = [p_P,p_Y,p_YZ,p_Z]},f_bottom = { # 底面normal = Vector3.DOWN,vectors = [p_Z,p_XZ,p_X,p_P]},f_front = { # 前面normal = Vector3.FORWARD,vectors = [p_X,p_XY,p_Y,p_P]},f_bcak = { # 后面normal = Vector3.BACK,vectors = [p_Z,p_YZ,p_E,p_XZ]}}for face in faces:for i in [0,1,2,2,3,0]:st.set_normal(faces[face]["normal"])st.set_uv(uvs[i])st.add_vertex(faces[face]["vectors"][i])var mesh = st.commit()return mesh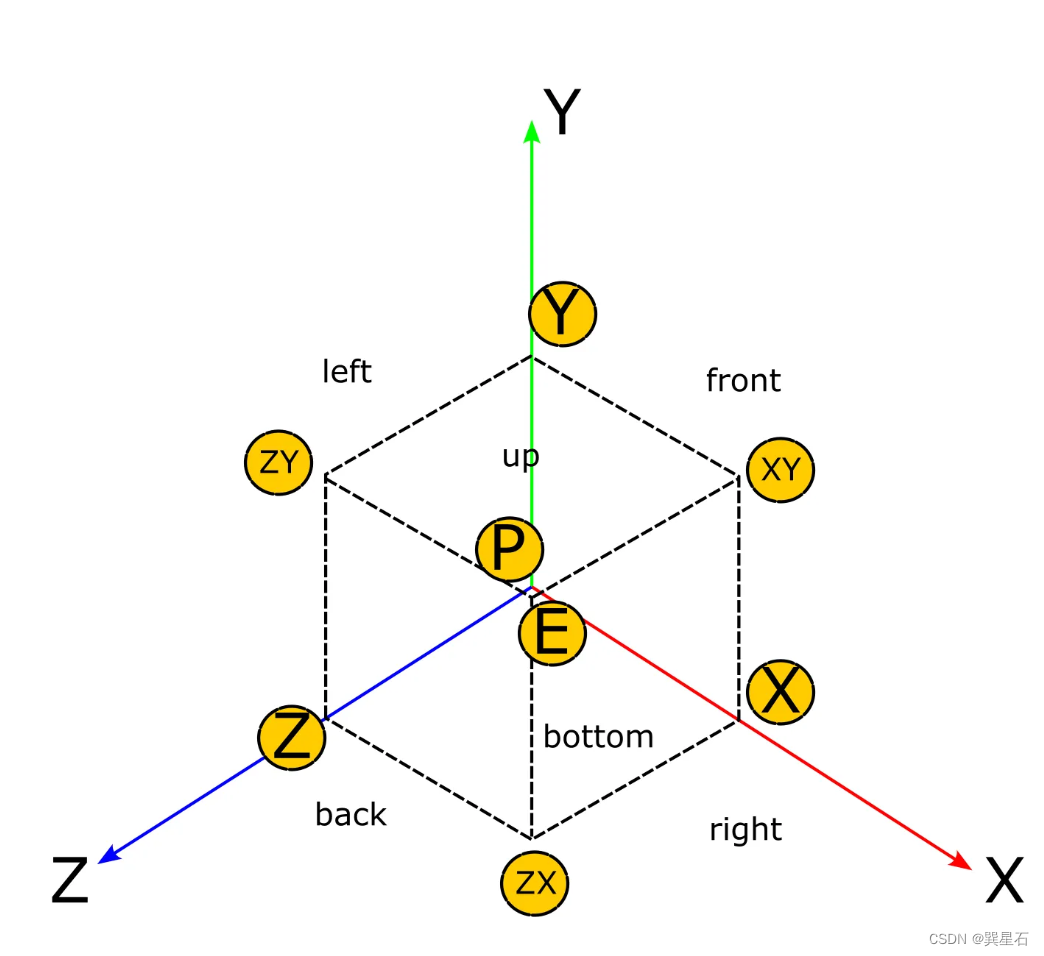

在这里插入图片描述

当实现一个立方体网格的绘制后，就可以基于此创建融并的网格。

创建融并网格和区域

@tool
extends EditorScriptfunc _run():var ins:MeshInstance3D = get_scene().get_node("MeshInstance3D")ins.mesh = create_area([Vector3.ZERO,Vector3.ONE])# 在area_pos_arr传入的所有3维空间位置创建一个16×16的立方体网格区域
func create_area(area_pos_arr:PackedVector3Array):var pos_arr:PackedVector3Arrayfor area_pos in area_pos_arr:# 以16×16为一个小区域var area_start_pos = area_pos * 16var area_size = Vector3.ONE * 16var box:AABB = AABB(area_start_pos,area_size)# 随机生成box位置for x in range(area_start_pos.x,box.end.x):for y in range(area_start_pos.y,box.end.y):for z in range(area_start_pos.z,box.end.z):var is_empty = randi_range(0,1)if not is_empty:pos_arr.append(Vector3(x,y,z))return create_cubemesh(pos_arr)# 在pos_arr传入的所有3维空间位置创建一个立方体网格
func create_cubemesh(pos_arr:PackedVector3Array):var st = SurfaceTool.new()st.begin(Mesh.PRIMITIVE_TRIANGLES)for pos in pos_arr:# 构造AABBvar size = Vector3.ONEvar box:AABB = AABB(pos,size)var end = box.end# ============= 获得立方体8个顶点的坐标# positon和andvar p_P = posvar p_E = end# 三条坐标轴方向的边的端点var p_Z = Vector3(pos.x,pos.y,end.z) # Z轴var p_Y = Vector3(pos.x,end.y,pos.z) # Y轴var p_X = Vector3(end.x,pos.y,pos.z) # X轴# 三个平面上的点的端点var p_YZ = Vector3(pos.x,end.y,end.z) # YZ平面var p_XZ = Vector3(end.x,pos.y,end.z) # XZ平面var p_XY = Vector3(end.x,end.y,pos.z) # XY平面# 6个顶点的UV坐标顺序var uvs = [Vector2.DOWN,Vector2.ZERO,Vector2.RIGHT,Vector2.ONE]# ============= 定义立方体6个面的法线和顶点绘制顺序# 右侧面var faces = {f_right = { # 右侧面normal = Vector3.RIGHT,vectors = [p_XZ,p_E,p_XY,p_X]},f_up = { # 上面normal = Vector3.UP,vectors = [p_E,p_YZ,p_Y,p_XY]},f_left = { # 左侧面normal = Vector3.LEFT,vectors = [p_P,p_Y,p_YZ,p_Z]},f_bottom = { # 底面normal = Vector3.DOWN,vectors = [p_Z,p_XZ,p_X,p_P]},f_front = { # 前面normal = Vector3.FORWARD,vectors = [p_X,p_XY,p_Y,p_P]},f_bcak = { # 后面normal = Vector3.BACK,vectors = [p_Z,p_YZ,p_E,p_XZ]}}# 检测上下左右前后方向有无立方体# 有的话就删除相应的面for face in faces:if pos + faces[face]["normal"] not in pos_arr:for i in [0,1,2,2,3,0]:st.set_normal(faces[face]["normal"])st.set_uv(uvs[i])st.add_vertex(faces[face]["vectors"][i])var mesh = st.commit()return mesh

运行后，将基于一个MeshInstance3D节点生成如下复杂的网格：
但是后期最好的做法是一个MeshInstance3D节点只生成一个16×16小区域的网格。
生成的两个区域的网格
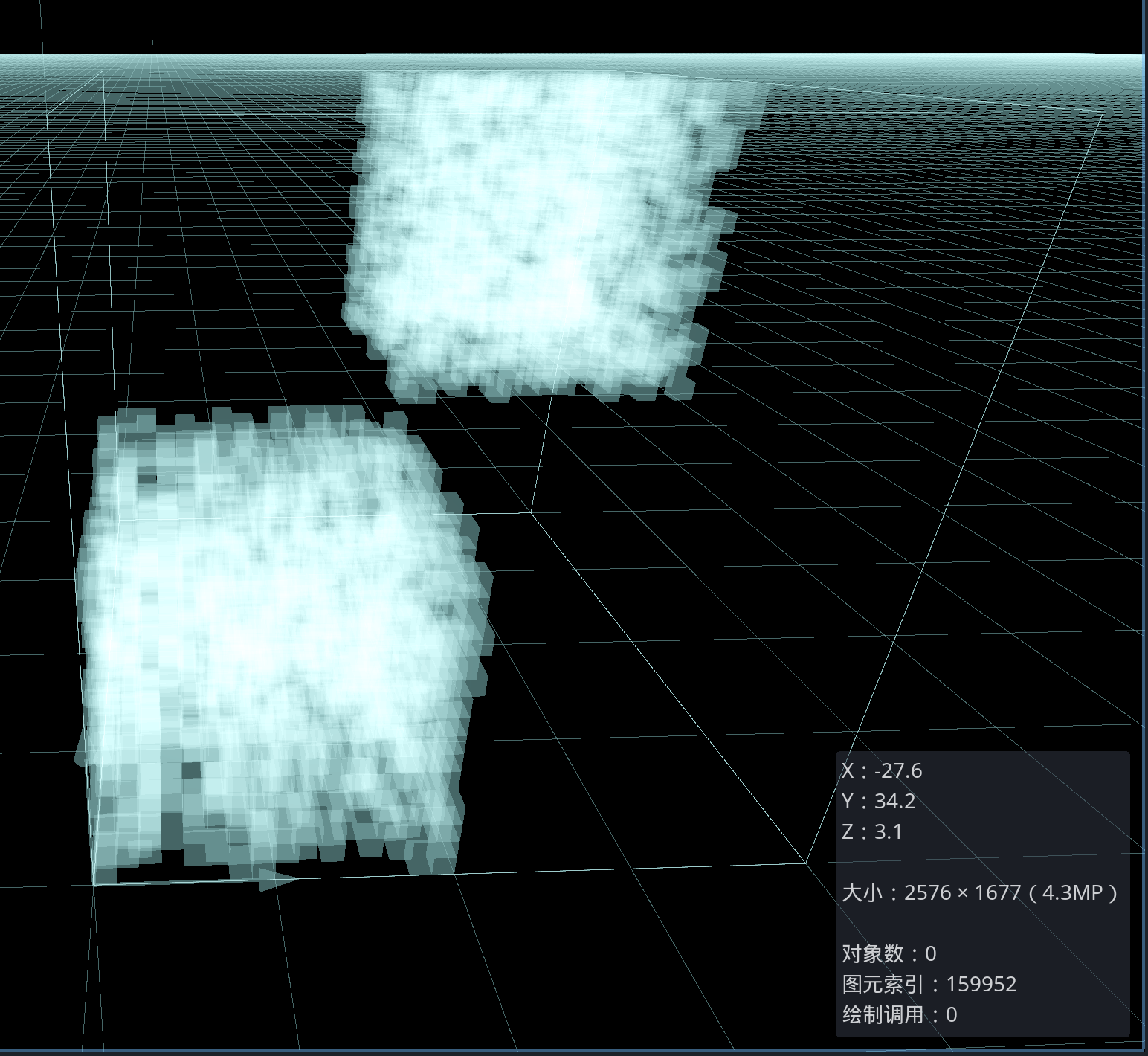
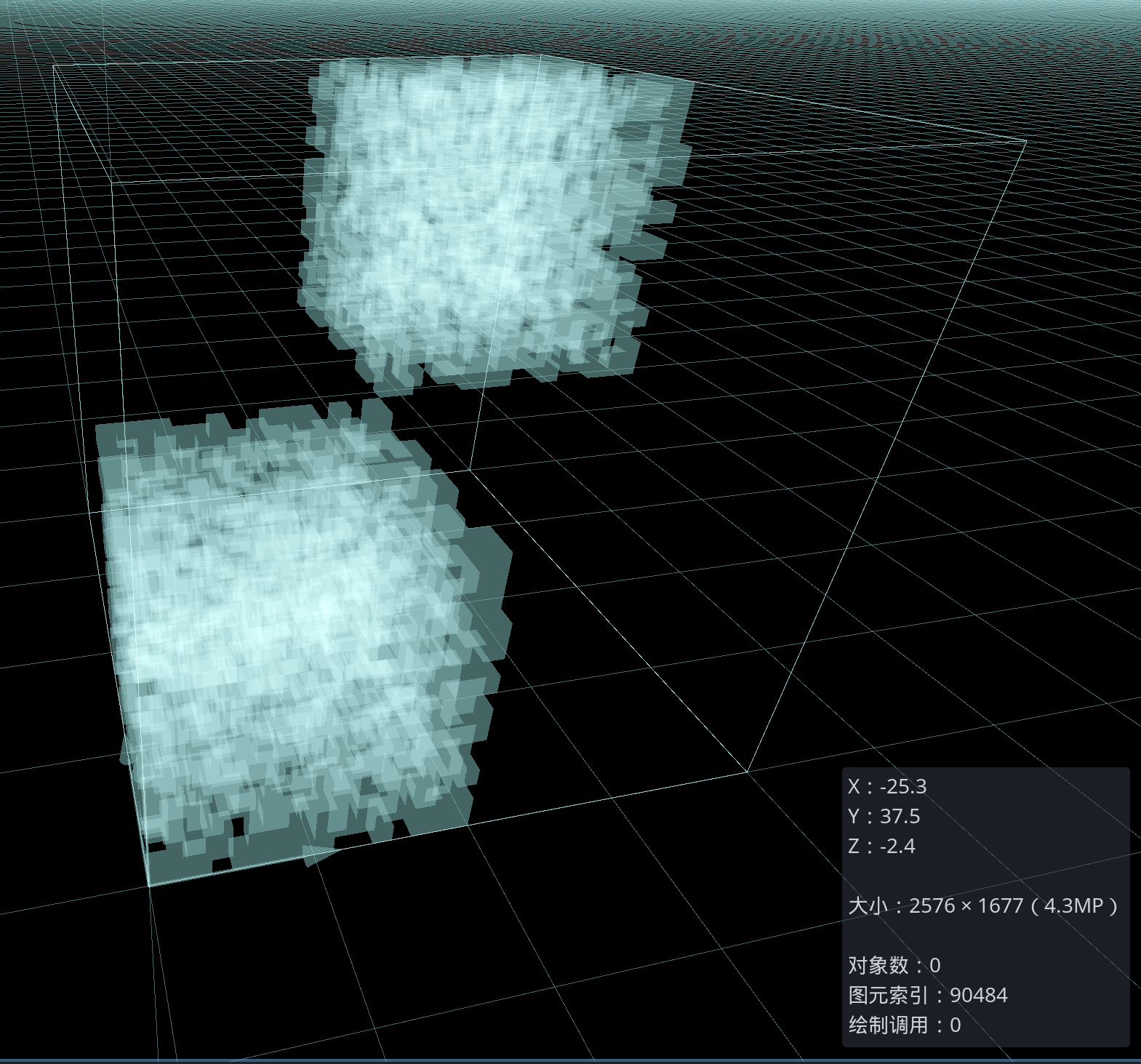
未采用网格融并算法采用了网格融并算法
对比之后可以看到，采用了融并网格算法生成的三角面数比没有采用的少了将近7000左右。

总结

本篇文章简单实现了一个体素融并网格的生成算法。
如果要实现类似Minecraft那样效果，就需要在每个16×16小区域内判定对某个位置的方块进行删除或添加。所谓的删除或添加也就是像数组添加或删除一个位置信息。然后重新生成这个区域的网格就行了。实际可能会更复杂一些。
另外在地形生成上可以使用随机地图生成技术中的柏林算法，应该可以获得更自然的效果。