文章目录
- 其他经典例题跳转链接
- 46.稀疏矩阵
- 47.多维矩阵转一维矩阵
- 48.上三角、下三角、对称矩阵
- 49.奇数魔方阵
- 50.4N 魔方阵
- 51.2(2N+1) 魔方阵
其他经典例题跳转链接
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-2
字串核对、双色、三色河内塔、背包问题(Knapsack Problem)、蒙地卡罗法求 PI、Eratosthenes筛选求质数
C语言经典算法-3
超长整数运算(大数运算)、长 PI、最大公因数、最小公倍数、因式分解、完美数、阿姆斯壮数
C语言经典算法-4
最大访客数、中序式转后序式(前序式)、后序式的运算、洗扑克牌(乱数排列)、Craps赌博游戏
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-6
数字拆解、得分排行,选择、插入、气泡排序、Shell 排序法 - 改良的插入排序、Shaker 排序法 - 改良的气泡排序
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
46.稀疏矩阵
说明
如果在矩阵中,多数的元素并没有资料,称此矩阵为稀疏矩阵(sparse matrix),由于矩阵在程式中常使用二维阵列表示,二维阵列的大小与使用的记忆体空间成正比,如果多数的元素没有资料,则会造成记忆体空间的浪费,为 此,必须设计稀疏矩阵的阵列储存方式,利用较少的记忆体空间储存完整的矩阵资讯。
解法
在这边所介绍的方法较为简单,阵列只储存矩阵的行数、列数与有资料的索引位置及其值,在需要使用矩阵资料时,再透过程式运算加以还原,例如若矩阵资料如下 ,其中0表示矩阵中该位置没有资料:
0 0 0 0 0 0
0 3 0 0 0 0
0 0 0 6 0 0
0 0 9 0 0 0
0 0 0 0 12 0
这个矩阵是5X6矩阵,非零元素有4个,您要使用的阵列第一列记录其列数、行数与非零元素个数:
5 6 4
阵列的第二列起,记录其位置的列索引、行索引与储存值:
1 1 3
2 3 6
3 2 9
4 4 12
所以原本要用30个元素储存的矩阵资讯,现在只使用了15个元素来储存,节省了不少记忆体的使用。
#include <stdio.h>
#include <stdlib.h> int main(void) { int num[5][3] = {{5, 6, 4}, {1, 1, 3}, {2, 3, 6}, {3, 2, 9}, {4, 4, 12}}; int i, j, k = 1; printf("sparse matrix:\n"); for(i = 0; i < 5; i++) { for(j = 0; j < 3; j++) { printf("%4d", num[i][j]); } putchar('\n'); } printf("\nmatrix还原:\n"); for(i = 0; i < num[0][0]; i++) { for(j = 0; j < num[0][1]; j++) { if(k < num[0][2] && i == num[k][0] && j == num[k][1]) { printf("%4d ", num[k][2]); k++; } else printf("%4d ", 0); } putchar('\n'); } return 0;
}
47.多维矩阵转一维矩阵
说明
有的时候,为了运算方便或资料储存的空间问题,使用一维阵列会比二维或多维阵列来得方便,例如上三角矩阵、下三角矩阵或对角矩阵,使用一维阵列会比使用二维阵列来得节省空间。
解法
以二维阵列转一维阵列为例,索引值由0开始,在由二维阵列转一维阵列时,我们有两种方式:「以列(Row)为主」或「以行(Column)为主」。由于 C/C++、Java等的记忆体配置方式都是以列为主,所以您可能会比较熟悉前者(Fortran的记忆体配置方式是以行为主)。
以列为主的二维阵列要转为一维阵列时,是将二维阵列由上往下一列一列读入一维阵列,此时索引的对应公式如下所示,其中row与column是二维阵列索引,loc表示对应的一维阵列索引:
loc = column + row*行数
以行为主的二维阵列要转为一维阵列时,是将二维阵列由左往右一行一行读入一维阵列,此时索引的对应公式如下所示:
loc = row + column*列数
公式的推导您画图看看就知道了,如果是三维阵列,则公式如下所示,其中i(个数u1)、j(个数u2)、k(个数u3)分别表示三维阵列的三个索引:
以列为主:loc = iu2u3 + ju3 + k
以行为主:loc = ku1u2 + ju1 + i
更高维度的可以自行依此类推,但通常更高维度的建议使用其它资料结构(例如物件包装)会比较具体,也不易搞错。
在C/C++中若使用到指标时,会遇到指标运算与记忆体空间位址的处理问题,此时也是用到这边的公式,不过必须在每一个项上乘上资料型态的记忆体大小。
#include <stdio.h>
#include <stdlib.h> int main(void) { int arr1[3][4] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}}; int arr2[12] = {0}; int row, column, i; printf("原二维资料:\n"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { printf("%4d", arr1[row][column]); } printf("\n"); } printf("\n以列为主:"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { i = column + row * 4; arr2[i] = arr1[row][column]; } } for(i = 0; i < 12; i++) printf("%d ", arr2[i]); printf("\n以行为主:"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { i = row + column * 3; arr2[i] = arr1[row][column]; } } for(i = 0; i < 12; i++) printf("%d ", arr2[i]); printf("\n"); return 0;
}
48.上三角、下三角、对称矩阵
说明
上三角矩阵是矩阵在对角线以下的元素均为0,即Aij = 0,i > j,例如:
1 2 3 4 5
0 6 7 8 9
0 0 10 11 12
0 0 0 13 14
0 0 0 0 15
下三角矩阵是矩阵在对角线以上的元素均为0,即Aij = 0,i < j,例如:
1 0 0 0 0
2 6 0 0 0
3 7 10 0 0
4 8 11 13 0
5 9 12 14 15
对称矩阵是矩阵元素对称于对角线,例如:
1 2 3 4 5
2 6 7 8 9
3 7 10 11 12
4 8 11 13 14
5 9 12 14 15
上三角或下三角矩阵也有大部份的元素不储存值(为0),我们可以将它们使用一维阵列来储存以节省储存空间,而对称矩阵因为对称于对角线,所以可以视为上三角或下三角矩阵来储存。
解法
假设矩阵为nxn,为了计算方便,我们让阵列索引由1开始,上三角矩阵化为一维阵列,若以列为主,其公式为:loc = n*(i-1) - i*(i-1)/2 + j
化为以行为主,其公式为:loc = j*(j-1)/2 + i
下三角矩阵化为一维阵列,若以列为主,其公式为:loc = i*(i-1)/2 + j
若以行为主,其公式为:loc = n*(j-1) - j*(j-1)/2 + i
公式的导证其实是由等差级数公式得到,您可以自行绘图并看看就可以导证出来,对于C/C++或Java等索引由0开始的语言来说,只要将i与j各加1,求得loc之后减1即可套用以上的公式。
#include <stdio.h>
#include <stdlib.h>
#define N 5 int main(void) { int arr1[N][N] = { {1, 2, 3, 4, 5}, {0, 6, 7, 8, 9}, {0, 0, 10, 11, 12}, {0, 0, 0, 13, 14}, {0, 0, 0, 0, 15}}; int arr2[N*(1+N)/2] = {0}; int i, j, loc = 0; printf("原二维资料:\n"); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { printf("%4d", arr1[i][j]); } printf("\n"); } printf("\n以列为主:"); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(arr1[i][j] != 0) arr2[loc++] = arr1[i][j]; } } for(i = 0; i < N*(1+N)/2; i++) printf("%d ", arr2[i]); printf("\n输入索引(i, j):"); scanf("%d, %d", &i, &j); loc = N*i - i*(i+1)/2 + j; printf("(%d, %d) = %d", i, j, arr2[loc]); printf("\n"); return 0;
}
49.奇数魔方阵
说明
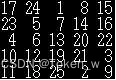
将1到n(为奇数)的数字排列在nxn的方阵上,且各行、各列与各对角线的和必须相同,如下所示:
解法
填魔术方阵的方法以奇数最为简单,第一个数字放在第一行第一列的正中央,然后向右(左)上填,如果右(左)上已有数字,则向下填,如下图所示:
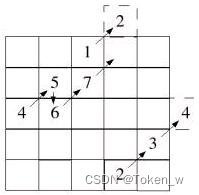
一般程式语言的阵列索引多由0开始,为了计算方便,我们利用索引1到n的部份,而在计算是向右(左)上或向下时,我们可以将索引值除以n值,如果得到余数为1就向下,否则就往右(左)上,原理很简单,看看是不是已经在同一列上绕一圈就对了。
#include <stdio.h>
#include <stdlib.h> #define N 5 int main(void) { int i, j, key; int square[N+1][N+1] = {0}; i = 0; j = (N+1) / 2; for(key = 1; key <= N*N; key++) { if((key % N) == 1) i++; else { i--; j++; } if(i == 0) i = N; if(j > N) j = 1; square[i][j] = key; } for(i = 1; i <= N; i++) { for(j = 1; j <= N; j++) printf("%2d ", square[i][j]); } return 0;
}
50.4N 魔方阵
说明
与 奇数魔术方阵 相同,在于求各行、各列与各对角线的和相等,而这次方阵的维度是4的倍数。
解法
先来看看4X4方阵的解法:
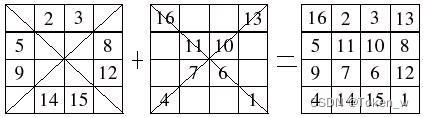
简单的说,就是一个从左上由1依序开始填,但遇对角线不填,另一个由左上由16开始填,但只填在对角线,再将两个合起来就是解答了;如果N大于2,则以 4X4为单位画对角线:
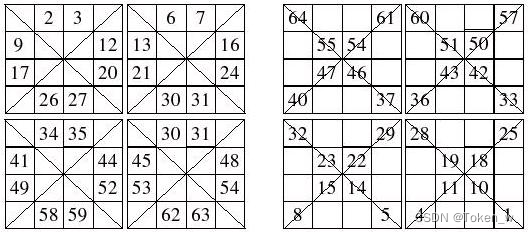
至于对角线的位置该如何判断,有两个公式,有兴趣的可以画图印证看看,如下所示:
左上至右下:j % 4 == i % 4
右上至左下:(j % 4 + i % 4) == 1
#include <stdio.h>
#include <stdlib.h> #define N 8 int main(void) { int i, j; int square[N+1][N+1] = {0}; for(j = 1; j <= N; j++) { for(i = 1; i <= N; i++){ if(j % 4 == i % 4 || (j % 4 + i % 4) == 1) square[i][j] = (N+1-i) * N -j + 1; else square[i][j] = (i - 1) * N + j; } } for(i = 1; i <= N; i++) { for(j = 1; j <= N; j++) printf("%2d ", square[i][j]); printf("\n"); } return 0;
}
51.2(2N+1) 魔方阵
说明方阵的维度整体来看是偶数,但是其实是一个奇数乘以一个偶数,例如6X6,其中6=2X3,我们也称这种方阵与单偶数方阵。
解法如果您会解奇数魔术方阵,要解这种方阵也就不难理解,首先我们令n=2(2m+1),并将整个方阵看作是数个奇数方阵的组合,如下所示:
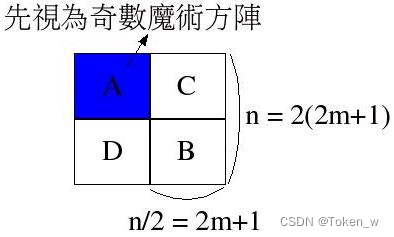
首先依序将A、B、C、D四个位置,依奇数方阵的规则填入数字,填完之后,方阵中各行的和就相同了,但列与对角线则否,此时必须在A-D与C- B之间,作一些对应的调换,规则如下:
将A中每一列(中间列除外)的头m个元素,与D中对应位置的元素调换。
将A的中央列、中央那一格向左取m格,并与D中对应位置对调
将C中每一列的倒数m-1个元素,与B中对应的元素对调
举个实例来说,如何填6X6方阵,我们首先将之分解为奇数方阵,并填入数字,如下所示:
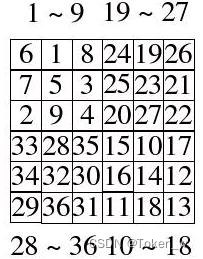
接下来进行互换的动作,互换的元素以不同颜色标示,如下:
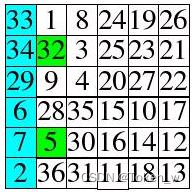
由于m-1的数为0,所以在这个例子中,C-B部份并不用进行对调。
#include <stdio.h>
#include <stdlib.h> #define N 6
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void magic_o(int [][N], int);
void exchange(int [][N], int); int main(void) { int square[N][N] = {0}; int i, j; magic_o(square, N/2); exchange(square, N); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) printf("%2d ", square[i][j]); printf("\n"); } return 0;
} void magic_o(int square[][N], int n) { int count, row, column; row = 0; column = n / 2; for(count = 1; count <= n*n; count++) { square[row][column] = count; // 填A square[row+n][column+n] = count + n*n; // 填B square[row][column+n] = count + 2*n*n; // 填C square[row+n][column] = count + 3*n*n; // 填D if(count % n == 0) row++; else { row = (row == 0) ? n - 1 : row - 1 ; column = (column == n-1) ? 0 : column + 1; } }
} void exchange(int x[][N], int n) { int i, j; int m = n / 4; int m1 = m - 1; for(i = 0; i < n/2; i++) { if(i != m) { for(j = 0; j < m; j++) // 处理规则 1 SWAP(x[i][j], x[n/2+i][j]); for(j = 0; j < m1; j++) // 处理规则 2 SWAP(x[i][n-1-j], x[n/2+i][n-1-j]); } else { // 处理规则 3 for(j = 1; j <= m; j++) SWAP(x[m][j], x[n/2+m][j]); for(j = 0; j < m1; j++) SWAP(x[m][n-1-j], x[n/2+m][n-1-j]); } }
}
系列好文,点击链接即可跳转
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法