1.前言

哪些情况下会用到动态规划：

1.最优化问题：当需要求解最大值或最小值的问题时，可以考虑使用动态规划。例如，最长递增子序列、最短路径问题等。

2.问题具有重叠子问题性质：如果问题的解可以由其子问题的解构成，并且子问题之间存在重叠，即同一个子问题会被多次求解，那么可以使用动态规划。通过将子问题的解保存下来，避免重复计算，提高效率。

3.问题具有最优子结构性质：如果问题的最优解可以由其子问题的最优解推导得出，那么可以使用动态规划。通过递推关系式，将问题分解为子问题，并利用子问题的最优解来构造原问题的最优解。

4.求解过程具有重叠子结构性质：如果问题的求解过程中，需要多次用到相同的中间结果，那么可以使用动态规划。通过保存中间结果，避免重复计算，提高效率。

5.多阶段决策问题：当问题可以划分为多个阶段，并且每个阶段的决策依赖于之前阶段的决策结果时，可以使用动态规划。通过定义状态和状态转移方程，逐步求解每个阶段的最优解。

2. 示例 - 第N个泰波那契数

题目地址：点这里

2.1 算法原理（重点）

空间优化（选）：

• 背包问题
• 滚动数组

---

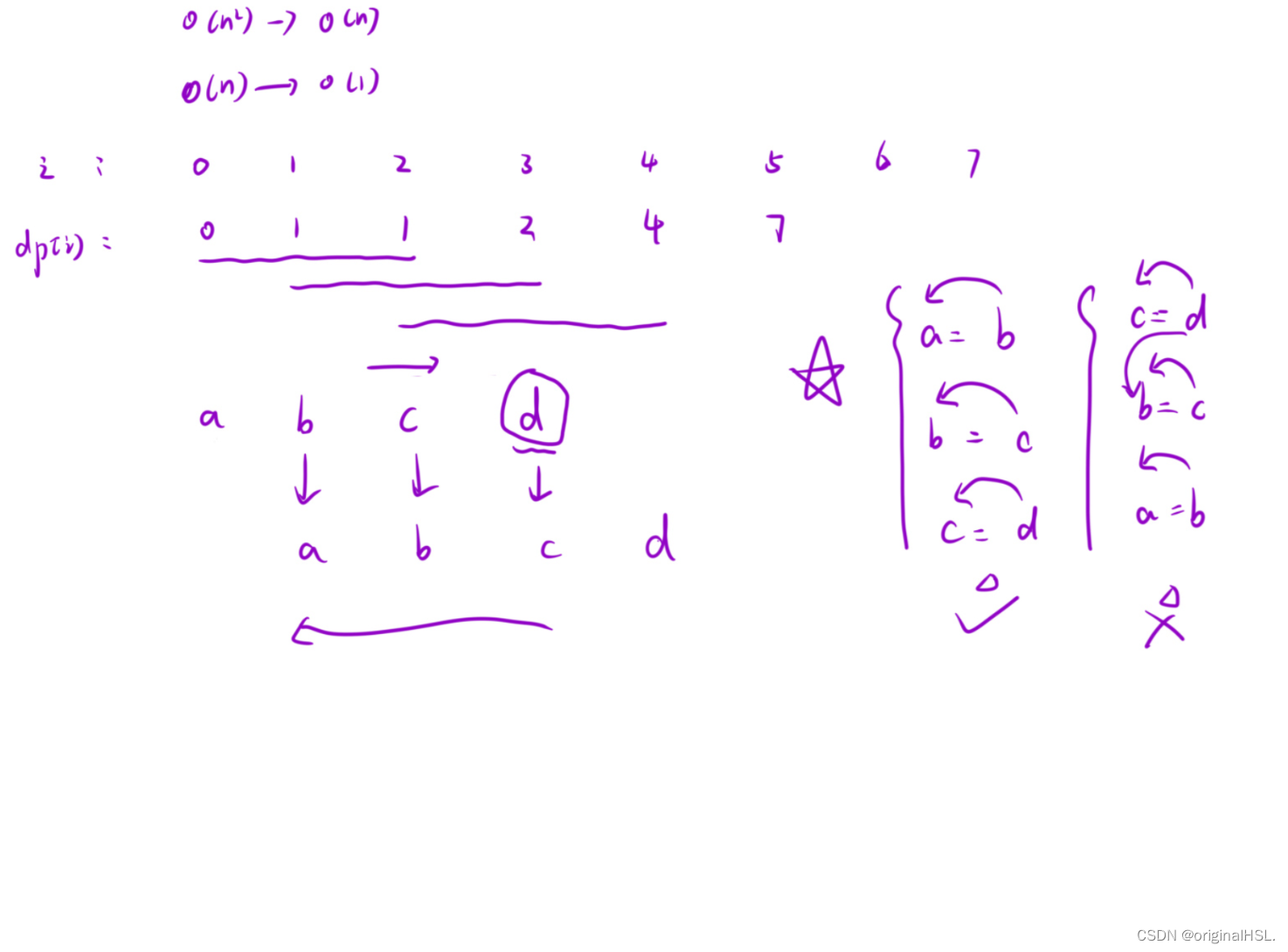
1. 创建一个长度为38的数组arr，用于存储计算过程中的中间结果。数组的下标表示泰波那契数的序号，数组元素存储对应序号的泰波那契数的值。

2. 初始化数组的前三个元素arr[0]、arr[1]和arr[2]分别为0、1、1，这是泰波那契数列的起始值。

3. 如果n小于等于2，直接返回arr[n]，即泰波那契数列的前三个数。

4. 从i=3开始，通过循环填充数组arr的剩余元素。对于每个i，计算泰波那契数arr[i]的值，它等于前三个数的和arr[i-3] + arr[i-2] + arr[i-1]。

5. 循环结束后，数组arr中的所有泰波那契数都已计算得到。

6. 返回arr[n]，即第n个泰波那契数的值。

---

2.2 代码

class Solution {
public:int tribonacci(int n) {//1.创建dp表int arr[38]={0};//2.初始化arr[0]=0,arr[1]=1,arr[2]=1;if(n<=2) return arr[n];int temp=0;//3.填表for(int i=3;i<=n;i++){temp=arr[i-3]+arr[i-2]+arr[i-1];arr[i]=temp;}//4.返回值return arr[n];}
};

3. 总结解题思路

---

1. 状态表示
2. 状态转移方程
3. 初始化
4. 填表顺序
5. 返回值

---