问题预览
1.本节课主要讲的是什么?
2.不同的w和b,如何影响线性回归和等高线图?
3.一般用哪种方式,可以找到最佳的w和b?
解读
1.课程内容
设置不同的w和b,观察模型拟合数据,成本函数J的等高线图,三维空间图。
2.不同的w和b,对应的线性回归和等高线图(可视化)
示例1:参数w≈-0.15,参数b≈-800。
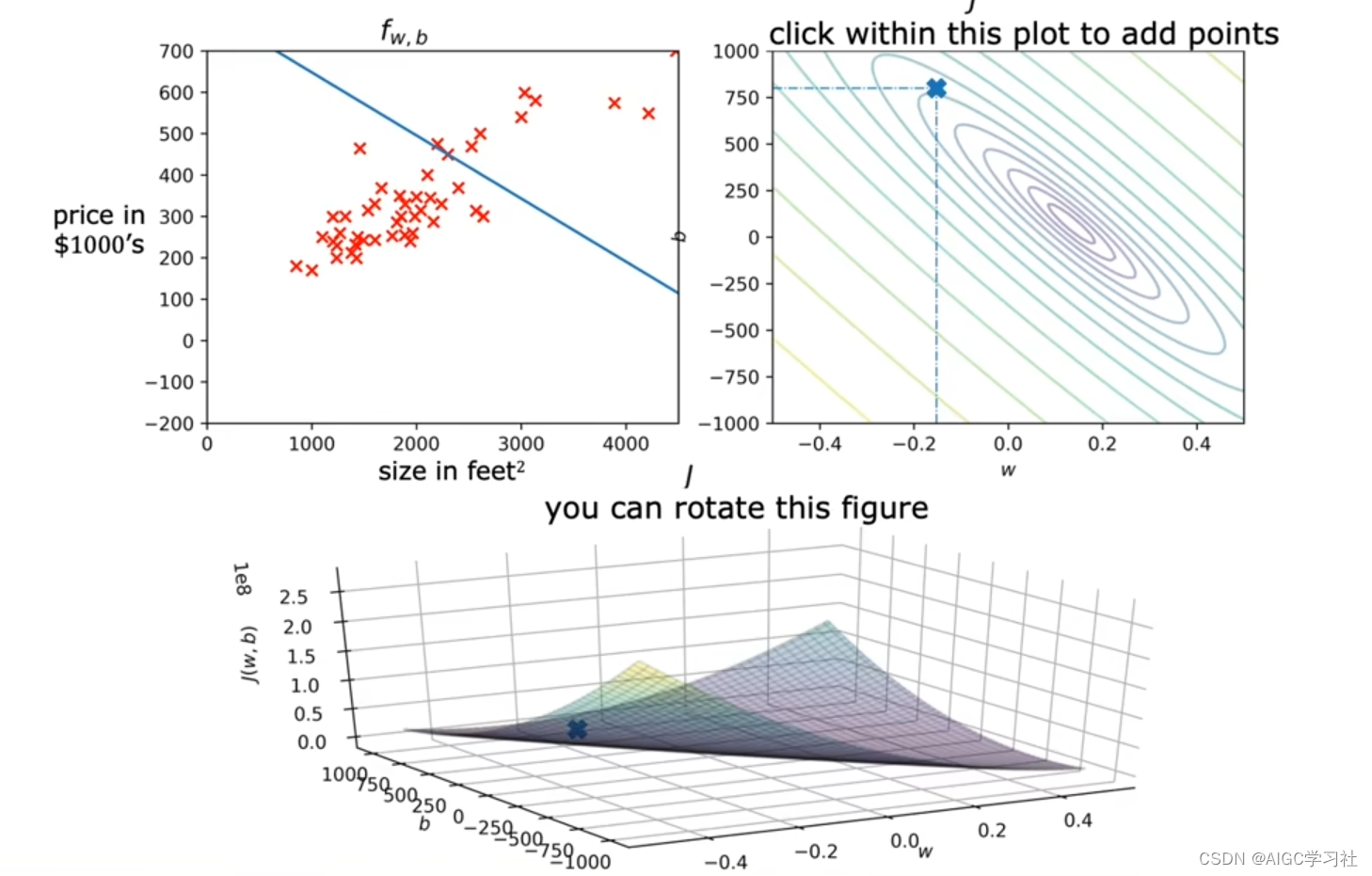
w≈-0.15,b≈-800构建的线性回归,拟合数据的效果欠佳。
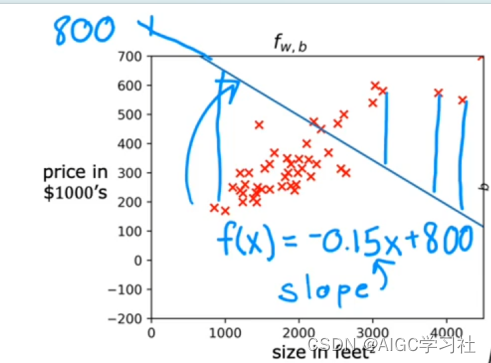
w,b坐标远离等高线图的中心圈,成本函数未最小化,误差大。
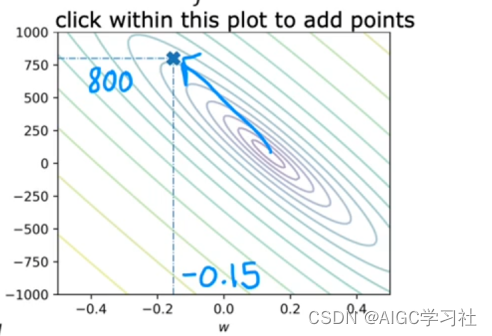
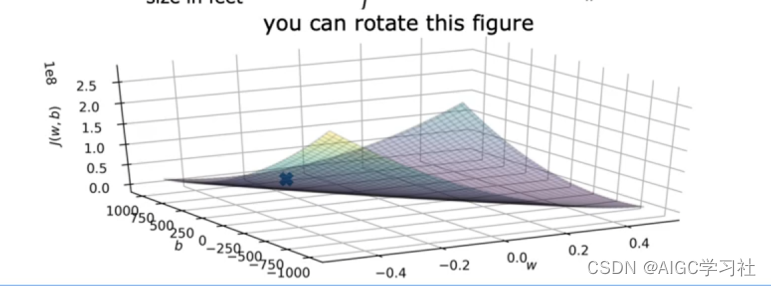
w,b在三维空间的坐标。
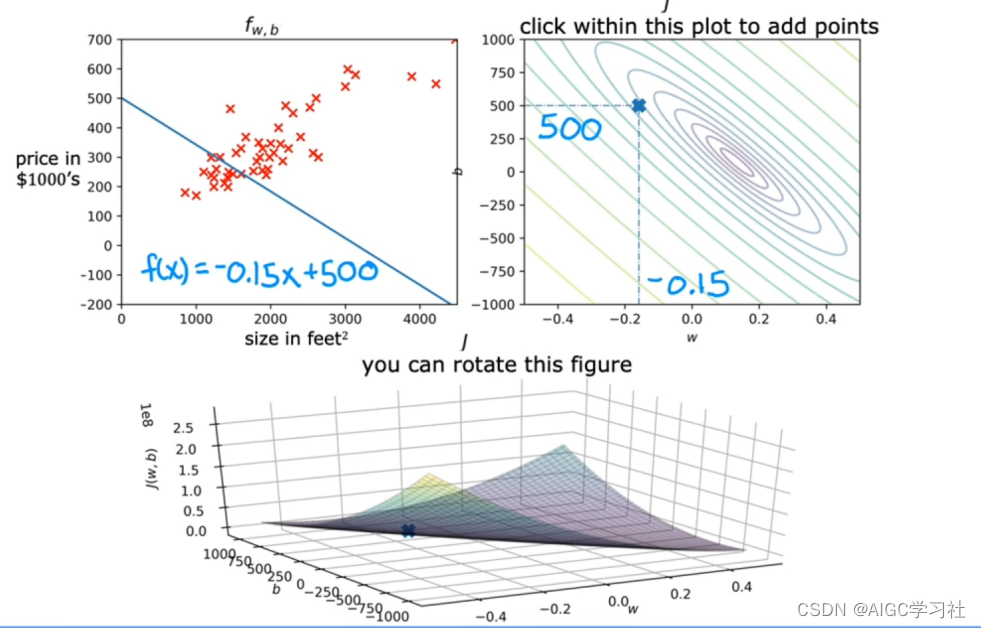
示例2:参数w约等于-0.15,参数b约等于-800。

w,b构建的线性回归,拟合数据的效果依旧欠佳。
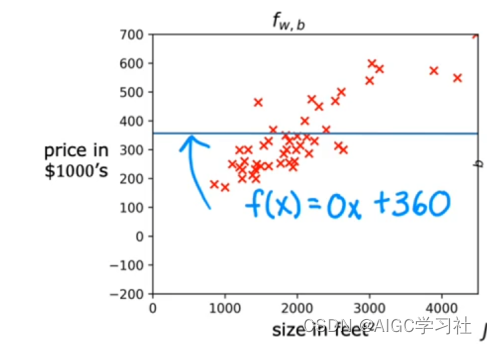
w,b坐标接近但没有达到等高线图的中心圈,仍未最小化成本函数,有误差。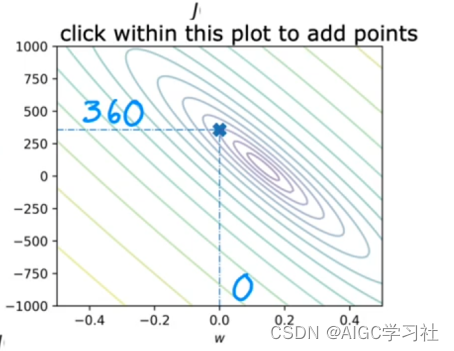
w,b在三维空间的坐标。
示例3:w,b坐标依旧没在等高线图的中心圈,未最小化成本函数,因此线性回归拟合数据的效果不好。
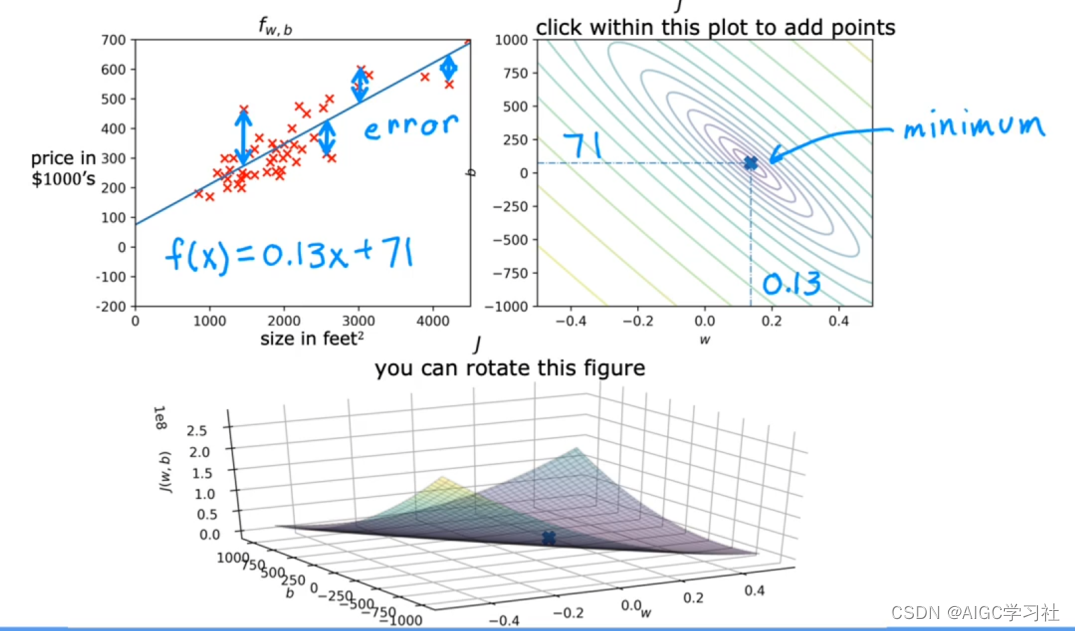
示例4:w≈0.13,b≈71,w,b在等高线图的坐标是中心圈,对应三维空间图的最低点,最小化了成本函数,因此拟合数据效果最好。
总结
了解不同的w,b,如何影响线性回归的直线以及成本函数J。
等高线图无法满足复杂的机器学习模型,一般需要梯度下降算法,自动计算最佳的w和b。