目录

 回文子串

最长回文子串

 分割回文串 IV

 分割回文串 II

 最长回文子序列

 让字符串成为回文串的最少插入次数

---

 回文子串

647. 回文子串

思路，i  j表示改范围内是否为回文串，

②倒着遍历是为了取出dp[i + 1][j - 1]

③i j 只有一对，不会重复，其实就是遍历

参考代码

class Solution {
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for(int i = n - 1; i >= 0; i--){// dp[i][i] = true;// for(int j = i + 1; j < n; j++)// {//     if(s[i] == s[j])//         dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;//     if(dp[i][j]) ret++;//判断每一次// }for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;//只有最后一层会越界，但是if(dp[i][j])ret++;}}// return ret + n;return ret;}
};

最长回文子串

5. 最长回文子串

思路区间[i,  j] 是true时候再判断

参考代码

class Solution {
public:string longestPalindrome(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));int maxlen = 1, begin = 0;for(int i = n - 1; i >= 0; i--){dp[i][i] = true;for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;if(dp[i][j] && j - i + 1 > maxlen)maxlen = j - i + 1, begin = i;}}return s.substr(begin, maxlen);}
};

 分割回文串 IV

1745. 分割回文串 IV

用区间[i, j]即可分成三段 ，只要i j 不同，三段必不相同

参考代码

class Solution {
public:bool checkPartitioning(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;for(int i = 1; i <= n - 2; i++)for(int j = i; j <= n - 2; j++)if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])return true;return false;}
};

 分割回文串 II

132. 分割回文串 II

刚开始打算用dp[i, j]区间内需要的次数 ，发现逻辑就不对，以左右单个字符拎出来，在min剩下的，最小分割的位置很可能在中间某个位置；所以打算重新遍历数组，和139. 单词拆分的思路很像，[0, i] 区间存放的就是最小分割次数

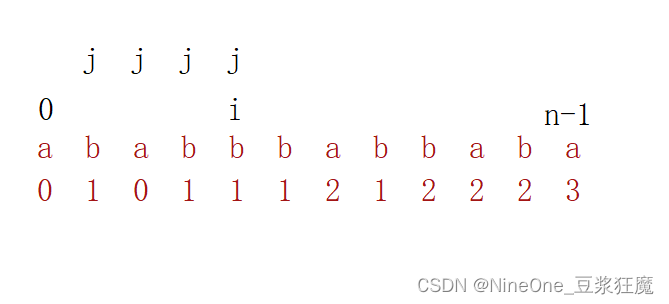
参考代码

class Solution {
public:int minCut(string s) {// int n = s.size();// vector<vector<int>> dp(n, vector<int>(n));// for(int i = n - 1; i >= 0; i--)// {//     for(int j = i + 1; j < n; j++)//     {//         if(s[i] == s[j])//             dp[i][j] = dp[i + 1][j - 1];//         else//             dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;//     }// }// return dp[0][n - 1];int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j]) dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;vector<int> times(n, INT_MAX);times[0] = 0;for(int i = 1; i < n; i++){if(dp[0][i]) times[i] = 0;elsefor(int j = 1; j <= i; j++)if(dp[j][i])times[i] = min(times[i], times[j - 1] + 1);}return times[n - 1];}
};

 最长回文子序列

516. 最长回文子序列

 

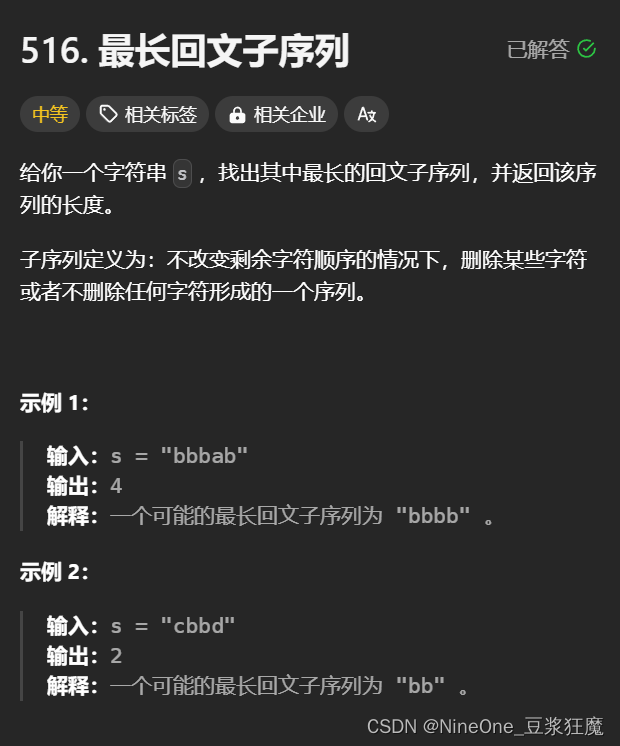
 因为[i ,j] 表示的是区间内的最长回文子序列，这里我不怎么能直接理解，这里的j每次往后走，应该是去尝试匹配s[i]，那么有人会说s[i] 可能和[i + 1, j - 1] 区间内有匹配了，那么用s[j]去匹配，不就少了一个吗？其实不然，这时候中间不管是否和s[i]相同,【 s[i] ,中间字符，s[j] 】就是一个回文子序列，这样是最大的；如果不相等，因为说了，状态表示的是区间内的最长回文子序列，这时候去已经有的区间里面找最长的已知区间就是[i + 1, j] 和 [i , j + 1]，那为什么不去[i, j] 里找，因为没有啊，这时候，dp[i][j]是左值呀

参考代码

class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n, 1));for(int i = n - 1; i >= 0; i--){for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] + 2 : j - i + 1;elsedp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}return dp[0][n - 1];}
};

 让字符串成为回文串的最少插入次数

 1312. 让字符串成为回文串的最少插入次数

 

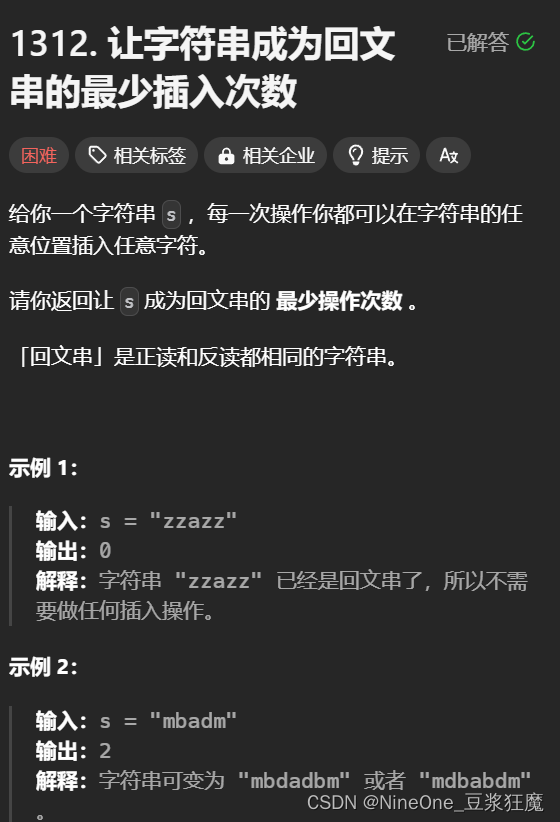
 dp表示的是区间[i,  j] 内需要添加的最小次数，同样的道理，如果不相等就是去消除s[i] 或者s[j]，消除伴随着 +1，也就是dp[i][j] = min(dp[i][j - 1], dp[i + 1][j]) + 1,你可能会感觉不对，  有可能是min(dp[i][j - 2], dp[i + 2][j])那么随之后面就要+2，但是这个时候可能s[i] 和s[j - 1]是相等的啊，那么就多添加了一个字符

参考代码

class Solution {
public:int minInsertions(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for(int i = n - 1; i >= 0; i--){for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = dp[i + 1][j - 1];elsedp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;}}return dp[0][n - 1];}
};

总结:通过区间[i,  j]来表示每个区间是否为回文串 ，是的话在进行怎样怎样的操作

我的错误发生： i总是写错i++, 注意力不集中