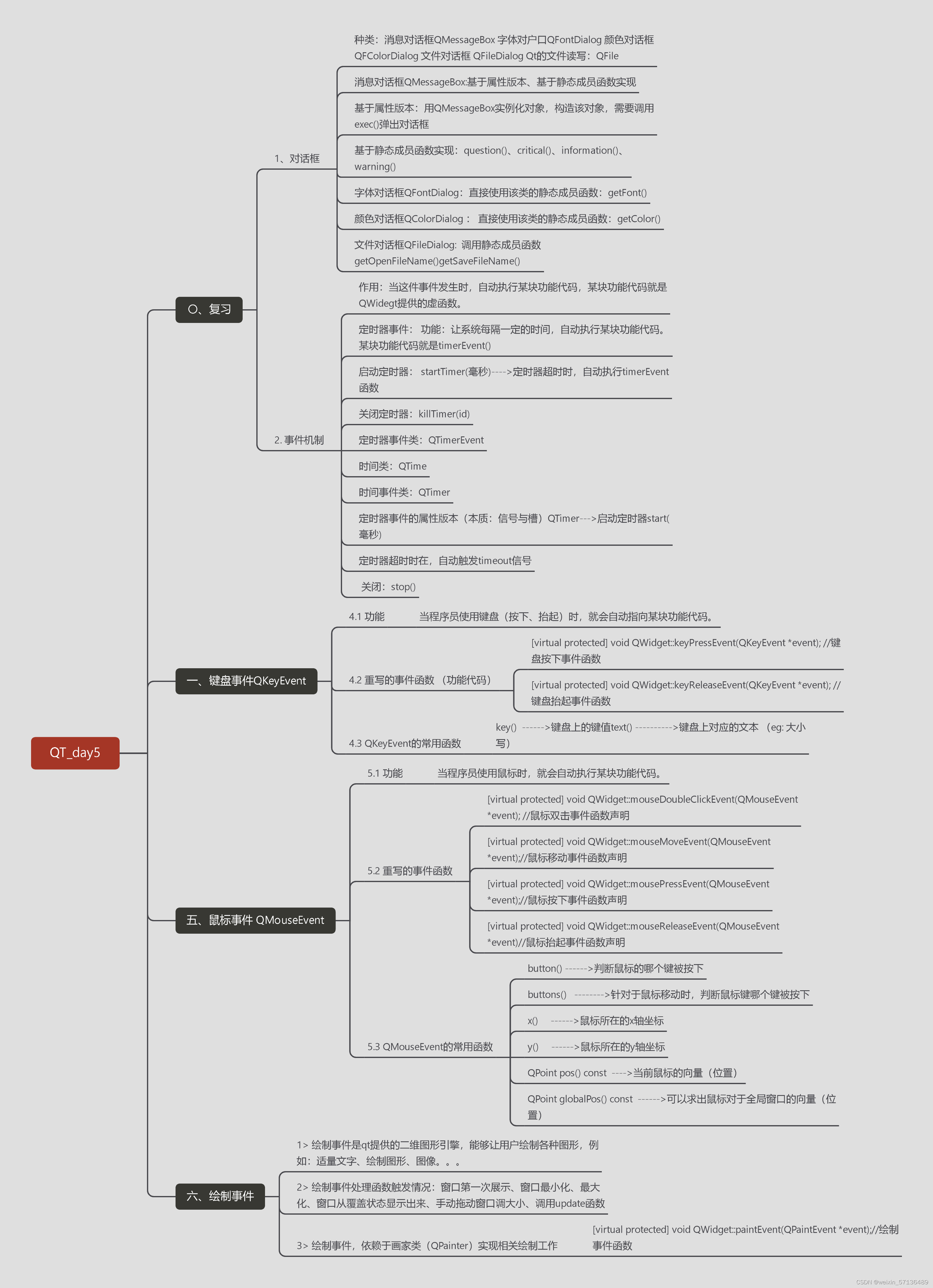
题目链接
本题是2010年ICPC亚洲区域赛东京赛区的I题
题意
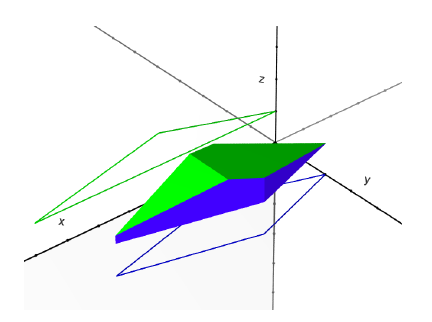
求两个无限高棱柱的交。其中一个棱柱是把xy平面上的凸多边形沿z轴无限拉长得到,另外一个棱柱是把xz平面上的凸多边形沿y轴无限拉长得到。输入给出第一个棱柱在xy平面的凸多边形坐标和另外一个棱柱在xz平面的凸多边形坐标,输出相交部分的体积。


分析
对第一个棱柱,依次枚举其凸多边形的每条边,对应一个平行于z轴的无限大矩形,求出此矩形与第二个棱柱相交得到的多边形。同样地依次枚举第二个棱柱凸多边形的每条边,对应一个平行于y轴的无限大矩形,求出此矩形与第一个棱柱相交得到的多边形。
这样就求出了相交多面体的每一个面,取相交多面体的第一个面的首个顶点,求此点与各个面的混合积之和,再除以6就是答案。
需要注意的点:枚举第一个棱柱的侧面(都是平行于z轴的面)和枚举第二个棱柱的侧面(都是平行于y轴的面)时可能产生相同的面,需要去重,平行于z轴的面和平行于y轴的面如果进一步都是垂直于x轴则可能重合。
再说一个时效可以优化的点:在枚举棱柱侧面求相交多面体的每个面过程中,找出了在xy面或者xz面上的投影多边形(特殊情况垂直于x轴时可快捷计算出yz面上结果矩形),不需要反投影得到真实的三维多边形(即不需要插值计算第三个轴的坐标),因为知道投影多边形与真实多边形的夹角a,投影多边形面积除以cos(a)就是真实多边形的面积。
具体来说,比如在枚举第一个棱柱的侧面边(x[i],z[i])(x[i+1],z[i+1])时,求dx=x[i+1]-x[i],dz=z[i+1]-z[i],则cos(a)=dx/sqrt(dx*dx+dz*dz)。不过这种方法仍然需要求出真实多边形的一个三维顶点和法向量,用于最终求混合积,整体的计算代价减小约1/3。
更多繁琐细节,参见AC代码。
AC代码
#include <iostream>
#include <iomanip>
using namespace std;#define eps 1e-10
#define N 105
int x1[N], y1[N], x2[N], z2[N]; int m, n, t, e;
struct Point3 {double x, y, z;Point3(double x = 0., double y = 0., double z = 0.): x(x), y(y), z(z) {}
} p[N], s[N<<1], q[N<<1], f[N];
typedef Point3 Vector3;Vector3 operator+ (const Vector3& A, const Vector3& B) {return Vector3(A.x + B.x, A.y + B.y, A.z + B.z);
}Vector3 operator- (const Vector3& A, const Vector3& B) {return Vector3(A.x - B.x, A.y - B.y, A.z - B.z);
}int dcmp(double x) {return abs(x) < eps ? 0 : (x < 0. ? -1 : 1);
}bool operator== (const Point3& a, const Point3& b) {return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0 && dcmp(a.z - b.z) == 0;
}double Dot(const Vector3& A, const Vector3& B) {return A.x * B.x + A.y * B.y + A.z * B.z;
}Vector3 Cross(const Vector3& A, const Vector3& B) {return Vector3(A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
}Vector3 Area2(const Point3* p, int n) {Vector3 s;for (int i=n-2; i>0; --i) s = s + Cross(p[i]-p[0], p[i+1]-p[0]);return s;
}double interp(int x1, int y1, int x2, int y2, double x) {return ((x-x1)*y2 + (x2-x)*y1) / (x2-x1);
}bool find(const Point3& p) {for (int i=0; i<e; ++i) if (f[i] == p) return true;return false;
}double solve() {for (int i=0; i<m; ++i) cin >> x1[i] >> y1[i];for (int i=0; i<n; ++i) cin >> x2[i] >> z2[i];x1[m] = x1[0]; y1[m] = y1[0]; x2[n] = x2[0]; z2[n] = z2[0];for (int i=t=e=0; i<m; ++i) {int a = min(x1[i], x1[i+1]), b = max(x1[i], x1[i+1]), c = 0;if (a == b) {for (int j=0; j<n; ++j) {int l = min(x2[j], x2[j+1]), r = max(x2[j], x2[j+1]);if (a < l || a > r) continue;if (a == x2[j]) p[c].x = a, p[c].y = y1[i], p[c++].z = z2[j];else if (a != x2[j+1])p[c].x = a, p[c].y = y1[i], p[c++].z = interp(x2[j], z2[j], x2[j+1], z2[j+1], a);}if (c == 2) {p[2].x = p[3].x = a; p[2].y = p[3].y = y1[i+1]; p[2].z = p[1].z; p[3].z = p[0].z; c = 4;f[e].x = a; f[e].y = (y1[i] + y1[i+1]) / 2.; f[e++].z = (p[0].z + p[1].z) / 2.;}} else for (int j=0; j<n; ++j) {int l = min(max(x2[j], a), max(x2[j+1], a)), r = max(min(x2[j], b), min(x2[j+1], b));if (l == r) {if (x2[j] == l) p[c].x = x2[j], p[c].z = z2[j],p[c++].y = interp(x1[i], y1[i], x1[i+1], y1[i+1], x2[j]);} else if (l < r) {if (x2[j] > x2[j+1]) r = l+r, l = r-l, r = r-l;if (x2[j+1] != l) p[c].x = l, p[c].y = interp(x1[i], y1[i], x1[i+1], y1[i+1], l),p[c++].z = interp(x2[j], z2[j], x2[j+1], z2[j+1], l);if (x2[j+1] != r) p[c].x = r, p[c].y = interp(x1[i], y1[i], x1[i+1], y1[i+1], r),p[c++].z = interp(x2[j], z2[j], x2[j+1], z2[j+1], r);}}if (c > 2) s[t] = Area2(p, c), q[t++] = p[0];}for (int i=0; i<n; ++i) {int a = min(x2[i], x2[i+1]), b = max(x2[i], x2[i+1]), c = 0;if (a == b) {for (int j=0; j<m; ++j) {int l = min(x1[j], x1[j+1]), r = max(x1[j], x1[j+1]);if (a < l || a > r) continue;if (a == x1[j]) p[c].x = a, p[c].y = y1[j], p[c++].z = z2[i];else if (a != x1[j+1])p[c].x = a, p[c].y = interp(x1[j], y1[j], x1[j+1], y1[j+1], a), p[c++].z = z2[i];}if (c == 2) {if (find(Point3(a, (p[0].y + p[1].y) / 2., (z2[i] + z2[i+1]) / 2.))) continue;p[2].x = p[3].x = a; p[2].y = p[1].y; p[2].z = p[3].z = z2[i+1]; p[3].y = p[0].y; c = 4;}} else for (int j=0; j<m; ++j) {int l = min(max(x1[j], a), max(x1[j+1], a)), r = max(min(x1[j], b), min(x1[j+1], b));if (l == r) {if (x1[j] == l) p[c].x = x1[j], p[c].y = y1[j],p[c++].z = interp(x2[i], z2[i], x2[i+1], z2[i+1], x1[j]);} else if (l < r) {if (x1[j] > x1[j+1]) r = l+r, l = r-l, r = r-l;if (x1[j+1] != l) p[c].x = l, p[c].y = interp(x1[j], y1[j], x1[j+1], y1[j+1], l),p[c++].z = interp(x2[i], z2[i], x2[i+1], z2[i+1], l);if (x1[j+1] != r) p[c].x = r, p[c].y = interp(x1[j], y1[j], x1[j+1], y1[j+1], r),p[c++].z = interp(x2[i], z2[i], x2[i+1], z2[i+1], r);}}if (c > 2) s[t] = Area2(p, c), q[t++] = p[0];}double ans = 0.;for (int i=1; i<t; ++i) ans += abs(Dot(s[i], q[i]-q[0]));return ans / 6.;
}int main() {ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout << fixed << setprecision(4);while (cin >> m >> n && m) cout << solve() << endl;return 0;
}优化版:
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;#define eps 1e-10
#define N 105
double s[N<<1]; int x1[N], _y[N], x2[N], z2[N]; int m, n, t, e;
struct Point {double x, y;Point(double x = 0., double y = 0.): x(x), y(y) {}
} p[N];
struct Point3 {double x, y, z;Point3(double x = 0., double y = 0., double z = 0.): x(x), y(y), z(z) {}void Normalize() {double l = sqrt(x*x + y*y + z*z); x /= l; y /= l; z /= l;}
} q[N<<1], v[N<<1], f[N];
typedef Point3 Vector3;Vector3 operator+ (const Vector3& A, const Vector3& B) {return Vector3(A.x + B.x, A.y + B.y, A.z + B.z);
}Vector3 operator- (const Vector3& A, const Vector3& B) {return Vector3(A.x - B.x, A.y - B.y, A.z - B.z);
}int dcmp(double x) {return abs(x) < eps ? 0 : (x < 0. ? -1 : 1);
}bool operator== (const Point3& a, const Point3& b) {return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0 && dcmp(a.z - b.z) == 0;
}double Dot(const Vector3& A, const Vector3& B) {return A.x * B.x + A.y * B.y + A.z * B.z;
}Vector3 Cross(const Vector3& A, const Vector3& B) {return Vector3(A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
}double Area2(const Point* p, int n) {double area = p[0].y * (p[n-1].x - p[1].x) + p[n-1].y * (p[n-2].x - p[0].x);for (int i=n-2; i>0; --i) area += p[i].y * (p[i-1].x - p[i+1].x);return area;
}double interp(int x1, int y1, int x2, int y2, double x) {return ((x-x1)*y2 + (x2-x)*y1) / (x2-x1);
}bool find(const Point3& p) {for (int i=0; i<e; ++i) if (f[i] == p) return true;return false;
}double solve() {for (int i=0; i<m; ++i) cin >> x1[i] >> _y[i];for (int i=0; i<n; ++i) cin >> x2[i] >> z2[i];x1[m] = x1[0]; _y[m] = _y[0]; x2[n] = x2[0]; z2[n] = z2[0];for (int i=t=e=0; i<m; ++i) {int a = min(x1[i], x1[i+1]), b = max(x1[i], x1[i+1]), c = 0;if (a != b) {for (int j=0; j<n; ++j) {int l = min(max(x2[j], a), max(x2[j+1], a)), r = max(min(x2[j], b), min(x2[j+1], b));if (l == r) {if (x2[j] == l) p[c].x = x2[j], p[c++].y = z2[j];} else if (l < r) {if (x2[j] > x2[j+1]) r = l+r, l = r-l, r = r-l;if (x2[j+1] != l) p[c].x = l, p[c++].y = interp(x2[j], z2[j], x2[j+1], z2[j+1], l);if (x2[j+1] != r) p[c].x = r, p[c++].y = interp(x2[j], z2[j], x2[j+1], z2[j+1], r);}}if (c > 2) {int dx = x1[i+1] - x1[i], dy = _y[i+1] - _y[i];s[t] = Area2(p, c) * sqrt(dx*dx + dy*dy) / abs(dx);q[t] = Point3(p[0].x, interp(x1[i], _y[i], x1[i+1], _y[i+1], p[0].x), p[0].y);Point3 p1(p[1].x, interp(x1[i], _y[i], x1[i+1], _y[i+1], p[1].x), p[1].y);Point3 p2(p[2].x, interp(x1[i], _y[i], x1[i+1], _y[i+1], p[2].x), p[2].y);v[t] = Cross(p1 - q[t], p2 - p1); v[t++].Normalize();}} else {for (int j=0; j<n; ++j) {int l = min(x2[j], x2[j+1]), r = max(x2[j], x2[j+1]);if (a < l || a > r) continue;if (a == x2[j]) p[c].x = a, p[c++].y = z2[j];else if (a != x2[j+1]) p[c].x = a, p[c++].y = interp(x2[j], z2[j], x2[j+1], z2[j+1], a);}if (c == 2) {f[e].x = a; f[e].y = (_y[i] + _y[i+1]) / 2.; f[e++].z = (p[0].y + p[1].y) / 2.;p[2].x = p[3].x = a; p[2].y = p[1].y; p[3].y = p[0].y; c = 4;v[t].x = 1.; v[t].y = 0.; v[t].z = 0.; q[t].x = a; q[t].y = _y[i]; q[t].z = p[0].y;s[t++] = 2 * abs((p[0].y - p[1].y) * (_y[i] - _y[i+1]));}}}for (int i=0; i<n; ++i) {int a = min(x2[i], x2[i+1]), b = max(x2[i], x2[i+1]), c = 0;if (a != b) {for (int j=0; j<m; ++j) {int l = min(max(x1[j], a), max(x1[j+1], a)), r = max(min(x1[j], b), min(x1[j+1], b));if (l == r) {if (x1[j] == l) p[c].x = x1[j], p[c++].y = _y[j];} else if (l < r) {if (x1[j] > x1[j+1]) r = l+r, l = r-l, r = r-l;if (x1[j+1] != l) p[c].x = l, p[c++].y = interp(x1[j], _y[j], x1[j+1], _y[j+1], l);if (x1[j+1] != r) p[c].x = r, p[c++].y = interp(x1[j], _y[j], x1[j+1], _y[j+1], r);}}if (c > 2) {int dx = x2[i+1] - x2[i], dz = z2[i+1] - z2[i];s[t] = Area2(p, c) * sqrt(dx*dx + dz*dz) / abs(dx);q[t] = Point3(p[0].x, p[0].y, interp(x2[i], z2[i], x2[i+1], z2[i+1], p[0].x));Point3 p1(p[1].x, p[1].y, interp(x2[i], z2[i], x2[i+1], z2[i+1], p[1].x));Point3 p2(p[2].x, p[2].y, interp(x2[i], z2[i], x2[i+1], z2[i+1], p[2].x));v[t] = Cross(p1 - q[t], p2 - p1); v[t++].Normalize();}} else {for (int j=0; j<m; ++j) {int l = min(x1[j], x1[j+1]), r = max(x1[j], x1[j+1]);if (a < l || a > r) continue;if (a == x1[j]) p[c].x = a, p[c++].y = _y[j];else if (a != x1[j+1]) p[c].x = a, p[c++].y = interp(x1[j], _y[j], x1[j+1], _y[j+1], a);}if (c == 2) {f[e].x = a; f[e].y = (p[0].y + p[1].y) / 2.; f[e].z = (z2[i] + z2[i+1]) / 2.;if (find(f[e])) continue;p[2].x = p[3].x = a; p[2].y = p[1].y; p[3].y = p[0].y; c = 4;v[t].x = 1.; v[t].y = 0.; v[t].z = 0.; q[t].x = a; q[t].y = p[0].y; q[t].z = z2[i];s[t++] = 2 * abs((p[0].y - p[1].y) * (z2[i] - z2[i+1])); ++e;}}}double ans = 0.;for (int i=1; i<t; ++i) ans += abs(s[i] * Dot(v[i], q[i]-q[0]));return ans / 6.;
}int main() {ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout << fixed << setprecision(4);while (cin >> m >> n && m) cout << solve() << endl;return 0;
}