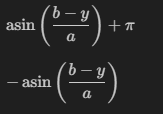【机器学习300问】56、什么是自编码器？

一、什么是自编码器？

自编码器（Autoencoder，AE）本质是一种特殊的神经网络架构。主要用于无监督学习和特征学习任务。它的目标是通过编码然后解码的过程，学会重构其输入数据，试图还原其原始输入的。

当时我学到这里，我是一头雾水！为什么这样子做？AE他想把输出数据原原本本的还原成输入的数据，费那么多功夫干吗，不做这个编码和解码操作，输入数据不就等于输出数据了吗？但其实不然，这里面大有学问，下面我用一个例子给大家解释一下。

（1）一个例子让你深刻理解什么是自编码器！

读书的时候都听过这么一句话吧？话是这么说的“要先把书读薄，然后再把书读厚”。没错！这就是自编码器的精髓！他就是模仿了这样一个过程。

把书读薄：对应自编码器编码过程。编码器接收原始高维数据（比如一个长文档或一张高清图像），并将其压缩为一个低维的隐藏表示（隐藏层的输出）。这个隐藏层就像是对整本书内容的高度浓缩，就好比把一本厚厚的书提炼出了其中的要点和关键信息，形成了“薄书”。
把书读厚：对应自编码器解码过程。解码器利用这个低维隐藏表示尝试重构原始数据，尽可能接近输入数据本身。尽管隐藏层的信息量相对较小，但解码器通过学习能够基于这些少量信息还原出较丰富的内容，就像基于“薄书”的要点重新扩展成了一本包含大部分原意内容的“厚书”。

二、自编码器长什么样？

（1）主要组成部分

编码器（Encoder）：这是一个前向传播网络，负责将输入数据映射到一个低维的潜在空间。编码器将高维的原始数据压缩成一个低维的编码或隐含向量，这个向量往往比原始数据维度小很多，但力求保留最重要的特征。这就像你准备将图画简化成黑白线条草图，需要确定最重要的轮廓和特征来描绘。
隐藏层：这是编码过程的中间产物，它是对输入数据的高度抽象和压缩版本。在这一层，数据被强制简化为最重要的特征子集。
解码器（Decoder）：与编码器相反，解码器是一个从低维潜在空间到原始数据空间的逆映射网络。它的任务是根据编码后的低维向量尽可能准确地重构原始输入数据。这等同于你用那个草图尝试再现原画的细节，尽管颜色丢失了，但我们希望图案仍旧是清晰的。

（2）直观感受

① 简单的两层自编码器

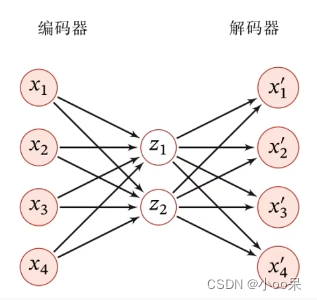
② 自编码器的架构表示

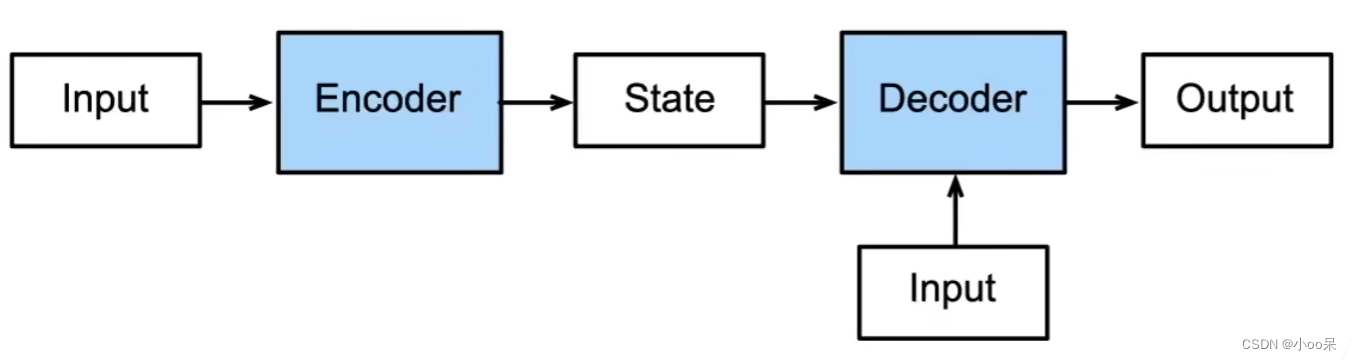
编码器处理输入，解码器处理输出。

③ RNN中的自编码器结构

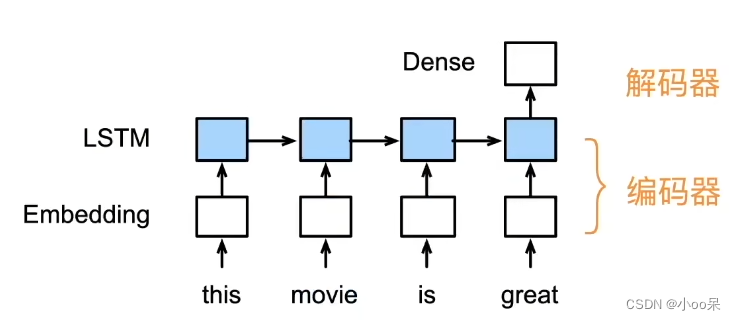
④ CNN中的自编码器结构

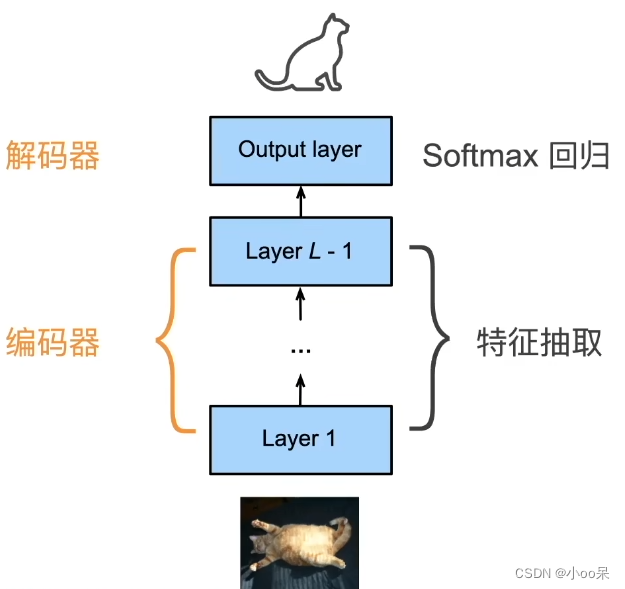
三、自编码器的目标是什么？

自编码器的目标是学习如何有效地对输入数据进行编码和解码，使得通过自编码器的输出（即解码后的数据）能够尽可能地接近原始输入数据。这个过程可以理解为，自编码器尝试学习，如何精准地复制或重建其输入。其根本目的是探索数据中的关键特征并保留这些信息。

让我通过一个小例子来深入揭示自编码器的目标是什么？

假设你有一张彩色风景照片，这张照片包含了丰富的颜色信息以及各种细节纹理。现在，你的目标是仅使用黑白两色重新手绘出一幅画面，不仅要保留风景的主要特征和结构，还要尽量做到即使没有原始的色彩信息，观众也能识别出那是一幅风景画。

编码过程：你的大脑开始分析这张照片，试图理解其核心元素和重要的特征。就像编码器将高维的输入数据映射到一个低维的“隐藏”空间（潜在表示）。你会观察原始的彩色照片，并从中抽取出重要的信息，决定了哪些是你要在画作中体现出来的元素——比如，山的轮廓，树的分布，河流的蜿蜒等等。

压缩过程：这个低维的潜在表示就像是一种抽象的“草图”，它仅包含有限的信息量，但理论上应该蕴含了重构原始图像所必需的核心特征。

解码过程：你用黑白颜色开始创作，试图利用这些简单的线条和形状来重建原始的彩色风景。这相当于解码器的工作，它接收低维的隐藏表示，然后尝试重建数据，即在画布上用黑白色反映出原始的风景。虽然最终的画不可能包含彩色照片中的所有细节和色彩（因为材料和信息已经有所简化），但目标是尽量让重建的风景与原始照片保持核心特征和整体结构的一致。

自编码器的目标就是在简化后的数据表示上进行学习，使得经过解码之后，能够最大化地复原原始数据的关键特性。在这个画风景的比喻中，尽管色彩和一些细节无法复原，但如果最终的黑白画仍能让人一眼看出原始风景的美丽，那么你就实现了自编码器的目标——用一个更简洁的形式捕捉和表达了原始数据的精髓。

四、自编码器的目标函数是什么

自编码器的目标函数通常是指重构损失函数，其目的是让经过编码和解码后的输出尽可能接近原始输入。具体来说，自编码器试图学习一个编码函数 $f_{encoder}$ 将输入数据 $x$ 映射到一个潜在空间的低纬编码 $z=f_\Phi (x)$ ，然后通过解码函数 $f_{decoder}$ 将 $z$ 再映射回原始数据的近似版本 $\hat x=f_\Theta (x)$