例题一

解法(归并排序):
算法思路:
归并排序的流程充分的体现了「分⽽治之」的思想,⼤体过程分为两步:
◦ 分:将数组⼀分为⼆为两部分,⼀直分解到数组的⻓度为 1 ,使整个数组的排序过程被分为
「左半部分排序」 + 「右半部分排序」;
◦ 治:将两个较短的「有序数组合并成⼀个⻓的有序数组」,⼀直合并到最初的⻓度。
例题二

解法(利⽤归并排序的过程 --- 分治):
算法思路:
⽤归并排序求逆序数是很经典的⽅法,主要就是在归并排序的合并过程中统计出逆序对的数量,也
就是在合并两个有序序列的过程中,能够快速求出逆序对的数量。
我们将这个问题分解成⼏个⼩问题,逐⼀破解这道题。
注意:默认都是升序,如果掌握升序的话,降序的归并过程也是可以解决问题的。
• 先解决第⼀个问题,为什么可以利⽤归并排序?
如果我们将数组从中间划分成两个部分,那么我们可以将逆序对产⽣的⽅式划分成三组:
• 逆序对中两个元素:全部从左数组中选择
• 逆序对中两个元素:全部从右数组中选择
• 逆序对中两个元素:⼀个选左数组另⼀个选右数组
根据排列组合的分类相加原理,三种种情况下产⽣的逆序对的总和,正好等于总的逆序对数量。
⽽这个思路正好匹配归并排序的过程:
• 先排序左数组;
• 再排序右数组;
• 左数组和右数组合⼆为⼀。
因此,我们可以利⽤归并排序的过程,先求出左半数组中逆序对的数量,再求出右半数组中逆序对的数量,最后求出⼀个选择左边,另⼀个选择右边情况下逆序对的数量,三者相加即可。
• 解决第⼆个问题,为什么要这么做?
在归并排序合并的过程中,我们得到的是两个有序的数组。我们是可以利⽤数组的有序性,快速统计出逆序对的数量,⽽不是将所有情况都枚举出来。
• 最核⼼的问题,如何在合并两个有序数组的过程中,统计出逆序对的数量?
合并两个有序序列时求逆序对的⽅法有两种:
1. 快速统计出某个数前⾯有多少个数⽐它⼤;
2. 快速统计出某个数后⾯有多少个数⽐它⼩;
⽅法⼀:快速统计出某个数前⾯有多少个数⽐它⼤
通过⼀个⽰例来演⽰⽅法⼀:
假定已经有两个已经有序的序列以及辅助数组 left = [5, 7, 9] right = [4, 5, 8] help = [ ],通过合并两
个有序数组的过程,来求得逆序对的数量:
规定如下定义来叙述过程:
cur1 遍历 left 数组,cur2 遍历 right 数组
ret 记录逆序对的数量
第⼀轮循环:
left[cur1] > right[cur2],由于两个数组都是升序的,那么我们可以断定,此刻 left 数组中 [cur1, 2] 区间内的 3 个元素均可与 right[cur2] 的元素构成逆序对,因此可以累加逆序对的数量 ret += 3,并且将 right[cur2] 加⼊到辅助数组中,cur2++ 遍历下⼀个元素。
第⼀轮循环结束后:left = [5, 7, 9] right = [x, 5, 8] help = [4] ret = 3 cur1 = 0 cur2 = 1
第⼆轮循环: left[cur1] == right[cur2],因为 right[cur2] 可能与 left 数组中往后的元素构成逆序对,因此我 们需要将 left[cur1] 加⼊到辅助数组中去,此时没有产⽣逆序对,不更新 ret。
第⼆轮循环结束后:left = [x, 7, 9] right = [x, 5, 8] help = [4, 5] ret = 3 cur1 = 1 cur2 = 1
第三轮循环: left[cur1] > right[cur2],与第⼀轮循环相同,此刻 left 数组中[cur1, 2] 区间内的 2 个元素均可 与 right[cur2] 的元素构成逆序对,更新 ret 的值为 ret += 2,并且将 right[cur2] 加⼊到辅助数组中 去,cur2++ 遍历下⼀个元素。
第三轮循环结束后:left = [x, 7, 9] right = [x, x, 8] help = [4, 5, 5] ret = 5 cur1 = 1 cur2 = 2
第四轮循环: left[cur1] < right[cur2],由于两个数组都是升序的,因此我们可以确定 left[cur1] ⽐ right 数组中的所有元素都要⼩。left[cur1] 这个元素是不可能与 right 数组中的元素构成逆序对。因此,⼤胆的将 left[cur1] 这个元素加⼊到辅助数组中去,不更细 ret 的值。
第四轮循环结束后:left = [x, x, 9] right = [x, x, 8] help = [4, 5, 5, 7] ret = 5 cur1 = 2 cur2 = 2
第五轮循环:left[cur1] > right[cur2],与第⼀、第三轮循环相同。此时 left 数组内的 1 个元素能与
right[cur2] 构成逆序对,更新 ret 的值,并且将 right[cur2] 加⼊到辅助数组中去。
第五轮循环结束后:left = [x, x, 9] right = [x, x, x] help = [4, 5, 5, 7, 8] ret = 6 cur1 = 2 cur2 = 2
处理剩余元素:
• 如果是左边出现剩余,说明左边剩下的所有元素都是⽐右边元素⼤的,但是它们都是已经被计算过的(我们以右边的元素为基准的),因此不会产⽣逆序对,仅需归并排序即可。
• 如果是右边出现剩余,说明右边剩下的元素都是⽐左边⼤的,不符合逆序对的定义,因此也不需要 处理,仅需归并排序即可。
整个过程只需将两个数组遍历⼀遍即可,时间复杂度为 O(N)。
由上述过程我们可以得出⽅法⼀统计逆序对的关键点:
在合并有序数组的时候,遇到左数组当前元素 > 右数组当前元素时,我们可以通过计算左数组中剩余元素的⻓度,就可快速求出右数组当前元素前⾯有多少个数⽐它⼤,对⽐解法⼀中⼀个⼀个枚举逆序对效率快了许多。
⽅法⼆:快速统计出某个数后⾯有多少个数⽐它⼩
依旧通过⼀个⽰例来演⽰⽅法⼆:
假定已经有两个已经有序的序列以及辅助数组 left = [5, 7, 9] right = [4, 5, 8] help = [ ],通过合并两
个有序数组的过程,来求得逆序对的数量:
规定如下定义来叙述过程:
cur1 遍历 left 数组,cur2 遍历 right 数组 ret 记录逆序对的数量
第⼀轮循环: left[cur1] > right[cur2],先不要着急统计,因为我们要找的是当前元素后⾯有多少⽐它⼩的,这⾥虽然出现了⼀个,但是 right 数组中依旧还可能有其余⽐它⼩的。因此此时仅将 right[cur2] 加⼊到辅助数组中去,并且将 cur2++。
第⼀轮循环结束后:left = [5, 7, 9] right = [x, 5, 8] help = [4] ret = 0 cur1 = 0 cur2 = 1 第⼆轮循环:
left[cur1] == right[cur2],由于两个数组都是升序,这个时候对于元素 left[cur1] 来说,我们已
经可以断定 right 数组中 [0, cur2) 左闭右开区间上的元素都是⽐它⼩的。因此此时可以统计逆序对的数量 ret += cur2 - 0,并且将 left[cur1] 放⼊到辅助数组中去,cur1++ 遍历下⼀个元素。
第⼆轮循环结束后:left = [x, 7, 9] right = [x, 5, 8] help = [4, 5] ret = 1 cur1 = 1 cur2 = 1
第三轮循环:left[cur1] > right[cur2],与第⼀轮循环相同,直接将 right[cur2] 加⼊到辅助数组中去,cur2++ 遍历下⼀个元素。
第三轮循环结束后:left = [x, 7, 9] right = [x, x, 8] help = [4, 5, 5] ret = 1 cur1 = 1 cur2 = 2
第四轮循环:left[cur1] < right[cur2],由于两个数组都是升序的,这个时候对于元素 left[cur1] 来说,我们依旧已经可以断定 right 数组中 [0, cur2) 左闭右开区间上的元素都是⽐它⼩的。因此此时可以统计逆序对的数量 ret += cur2 - 0,并且将 left[cur1] 放⼊到辅助数组中去,cur1++ 遍历下⼀个元素。
第四轮循环结束后:left = [9] right = [8] help = [4, 5, 5, 7] ret = 3 cur1 = 2 cur2 = 2
第五轮循环:left[cur1] > right[cur2],与第⼀、第三轮循环相同。直接将 right[cur2] 加⼊到辅助数组中去,cur2++ 遍历下⼀个元素。
第五轮循环结束后:left = [x, x, 9] right = [x, x, x] help = [4, 5, 5, 7, 8] ret = 3 cur1 = 2 cur2 = 2
处理剩余元素:
• 如果是左边出现剩余,说明左边剩下的所有元素都是⽐右边元素⼤的,但是相⽐较于⽅法⼀,逆序对的数量是没有统计过的。因此,我们需要统计 ret 的值:
◦ 设左边数组剩余元素的个数为 leave
◦ ret += leave * (cur2 - 0) 对于本题来说,处理剩余元素的时候, left 数组剩余 1 个元素,cur2 - 0 = 3,因此 ret 需要类加上 3,结果为 6。与⽅法⼀求得的结果相同。
• 如果是右边出现剩余,说明右边剩下的元素都是⽐左边⼤的,不符合逆序对的定义,因此也不需要处理,仅需归并排序即可。整个过程只需将两个数组遍历⼀遍即可,时间复杂度依旧为 O(N)。
由上述过程我们可以得出⽅法⼆统计逆序对的关键点:
在合并有序数组的时候,遇到左数组当前元素 <= 右数组当前元素时,我们可以通过计算右数组已经遍历过的元素的⻓度,快速求出左数组当前元素后⾯有多少个数⽐它⼤。
但是需要注意的是,在处理剩余元素的时候,⽅法⼆还需要统计逆序对的数量。

例题三

3. 解法(归并排序):
算法思路: 这⼀道题的解法与 求数组中的逆序对 的解法是类似的,但是这⼀道题要求的不是求总的个数,⽽是要返回⼀个数组,记录每⼀个元素的右边有多少个元素⽐⾃⼰⼩。
但是在我们归并排序的过程中,元素的下标是会跟着变化的,因此我们需要⼀个辅助数组,来将数
组元素和对应的下标绑定在⼀起归并,也就是再归并元素的时候,顺势将下标也转移到对应的位置
上。由于我们要快速统计出某⼀个元素后⾯有多少个⽐它⼩的,因此我们可以利⽤求逆序对的第⼆种⽅法。
算法流程:
• 创建两个全局的数组:
vector<int> index:记录下标
vector<int> ret:记录结果
index ⽤来与原数组中对应位置的元素绑定,ret ⽤来记录每个位置统计出来的逆序对的个数。
• countSmaller() 主函数:
a. 计算 nums 数组的⼤⼩为 n;
b. 初始化定义的两个全局的数组;
i. 为两个数组开辟⼤⼩为 n 的空间
ii. index 初始化为数组下标;
iii. ret 初始化为 0
c. 调⽤ mergeSort() 函数,并且返回 ret 结果数组。
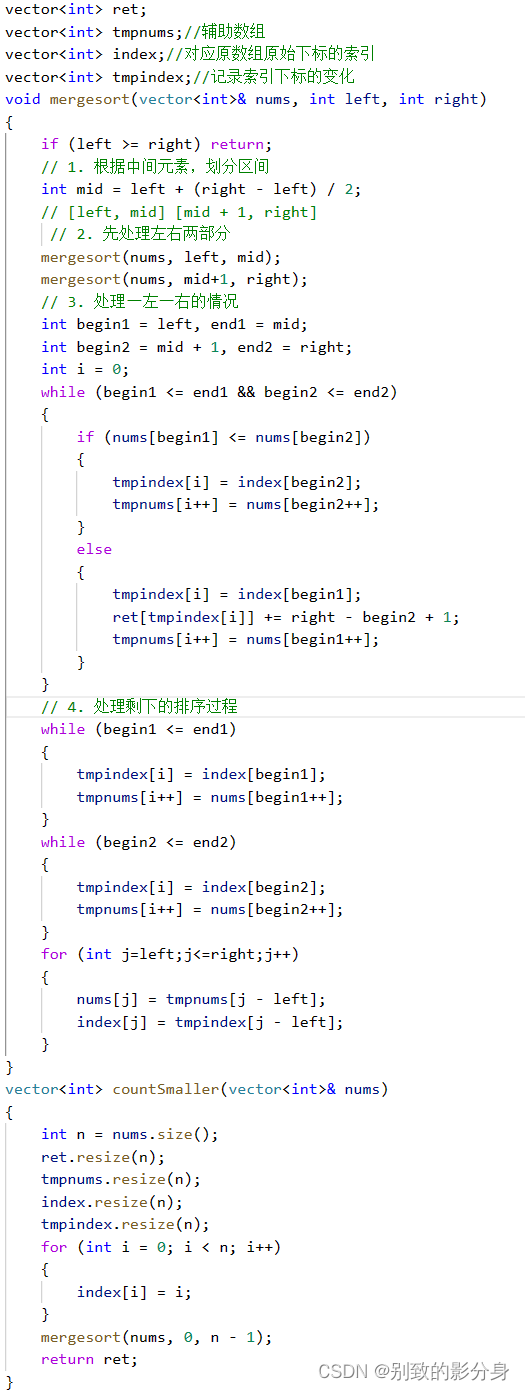
• void mergeSort( vector<int>& nums, int left, int right ) 函数:
函数设计:通过修改全局的数组 ret, 统计出每⼀个位置对应的逆序对的数量,并且排序;
⽆需返回值,因为直接对全局变量修改,当函数结束的时候,全局变量已经被修改成最后的结果。
• mergeSort() 函数流程:
a. 定义递归出⼝:left >= right 时,直接返回;
b. 划分区间:根据中点 mid,将区间划分为 [left, mid] 和 [mid + 1, right];
c. 统计左右两个区间逆序对的数量:
i. 统计左边区间 [left, mid] 中每个元素对应的逆序对的数量到 ret 数组中,并排序;
ii. 统计右边区间 [mid + 1, right] 中每个元素对应的逆序对的数量到 ret 数组中,并排序。 d. 合并左右两个有序区间,并且统计出逆序对的数量:
i. 创建两个⼤⼩为 right - left + 1 ⼤⼩的辅助数组:
• numsTmp: 排序⽤的辅助数组;
• indexTmp:处理下标⽤的辅助数组。
ii. 初始化遍历数组的指针:cur1 = left(遍历左半部分数组)cur2 = mid + 1(遍历右半边数
组)dest = 0(遍历辅助数组)curRet(记录合并时产⽣的逆序对的数量);
iii. 循环合并区间:
• 当 nums[cur1] <= nums[cur2] 时:
◦ 说明此时 [mid + 1, cur2) 之间的元素都是⼩于 nums[cur1] 的,需要累加到 ret 数组的 indext[cur1] 位置上(因为 index 存储的是元素对应位置在原数组中的下标)
◦ 归并排序:不仅要将数据放在对应的位置上,也要将数据对应的坐标也放在对应的位
置上,使数据与原始的下标绑定在⼀起移动。
• 当 nums[cur1] > nums[cur2] 时,⽆需统计,直接归并,注意 index 也要跟着归并。
iv. 处理归并排序中剩余的元素;
• 当左边有剩余的时候,还需要统计逆序对的数量;
• 当右边还有剩余的时候,⽆需统计,直接归并。
v. 将辅助数组的内容替换到原数组中去;
例题四

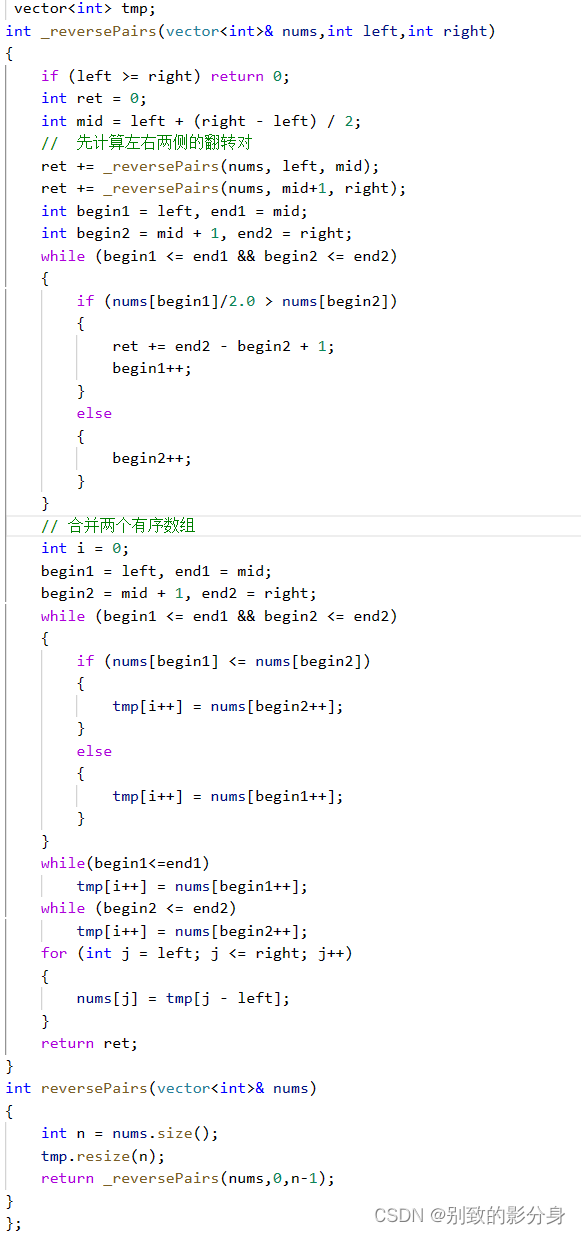
解法(归并排序):
算法思路:
⼤思路与求逆序对的思路⼀样,就是利⽤归并排序的思想,将求整个数组的翻转对的数量,转换成
三部分:左半区间翻转对的数量,右半区间翻转对的数量,⼀左⼀右选择时翻转对的数量。重点就
是在合并区间过程中,如何计算出翻转对的数量。
与上个问题不同的是,上⼀道题我们可以⼀边合并⼀遍计算,但是这道题要求的是左边元素⼤于右
边元素的两倍,如果我们直接合并的话,是⽆法快速计算出翻转对的数量的。
例如 left = [4, 5, 6] right = [3, 4, 5] 时,如果是归并排序的话,我们需要计算 left 数组中有多少个
能与 3 组成翻转对。但是我们要遍历到最后⼀个元素 6 才能确定,时间复杂度较⾼。 因此我们需要在归并排序之前完成翻转对的统计。
下⾯依旧以⼀个⽰例来模仿两个有序序列如何快速求出翻转对的过程:
假定已经有两个已经有序的序列 left = [4, 5, 6] right = [1, 2, 3] 。⽤两个指针 cur1 cur2 遍历两组。
◦ 对于任意给定的 left[cur1] ⽽⾔,我们不断地向右移动 cur2,直到 left[cur1] <= 2 * right[cur2]。此时对于 right 数组⽽⾔,cur2 之前的元素全部都可以与 left[cur1] 构成翻转对。
◦ 随后,我们再将 cur1 向右移动⼀个单位,此时 cur2 指针并不需要回退(因为 left 数组是升序
的)依旧往右移动直到 left[cur1] <= 2 * right[cur2]。不断重复这样的过程,就能够求出所有左右端点分别位于两个⼦数组的翻转对数⽬。
由于两个指针最后都是不回退的的扫描到数组的结尾,因此两个有序序列求出翻转对的时间复杂度
是 O(N)。综上所述,我们可以利⽤归并排序的过程,将求⼀个数组的翻转对转换成求 左数组的翻转对数量 + 右数组中翻转对的数量 + 左右数组合并时翻转对的数量。

![[leetcode] 100. 相同的树](https://img-blog.csdnimg.cn/direct/d4a2bd09cdb9435083092aebe65d1090.png)



![Vue element-plus 导航栏 [el-menu]](https://img-blog.csdnimg.cn/direct/cad688c77fb44593af301196dd40a963.png)