机器学习模型——集成算法

集成学习的定义：

集成学习，顾名思义通过将多个单个学习器集成/组合在一起，使它们共同完成学习任务，以达到提高预测准确率的目的。有时也被称为“多分类器系统 (multi-classifier system)”。

集成学习概述：

集成学习是一种机器学习方法，它通过组合多个弱学习器来形成一个强学习器，以提高预测性能。以下是一些集成学习的关键点：

结合多个学习器：集成学习的核心思想是通过训练多个学习器（基学习器）并结合它们的预测结果来提高整体的预测性能。

适用性广泛：集成学习可以应用于多种机器学习任务，包括分类、回归、特征选择和异常检测等领域。

弱学习器与强学习器：在集成学习中，单个的基学习器通常被称为弱学习器，而通过集成这些弱学习器形成的综合模型则被称为强学习器。

主要算法：集成学习的主要算法包括Bagging、Boosting和Stacking。Bagging通过并行训练多个学习器来减少方差；Boosting通过串行训练学习器来逐步减少偏差；Stacking则是将多个不同的学习器（如KNN、SVM、随机森林等）的输出作为新的特征输入到一个元学习器中进行训练。

集成学习结合策略：

集成学习得到多个学习器后，结合策略得到最终的结果。通常用到最多的是平均法，投票法和学习法。

投票法：

投票法通常用于分类问题。这种技术中使用多个模型来预测每个数据点。每个模型的预测都被视为一次“投票”。大多数模型得到的预测被用作最终预测结果。即对K个学习器的分类结果做一个统计，出现次数最多的类作为预测类。

平均法：

类似于最大投票技术，这里对每个数据点的多次预测进行算数平均。在这种方法中，我们从所有模型中取平均值作为最终预测。平均法可用于在回归问题中进行预测或在计算分类问题的概率时使用。

加权平均法：

这是平均法的扩展。为所有模型分配不同的权重，定义每个模型的预测重要性。

学习法：

为了解决投票法和平均法误差较大的问题。平均法和投票法是对弱学习器的结果做平均或者投票，相对比较简单，但是可能学习误差较大，于是就有了学习法。

对于学习法，代表方法是stacking，当使用stacking的结合策略时，我们不是对弱学习器的结果做简单的逻辑处理，而是再加上一层学习器，也就是说，我们将训练集弱学习器的学习结果作为输入，重新训练一个学习器来得到最终结果。

在这种情况下，我们将弱学习器称为初级学习器，将用于结合的学习器称为次级学习器。对于测试集，我们首先用初级学习器预测一次，得到次级学习器的输入样本，再用次级学习器预测一次，得到最终的预测结果。

集成学习的流程：

集成学习法(Ensemble learning)既可以解决分了问题也可以解决回归问题，但常用于分类。通过将多个分类学习方法聚集在一起来提高分类准确率。

通常一个集成分类器的分类性能会好于单个分类器。集成学习法由训练数据构建一组基分类器(base classifier)，然后通过对每个基分类器的预测进行投票或学习法来进行分类。

在构建分类器的过程中，一般有两种集成方法：

一种是使用训练集的不同子集训练得到不同的基分类器。

另一种方法是使用同一个训练集的不同属性子集训练得到不同的基分类器。

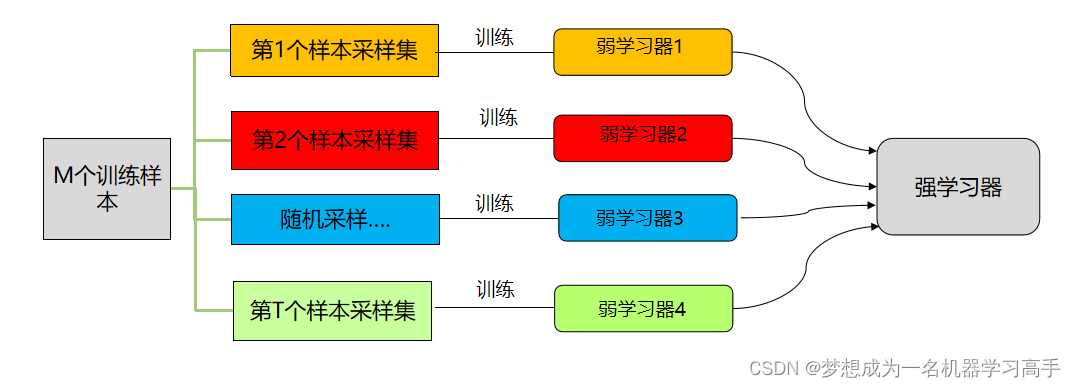
Bagging基本思想：

对训练集有放回地抽取训练样例，从而为每一个基本学习器都构造出一个与训练集相当大小但各不相同的训练集，从而训练出不同的基本学习器；该算法是基于对训练集进行处理的集成方法中最简单、最直观的一种。

Bagging运行原理：

代码实现：

from sklearn.ensemble import BaggingClassifierX = np.array([1,2,3,4,5,6,7,8,9,10])
y = [-1,-1,-1,1,1,1,1,-1,-1,-1,]from sklearn.tree import DecisionTreeClassifierdt = DecisionTreeClassifier(max_depth=1)  # 不设置树深，会让树完全生长，造成过拟合bc = BaggingClassifier(estimator=dt,n_estimators=10)
#                       学习器          迭代次数bc.fit(X.reshape(-1,1),y)
print(bc.score(X.reshape(-1,1),y))