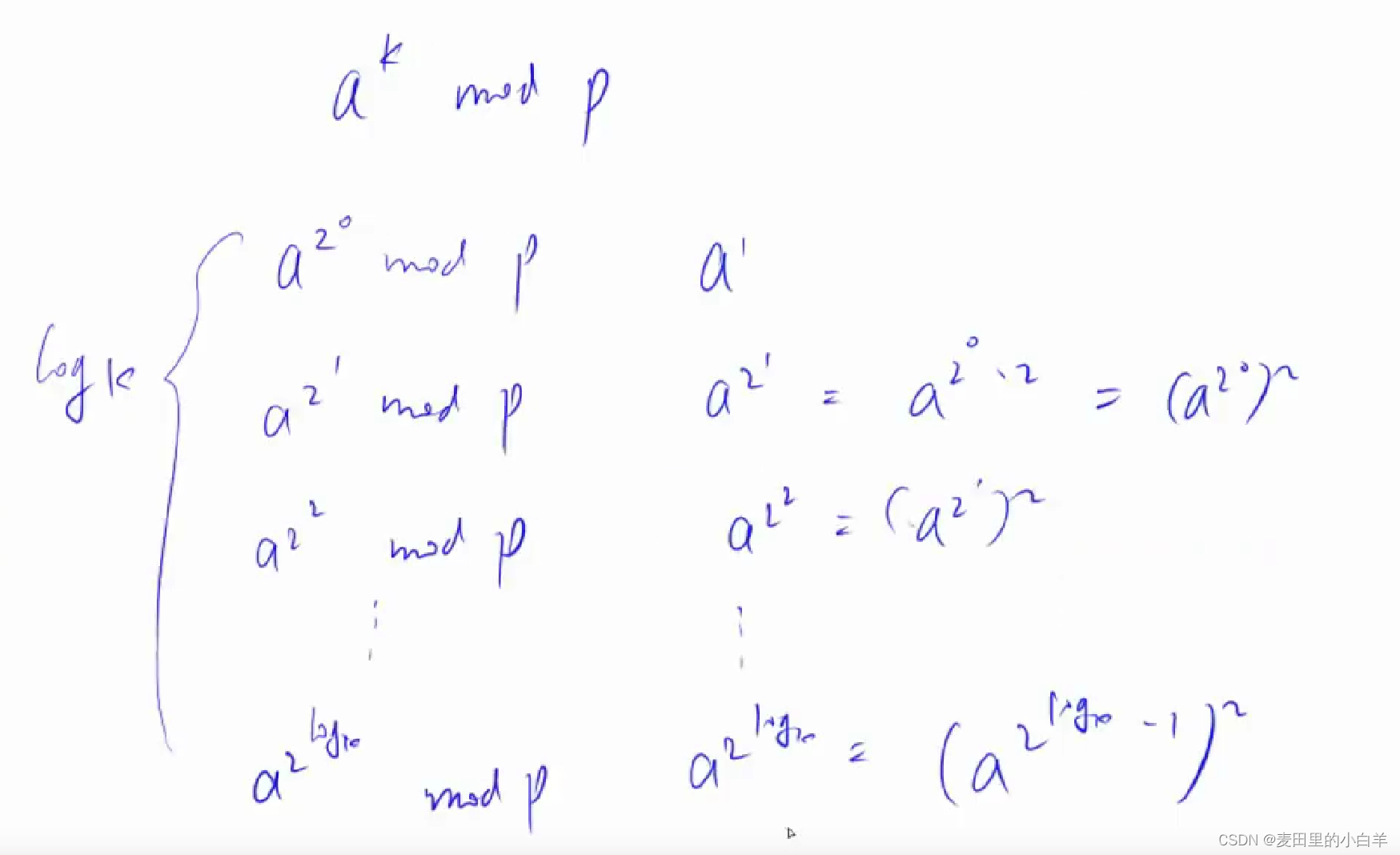题目描述:
给定n组循问,每组询问给定两个整数a,b,请你输出Ca^b mod (1e9+ 7)的值,。
输入格式:
第一行包含整数n。
接下来2行,每行包含一组a和b。
输出格式:
共n行,每行输出一个询问的解。
数据范围:
1≤n<10000
1=b=a=1e5
输入样例:
3
3 1
5 3
2 2输出样例:
3
10
1分析步骤:
第一:大家可以看看我们这道题和 求组合数I的区别。这道题目是不是数据量更大为1e5,如果我们还是用两层for循环的话那么时间复杂度为O(n^2),将要运算的数据为1e10将会超时。所以我们要想一种方法优化。
第二:我们看这道题还是要求Ca^b的答案,还是可以分解为分子是(a!),分母是((a-b)!*b!).所以答案就是分子除以分母。我们还可以这么理解:分子乘上分母的逆元,求逆元的话,我们就可以利用快速幂求解我们的逆元,这样就可以避免TLE(超时)了。
第三:书写主函数,构建整体框架:
-
我们的阶乘和逆元阶乘的初始时都初始化为1
-
利用for循环 来计算我们的正阶乘 和 利用快速幂来计算阶乘的逆元。
-
当我们都初始化完成了之后,就直接输入值利用式子将答案求出来
fact[0] = infact[0] = 1;for(int i = 1 ; i < N ; i ++){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2 , mod) % mod;}第四:书写快速幂:
-
求快速幂就其实相当于将k进行2进制转化
-
我们求的其实是a的2的0次方,a的2的1次方,a的2的2次方... .... .... a的2的log的次方
-
这样的话我们就可以将许多的计算,不断地压缩压缩就可以在有限次就得出答案。
-
if (k & 1) res = (LL)res * a % p;如果k的2进制的最后一位是1的话,我们就将答案乘a
-
a = (LL)a * a % p;将a进行2次方迭代
int qmi(int a, int k, int p) // 求a^k mod p
{int res = 1 ;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
typedef long long LL;
const int N = 100010 , mod = 1e9 + 7;
int fact[N] , infact[N]; // fact求解阶乘,infact求解逆元阶乘int qmi(int a, int k, int p) // 求a^k mod p
{int res = 1 ;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{fact[0] = infact[0] = 1;for(int i = 1 ; i < N ; i ++){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2 , mod) % mod;}int n ;cin>>n;while (n -- ){int a , b ;scanf("%d %d",&a,&b);printf("%d\n", (LL)fact[a]*infact[b] % mod * infact[a - b] % mod);}return 0;
}