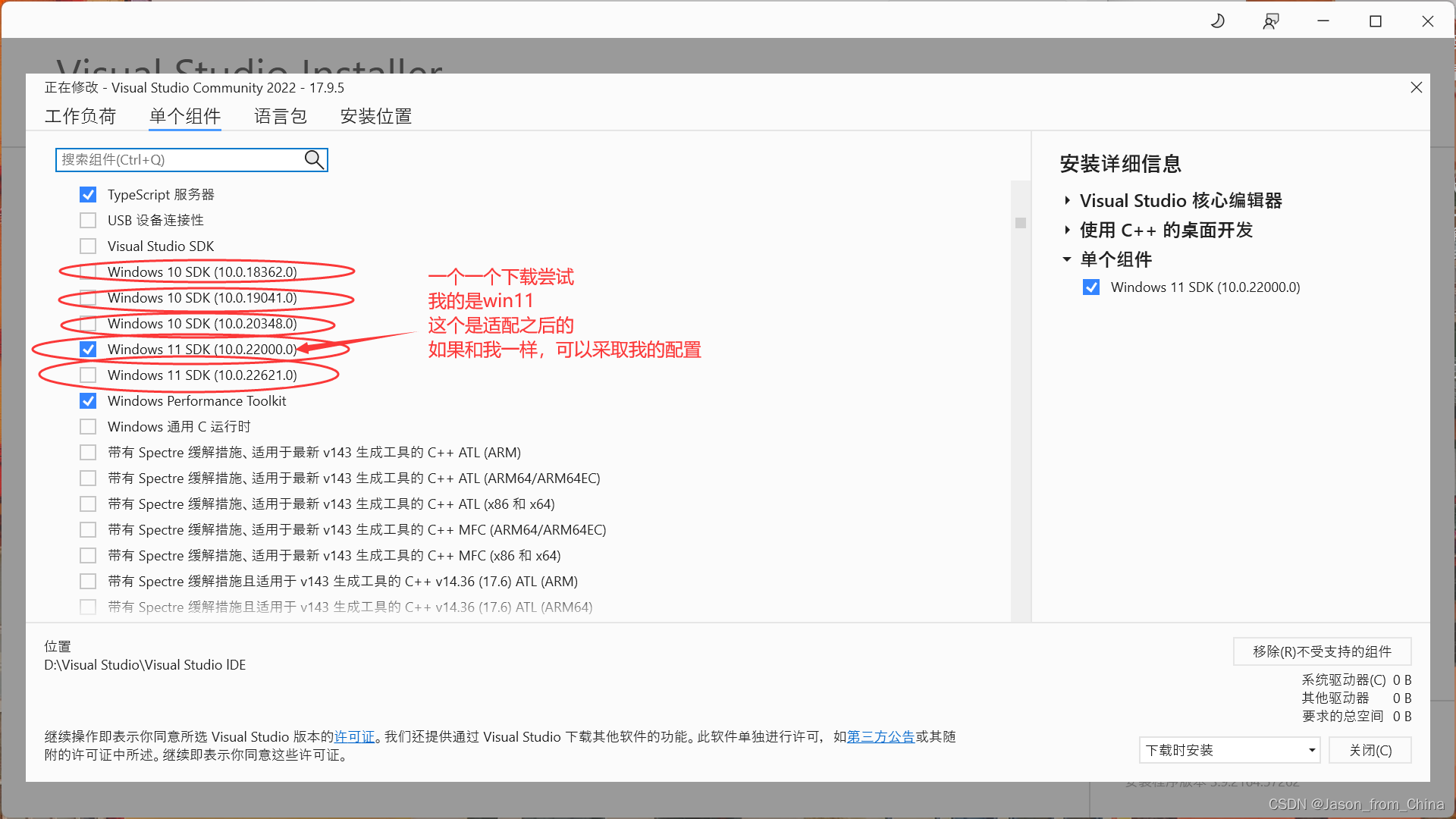
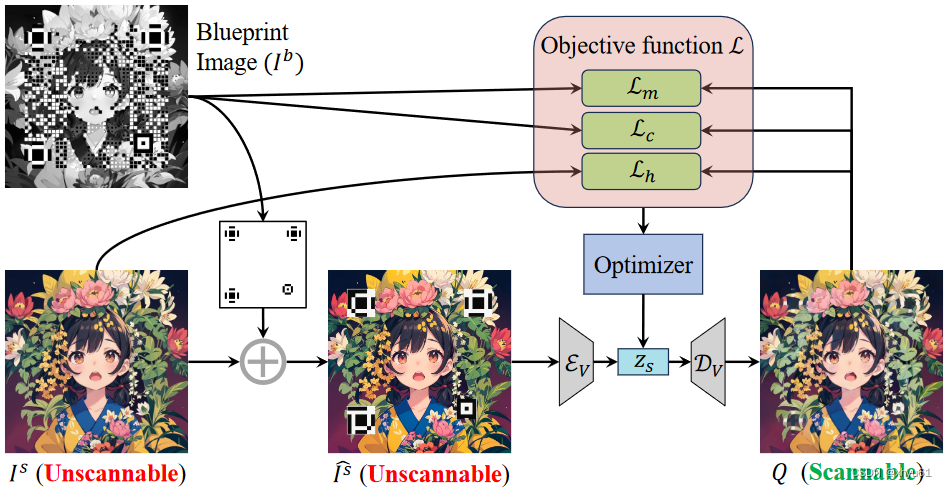
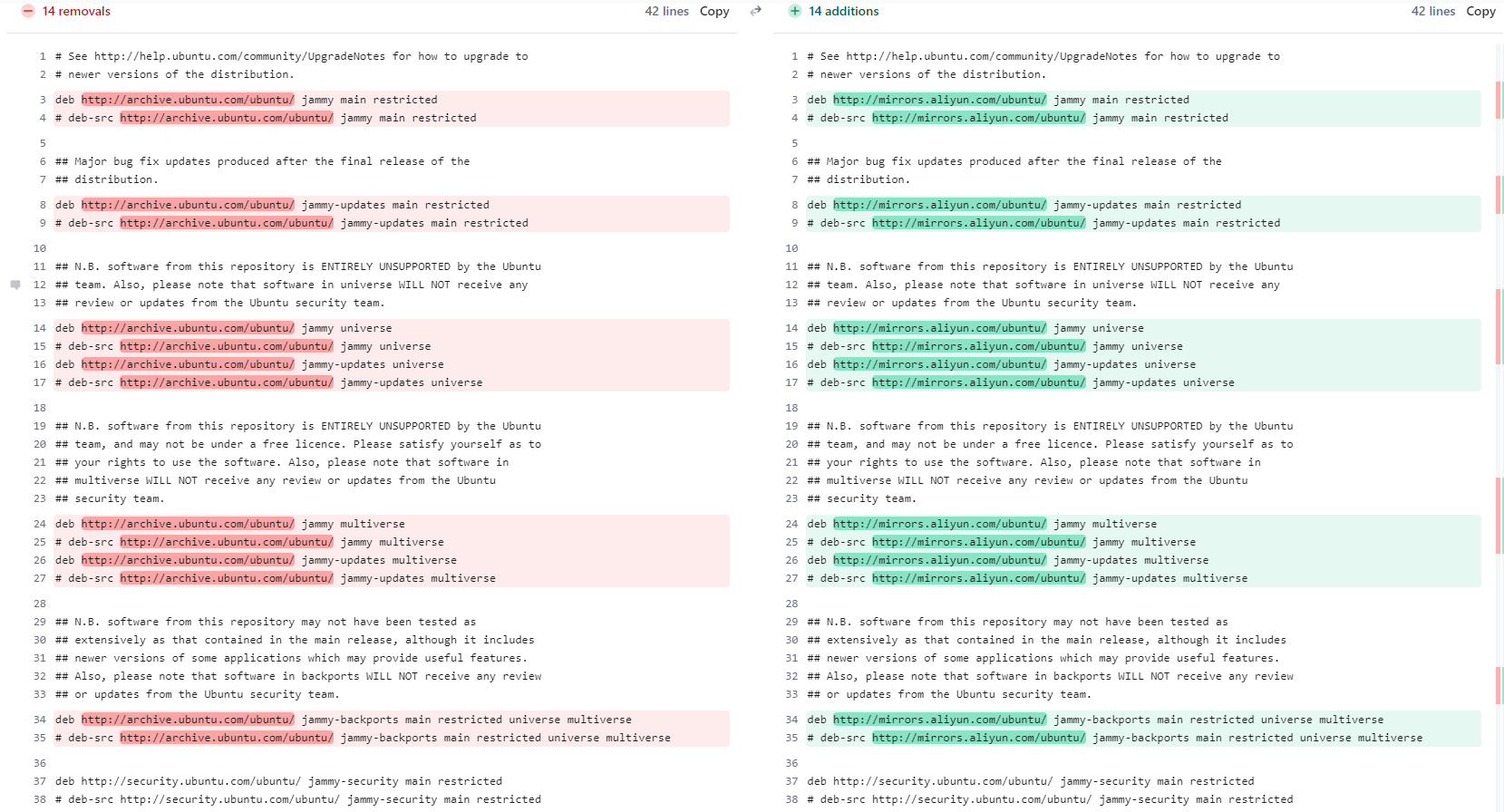
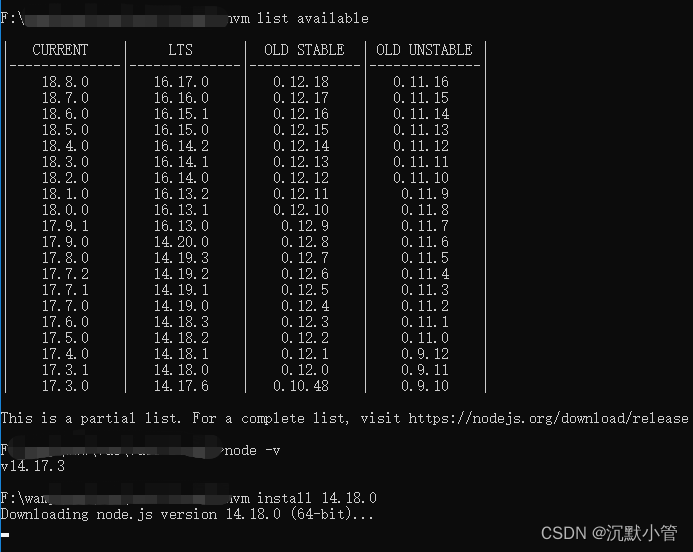
例题一

解法(模拟):
算法思路:
两个链表都是逆序存储数字的,即两个链表的个位数、⼗位数等都已经对应,可以直接相加。
在相加过程中,我们要注意是否产⽣进位,产⽣进位时需要将进位和链表数字⼀同相加。如果产⽣进位的位置在链表尾部,即答案位数⽐原链表位数⻓⼀位,还需要再 new ⼀个结点储存最⾼位。

例题二

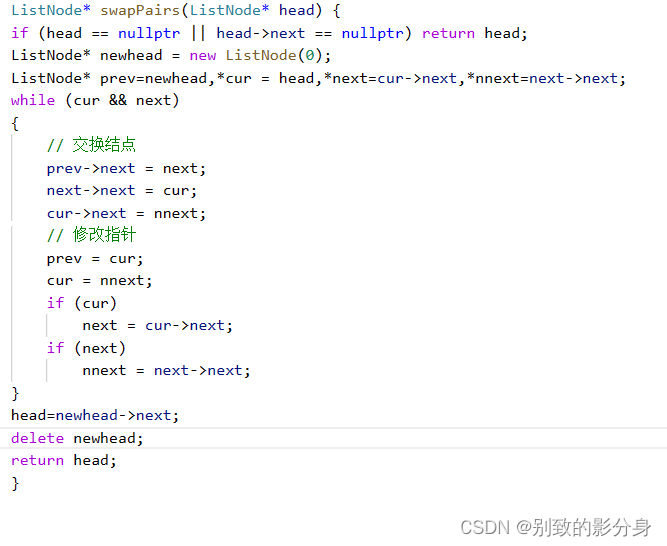
例题三

解法:
算法思路:
画图画图画图,重要的事情说三遍~
1. 找中间节点;
2. 中间部分往后的逆序;
3. 合并两个链表
例题四

解法⼀(利⽤堆):
算法思路:
合并两个有序链表是⽐较简单且做过的,就是⽤双指针依次⽐较链表 1 、链表 2 未排序的最⼩元
素,选择更⼩的那⼀个加⼊有序的答案链表中。 合并 K 个升序链表时,我们依旧可以选择 K 个链表中,头结点值最⼩的那⼀个。那么如何快速的得到头结点最⼩的是哪⼀个呢?⽤堆这个数据结构就好啦~ 我们可以把所有的头结点放进⼀个⼩根堆中,这样就能快速的找到每次 K 个链表中,最⼩的元素是哪个。

解法⼆(递归/分治):
算法思路:
逐⼀⽐较时,答案链表越来越⻓,每个跟它合并的⼩链表的元素都需要⽐较很多次才可以成功排序。⽐如,我们有 8 个链表,每个链表⻓为 100。 逐⼀合并时,我们合并链表的⻓度分别为(0, 100), (100, 100), (200, 100), (300, 100), (400, 100), (500, 100), (600, 100), (700, 100)。所有链表的总⻓度共计 3600。 如果尽可能让⻓度相同的链表进⾏两两合并呢?这时合并链表的⻓度分别是(100, 100) x 4, (200, 200) x 2, (400, 400),共计 2400。⽐上⼀种的计算量整整少了 1/3。
迭代的做法代码细节会稍多⼀些,这⾥给出递归的实现,代码相对简洁,不易写错。
算法流程:
1. 特判,如果题⽬给出空链表,⽆需合并,直接返回;
2. 返回递归结果。
递归函数设计:
1. 递归出⼝:如果当前要合并的链表编号范围左右值相等,⽆需合并,直接返回当前链表;
2. 应⽤⼆分思想,等额划分左右两段需要合并的链表,使这两段合并后的⻓度尽可能相等;
3. 对左右两段分别递归,合并[l, r]范围内的链表;
4. 再调⽤ mergeTwoLists 函数进⾏合并(就是合并两个有序链表)

例题五

解法(模拟):
算法思路:
本题的⽬标⾮常清晰易懂,不涉及复杂的算法,只是实现过程中需要考虑的细节⽐较多。
我们可以把链表按 K 个为⼀组进⾏分组,组内进⾏反转,并且记录反转后的头尾结点,使其可以和前、后连接起来。思路⽐较简单,但是实现起来是⽐较复杂的。我们可以先求出⼀共需要逆序多少组(假设逆序 n 组),然后重复 n 次⻓度为 k 的链表的逆序即可。