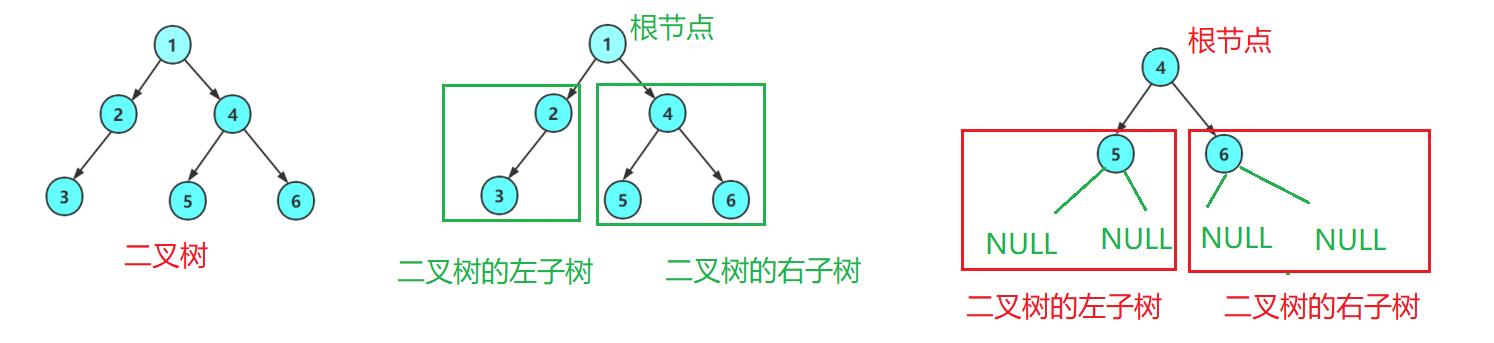
4.二叉树链式结构的实现

二叉树是：

1. 空树

2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

4.1二叉树的遍历

4.2.1 前序、中序以及后序遍历

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

• 也就是先遍历根，再遍历左子树，再遍历右子树

2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

• 也就是先遍历左子树，再遍历根，再遍历右子树

3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

• 也就是先遍历左子树，再遍历右子树，再遍历根

• 由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）**又可解释为根、根的左子树和根的右子树。**NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

二叉树节点的结构

typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

前序遍历

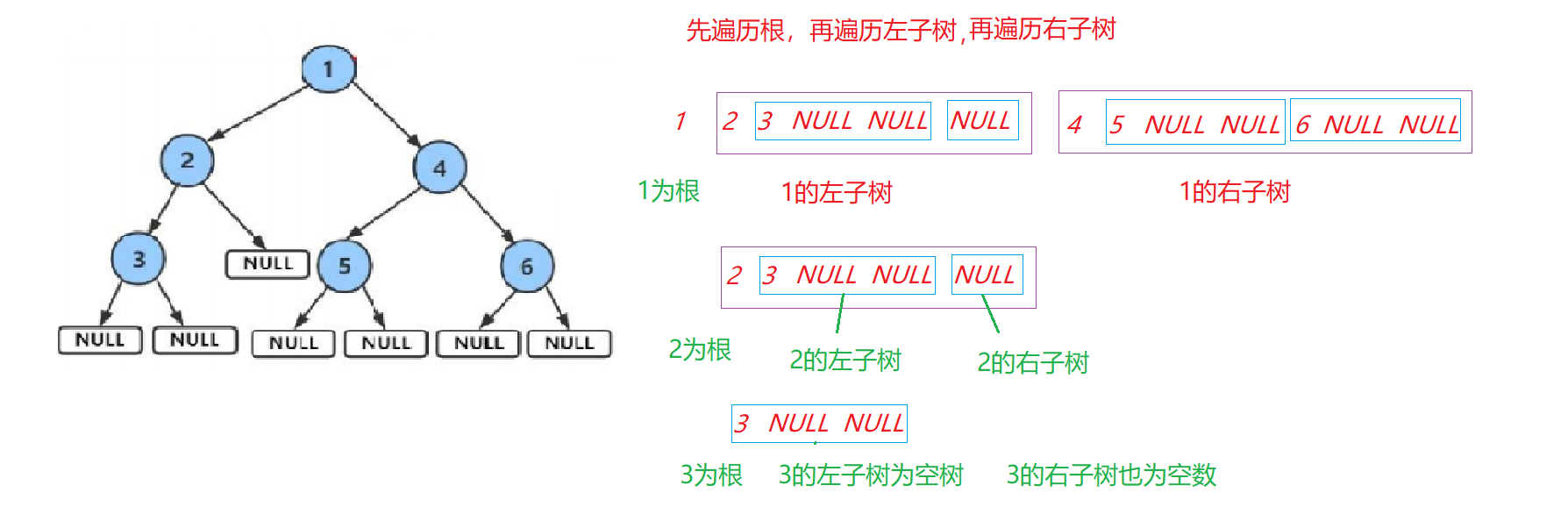
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}// 先遍历根printf("%d ", root->data);// 遍历左子树PreOrder(root->left);// 遍历右子树PreOrder(root->right);
}

中序遍历

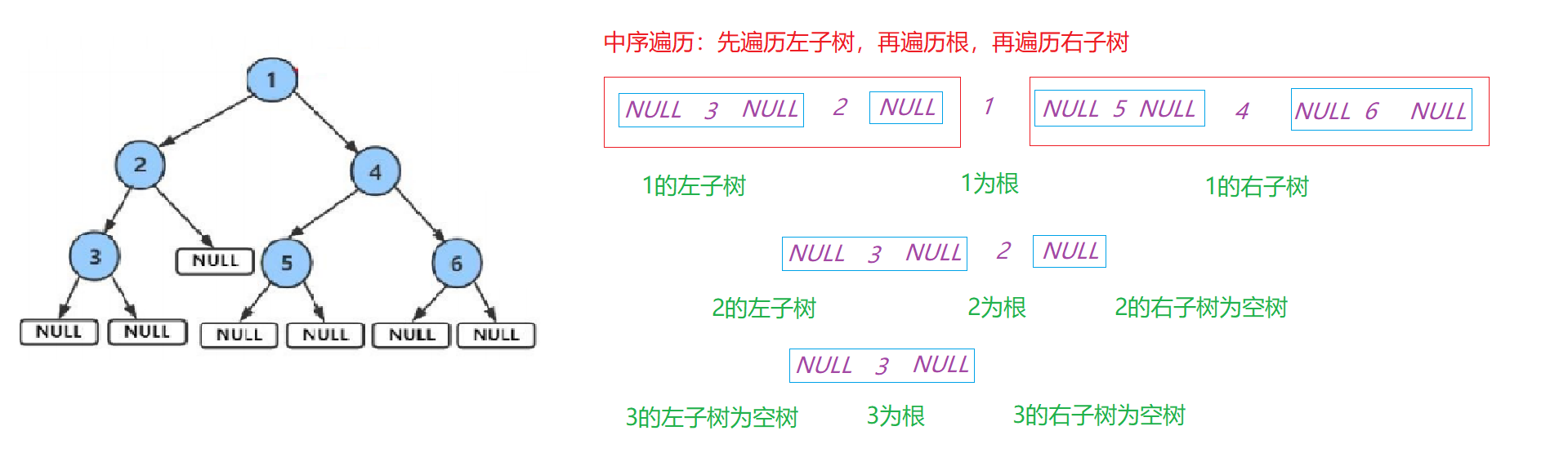
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}// 先遍历左子树InOrder(root->left);// 遍历根printf("%d ", root->data);// 遍历右子树InOrder(root->right);
}

后序遍历

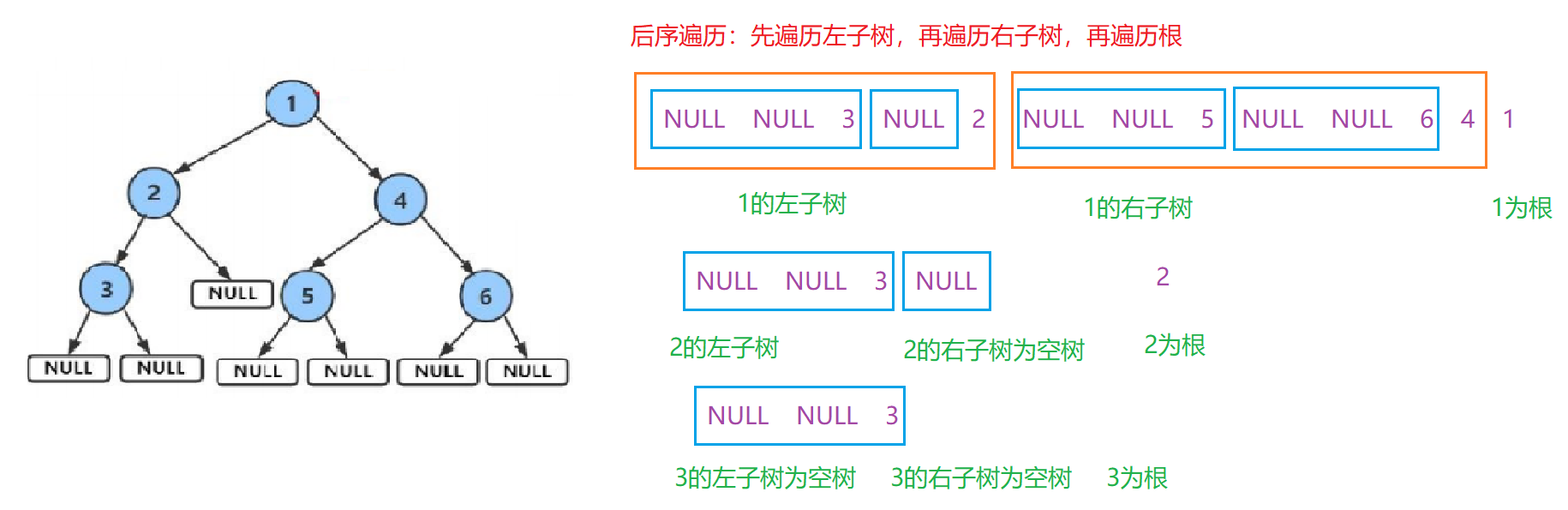
// 二叉树中序遍历
void postOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}// 遍历左子树、遍历右子树、遍历根postOrder(root->left);postOrder(root->right);printf("%d ", root->data);
}

暴力创建一个二叉树（用来验证前序，中序，后序）

#include<stdio.h>
#include<assert.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 通过这个接口来暴力创建二叉树
BTNode* CreateTree()
{BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));assert(n1);BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));assert(n2);BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));assert(n3);BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));assert(n4);BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));assert(n5);BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));assert(n6);n1->data = 1;n2->data = 2;n3->data = 3;n4->data = 4;n5->data = 5;n6->data = 6;// 根节点的左子树n1->left = n2;n2->left = n3;n3->left = NULL;n3->right = NULL;n2->right = NULL;// 根节点的右子树n1->right = n4;n4->left = n5;n5->left = NULL;n5->right = NULL;n4->right = n6;n6->left = NULL;n6->right = NULL;return n1;
}// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}// 二叉树中序遍历
void postOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}postOrder(root->left);postOrder(root->right);printf("%d ", root->data);
}int main()
{BTNode* root = CreateTree();preOrder(root);printf("\n");//InOrder(root);//printf("\n");//postOrder(root);//printf("\n");return 0;
}

4.2.2二叉树所有节点的个数

// 注：可以将求整个二叉树的节点，看作是求
//     左子树的节点           + 右子树的节点            + 1(1为根节点的个数)
//     TreeSize(root->left) + TreeSize(root->right) + 1;int TreeSize(BTNode* root)
{// 当root == NULL为真，则返回0；当root == NULL为假则返回TreeSize(root->left) + TreeSize(root->right) + 1return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
}

4.2.3 二叉树叶子节点的个数

// 叶子节点也就是度为0的节点，即左子树和右子树都为空树的节点
// 整个二叉树的叶子节点，
// 先判断根是不是叶子节点，
// 再判断左子树的叶子结点和右子树的叶子节点，层层递归就可以了int TreeLeafSize(BTNode* root)
{// 当节点为空树时就会返回if (root == NULL)  return 0;// 当root->left == NULL && root->right == NULL为真，说明当前节点为叶子节点if (root->left == NULL && root->right == NULL)  return 1;// 递归// 返回左子树叶子结点的个数 + 右子树叶子结点的个数return TreeLeafSize(root->left) + TreeLeafSize(root->right);  
}

4.2.4二叉树的深度（层数）

// 判断整个二叉树的深度
// 先判断左子树的深度
// 再判断右子树的深度
// 将深度更大的一方加上根节点的深度（也就是1），层层递归之后就是整个二叉树的深度，int TreeHeight(BTNode* root)
{// 遇到空节点则返回if (root == NULL)return 0;int lh = TreeHeight(root->left);int rh = TreeHeight(root->right);// 如果左子树的高度大于右子树的高度，那么就返回lh + 1// 反之，返回rh + 1return lh > rh ? lh + 1 : rh + 1;
}

4.2.5 二叉树第k层节点的个数

// 第K层节点个数
// 也就是左子树第k-1层的节点个数   +     右子树第k-1层的节点个数
// 层层递归就可以了int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;// 当k == 1，也就是递归到了最后一层，返回当前节点的数量（也就是1）if (k == 1)   return 1;// 将整棵树第k层节点的个数转换成求子树第k-1层节点的个数return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

4.2.6 二叉树查找值为x的节点

// 二叉树查找值为x的节点// 返回x所在的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{BTNode* lret, *rret;// 1.先判断当前节点是否为空，如果为空就返回if (root == NULL)return NULL;// 2.判断根节点是否为值为x的节点，如果是就返回if (root->data == x)return root;// 先去左树找// 判断左子树是否为x的节点，如果是就返回lret = TreeFind(root->left, x);if (lret)return lret;// 左树没有找到，再到右树找// 判断右子树是否为x的节点，如果是就返回rret = TreeFind(root->right, x);if (rret)return rret;// 左右子树都没有，那么就返回空return NULL;
}

5. 二叉树基础oj练习

1.单值二叉树。Oj链接

bool isUnivalTree(struct TreeNode* root){// 先判断根是否为空，为空则为真，返回if(root == NULL)return true;// 再判断根节点的值是否与左子树节点的值相等，且先要保证左子树节点不为空// 1.保证左子树节点不为空// 2.保证根节点的值 与 左子树节点的值相等// 如果不相等，则为假，直接返回if(root->left && root->val != root->left->val)return false;// 再判断根节点的值是否与右子树节点的值相等，且先要保证右子树节点不为空// 1.保证右子树节点不为空// 2.保证根节点的值 与 右子树节点的值相等// 如果不相等，则为假if(root->right && root->val != root->right->val)return false;// 如果左子树和右子树节点的值都与根节点相等，则往下递归// 且必须左右子树都为真，最终结果才为真return isUnivalTree( root->left) && isUnivalTree( root->right);}

2.检查两颗树是否相同。OJ链接

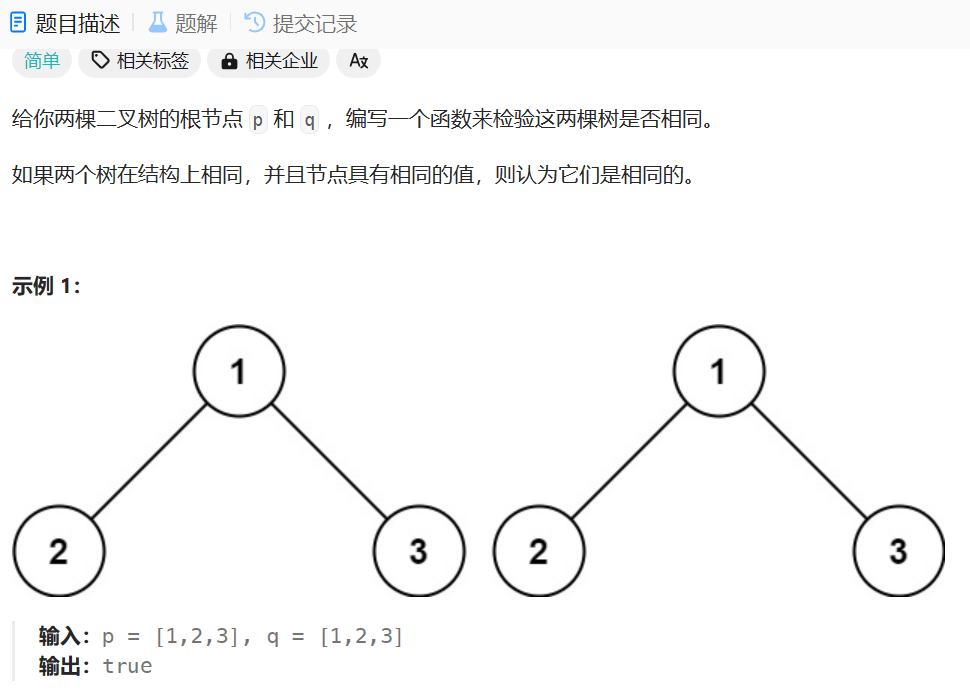
// 用分治的思想
bool isSameTree(struct TreeNode* root1, struct TreeNode* root2){// 情况一：根节点都为空；那么两棵树必然相同，则返回真if(root1 == NULL && root2 == NULL)return true;// 情况二：其中一个根节点为空// ||操作符，表达式1为真，则不用判断表达式2，直接进入if(root1 == NULL || root2 == NULL)return false;// 情况三：比较根节点的值是否相等if(root1->val != root2->val)return false;// 满足以上条件，再递归，必需左右子树都为真，总体才为真return  isSameTree(root1->left,  root2->left) && isSameTree(root1->right,  root2->right);
}

3. 对称二叉树。OJ链接

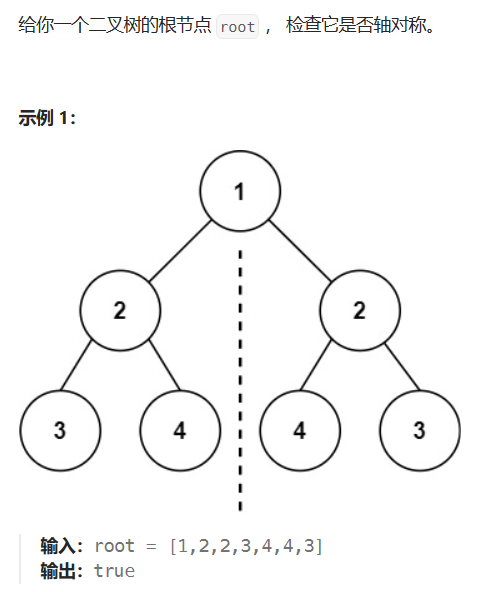
// 辅助函数，递归检查两个树的节点是否对称
bool isSymmetricHelper(struct TreeNode* leftNode, struct TreeNode* rightNode) {// 如果两个节点都为空，则对称if (leftNode == NULL && rightNode == NULL) {return true;}// 如果其中一个节点为空，另一个不为空，则不对称if (leftNode == NULL || rightNode == NULL) {return false;}// 如果两个节点的值不相等，则不对称if (leftNode->val != rightNode->val) {return false;}// 递归比较左子树的左节点与右子树的右节点，以及左子树的右节点与右子树的左节点return isSymmetricHelper(leftNode->left, rightNode->right) && isSymmetricHelper(leftNode->right, rightNode->left);
}// 主函数，检查二叉树是否轴对称
bool isSymmetric(struct TreeNode* root) {// 空树是对称的if (root == NULL) {return true; }// 调用辅助函数检查左右子树的对称性return isSymmetricHelper(root->left, root->right);
}

4. 二叉树的前序遍历。 OJ链接

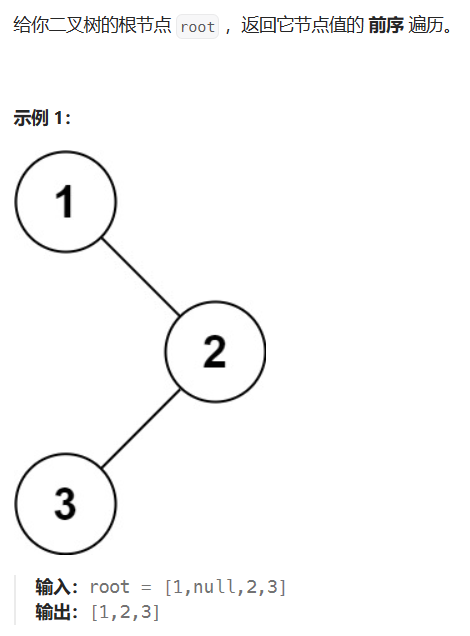
// 这个函数可以返回二叉树节点的个数
int TreeSize(struct TreeNode* root)
{if(NULL == root){return 0;}return 1 + TreeSize(root->left) + TreeSize(root->right);
}//此处i必须进行传址调用，如果是传值调用，遍历完左子树之后，回归到根节点，i的值不会发生改变
void preorder(struct TreeNode* root, int* a, int* pi)
{if(NULL == root){return;}// 前序遍历// 1.先遍历根节点，将根节点的数据存储到数组a中a[*pi] = root->val;printf("a[%d] = %d\n", *pi, a[*pi]);//用于调试(*pi)++;// 2.遍历左子树，遍历右子树preorder(root->left, a, pi);preorder(root->right, a, pi);}/***Note: The returned array must be malloced, assume caller calls free().如果调用方调用free()，则返回的数组必须是错误的。*/
int* preorderTraversal(struct TreeNode* root, int* returnSize){// 先确定要malloc的空间的大小int n = TreeSize(root);// n也就是数组的大小，通过输出参数将其返回*returnSize = n;printf("size = %d\n", n);//用于调试int* a = (int*)malloc(sizeof(int)*n);// 再写一个前序遍历，每遍历一个数，就将其存储到数组a中// i就是根节点的下标int i = 0;preorder(root, a, &i);return a;
}

7. 另一颗树的子树。OJ链接

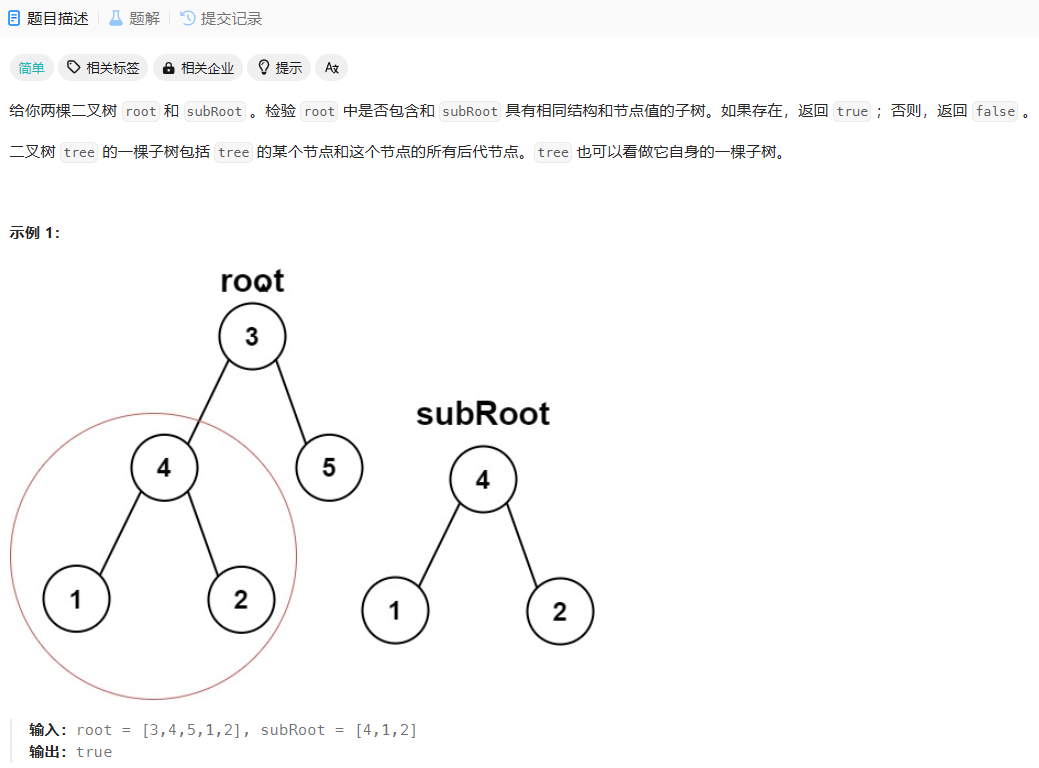
// 用分治的思想
bool isSameTree(struct TreeNode* root1, struct TreeNode* root2){// 情况一：根节点都为空if(root1 == NULL && root2 == NULL)return true;// 情况二：其中一个根节点为空// 通过情况一：说明两个根不可能同时为空；if(root1 == NULL || root2 == NULL)// ||操作符，表达式1为真，则不用判断表达式2，直接进入return false;// 情况三：比较根节点的值是否相等if(root1->val != root2->val)return false;// 满足以上条件，再递归，必需左右子树都为真，总体才为真return  isSameTree(root1->left,  root2->left)&& isSameTree(root1->right,  root2->right);
}// 将根节点传给函数isSameTree()进行比较，如果不相等
// 再将左子树的节点和右子树的节点传过去，只要有一个满足条件，则为真
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){// 由题可知两棵树都不是空树，但是root会递归，因此当root为空时，root没有子树了，也就是不包含subroot这个子树if(root == NULL)return false;// 通过函数isSameTree(root,subRoot)可以判断出，以root和subroot为根节点的两棵树是否相同if(isSameTree(root,subRoot))return true;// 递归（判断左右子树，是否包含subroot）return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);}

6.二叉树的创建和销毁

二叉树的构建及遍历。OJ链接

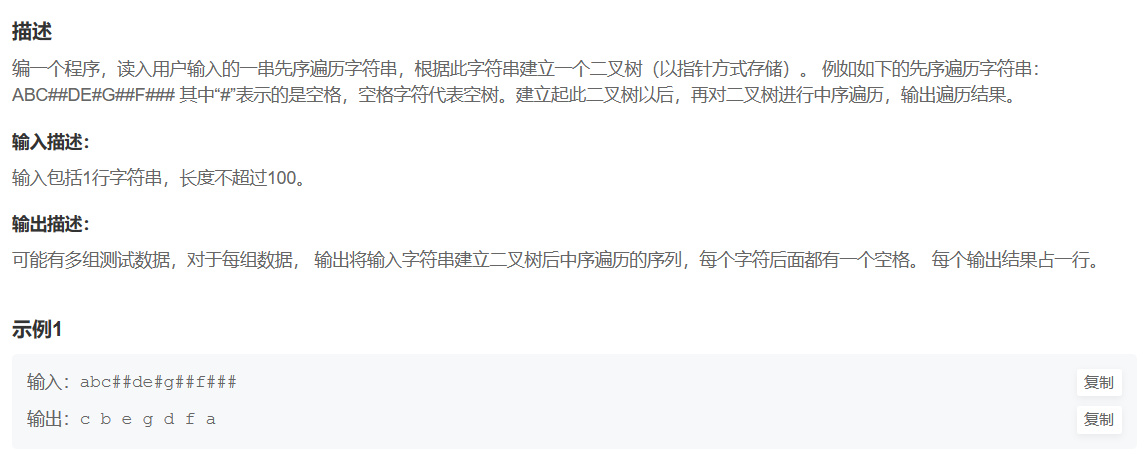
#include<stdio.h>
#include<stdlib.h> //malloc的头文件// 二叉树节点的结构体
typedef char BTDataType;
typedef struct Node
{int val;// 左子树的指针struct Node* left;// 右子树的指针struct Node* right;
}BTNode;                  // 将这个结构体重新定义为BTNodBTNode* BinaryTree(BTDataType* str, int* pi)
{// 如果为'#'也就是到了空树，直接返回;相当于前序遍历中判断是否为空树，if(str[*pi] == '#'){//将指针调整到下一个字符(*pi)++;return NULL;}// 如果不是'#'再按照前序遍历的循序malloc空间，再将其存储到二叉树的节点中BTNode* root = (BTNode*)malloc(sizeof(BTNode));if(root == NULL){perror("malloc fail");exit(-1);}// malloc成功之后，就可以将字符进行储存，储存之后，将字符的指针，调整到下一个字符root->val = str[*pi];(*pi)++;// 遍历完根之后，再遍历左子树，需要将开辟的左子树的地址返回，这样根节点才可以找到左子树root->left = BinaryTree( str, pi);root->right = BinaryTree( str, pi);// 层层递归，最终得到前序遍历顺序的二叉树// 得到二叉树之后，再将二叉树根节点的地址返回，以便调用者访问return root;
}// 通过这个函数来中序遍历二叉树，并进行打印
void inorder(BTNode* root)
{if(NULL == root){return;}// 先访问左子树inorder(root->left);// 打印根printf("%c ", root->val);// 再访问右子树inorder(root->right);// 层层递归，会将左右子树的根都打印}int main()
{// 创建一个容量为100的数组// 并输入n个字符BTDataType str[100] = {0};scanf("%s", str);// 通过前序遍历的方法来创建一个二叉树// i用来记录数组的下标，必须进行传址调用，// 如果是传值调用，左子树递归完，返回之后i的值没有发生改变，无法再完成右子树的递归int i = 0; // 通过函数BinaryTree()来创建一个二叉树（前序遍历的顺序），并返回这个二叉树的根节点BTNode* root = BinaryTree(str, &i);// 二叉树创建好之后，再按照中序遍历的顺序进行打印inorder(root);return 0;
}

二叉树的销毁

// 用后续遍历的思想来销毁二叉树void BinaryTreeDestroy(BTNode* root)//因为传的是一级指针，所以需要调用者自己将root置空
{if (root == NULL){return;}BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);
}

7.二叉树的层序遍历

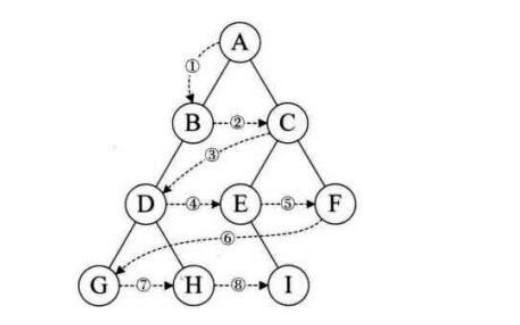
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在

层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层

上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

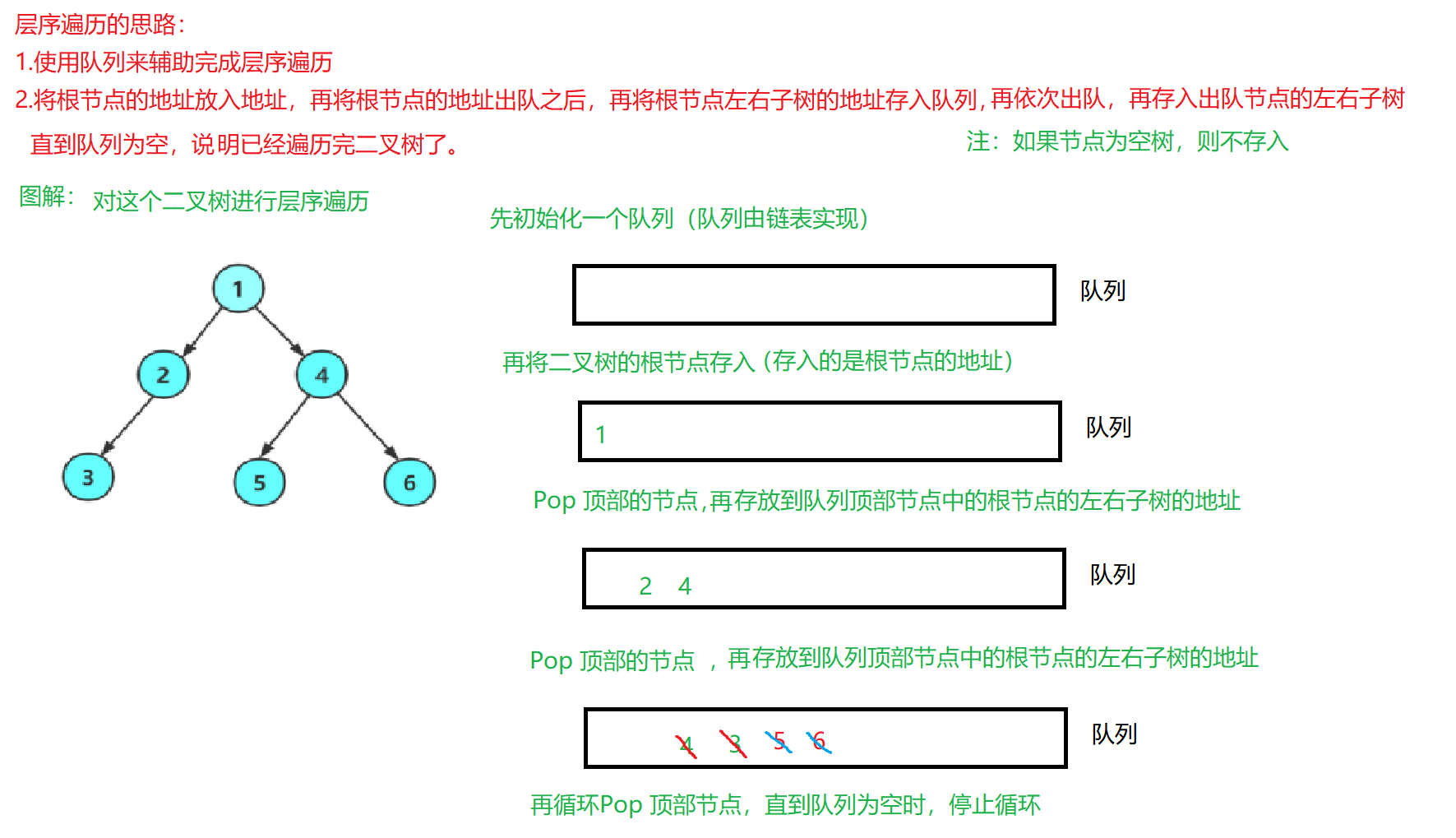
// 通过这个函数来层序遍历二叉树
void TreeLevelOrder(BTNode* root)
{// 创建一个队列Queue q;// 初始化一个队列QueueInit(&q);// 1.根节点如果不为空，那么就将根节点放入道队列中if (root)QueuePush(&q, root);// 当队列为空，说明已经层序遍历完了所有的节点while (!QueueEmpty(&q)){// 2.拿到堆顶根节点，再从队列中，将堆顶节点出队BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);// 3.判断拿到堆顶根节点的左子树和右子树是否为空树// 如果不是空树，那么就将这两个子树的根节点入队if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");// 销毁队列空间，防止内存泄漏QueueDestroy(&q);
}

• 注：使用的队列接口，是作者自定义的接口，在队列的模拟实现这篇文章中可以找到。

判断二叉树是否为完全二叉树

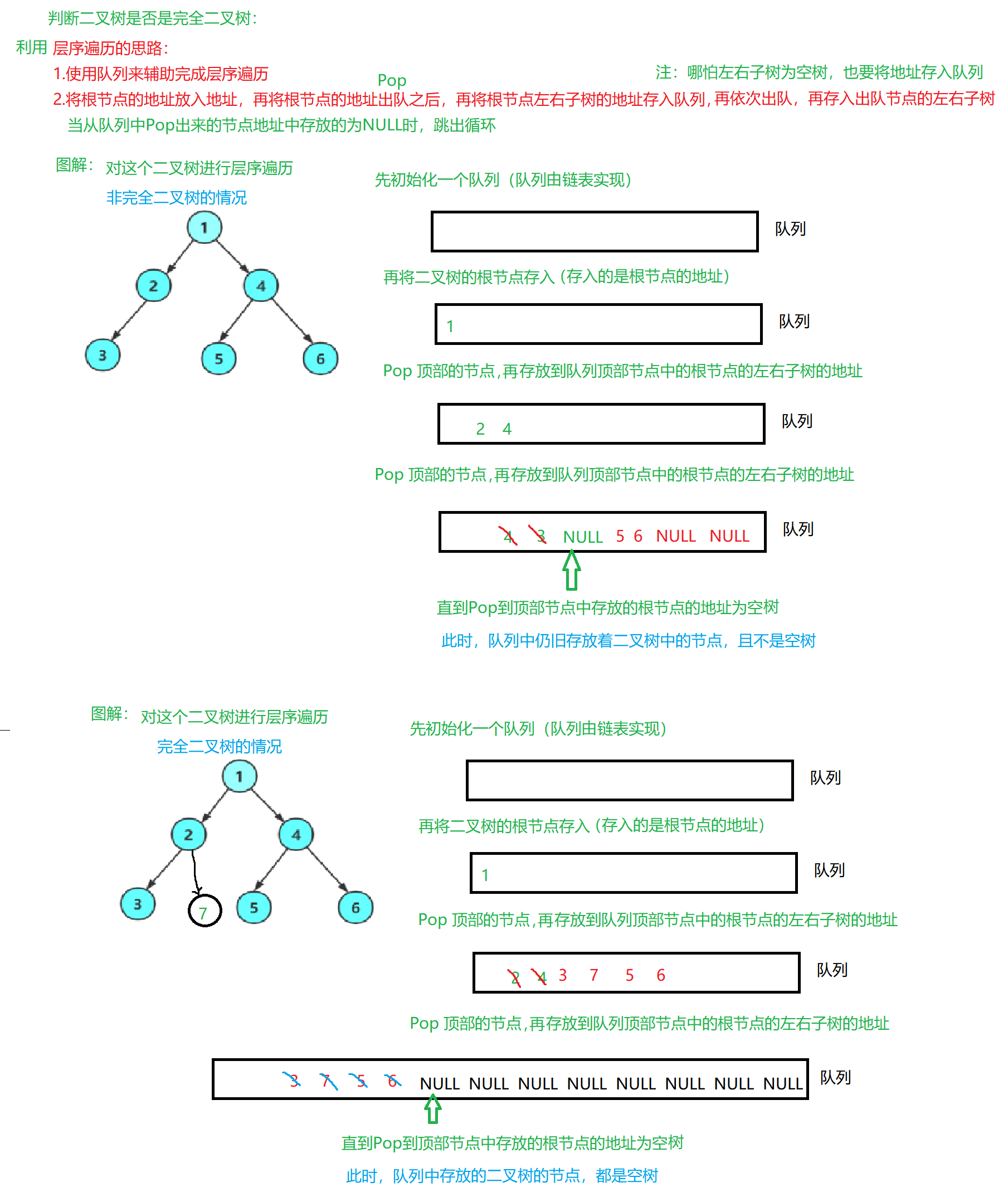
• 注：在上面这幅图中，第一种情况的二叉树就不是完全二叉树；第二种情况的二叉树才是完全二叉树

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);// 必须保证根节点不为空；空树一定不是完全二叉树if (root)QueuePush(&q, root);// 二叉树不是空树// 此时，层序遍历二叉树的节点，当出队的队顶元素为空时，循环结束（跳出循环）// 当队列中的节点为空，那么循环结束（已经遍历了所有节点）while (!QueueEmpty(&q)){// 拿到队顶的节点BTNode* front = QueueFront(&q);// Pop队顶的节点（出队队顶的节点）QueuePop(&q);// 只要队顶的节点中存放的二叉树的节点为空树，就跳出循环if (front == NULL){break;}// 将堆顶节点的左右子树入队QueuePush(&q, front->left);QueuePush(&q, front->right);}// 遇到空以后，后面全是空，则是完全二叉树// 遇到空以后，后面存在非空，则不是完全二叉树while (!QueueEmpty(&q)){// 依次出队队列元素，并判断其是否为空BTNode* front = QueueFront(&q);QueuePop(&q);// 如果存在非空，则不是完全二叉树if (front != NULL){//返回之前，为了防止内存泄漏，必须先销毁队列空间QueueDestroy(&q);return false;}}// 此时，可以保证这个二叉树就是完全二叉树// 返回之前，为了防止内存泄漏，必须先销毁队列空间QueueDestroy(&q);return true;
}