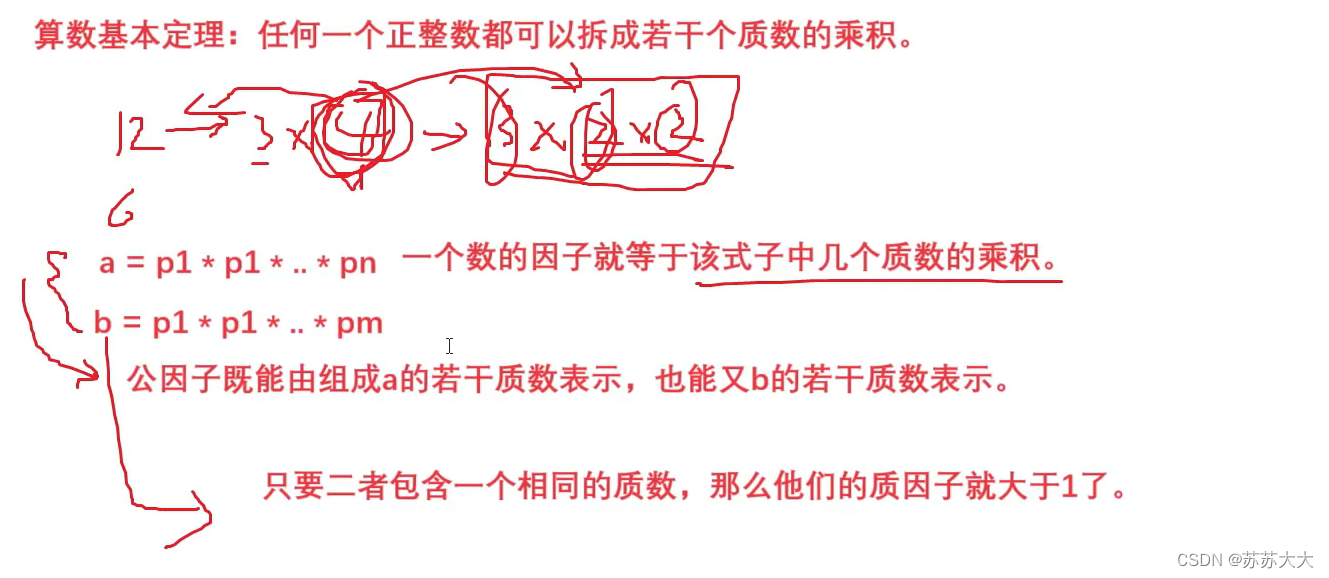
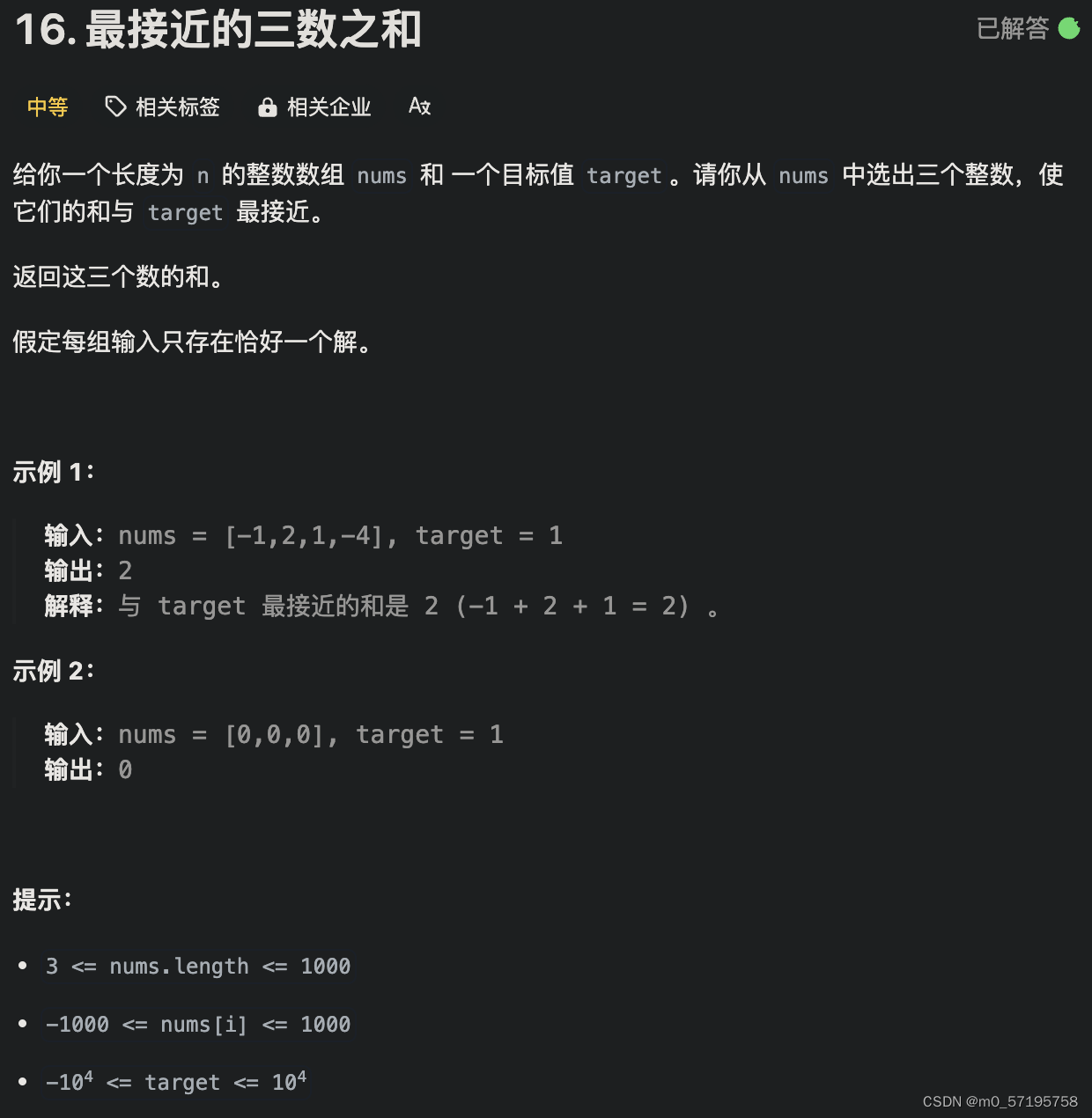
乳腺癌的非侵入性诊断程序涉及体检和成像技术,如乳房X光检查、超声检查和磁共振成像。成像程序对于更全面地评估癌症区域和识别癌症亚型的敏感性较低。
CNN表现出固有的归纳偏差,并且对于图像中感兴趣对象的平移、旋转和位置有所不同。因此,通常在训练CNN模型时应用图像增强。
Swin Transformer是视觉转换器的变体,基于非重叠移位窗口的概念,是一种用于各种视觉检测任务的成熟方法。
用于分类任务的VIT实现全局自我注意力,其中计算图像补丁和所有其他补丁之间的关联。这种全局量化导致了关于补丁数量的二次计算复杂性,使得它不太适合处理高分辨率图像。Swin Transformer工作在移位的窗口上,可以提供可变的图像补丁分辨率。
为了高效建模,提出并计算局部窗口内的自注意力,并且以不重叠的方式排列窗口以均匀划分图像。基于窗口的自注意力具有线性复杂性和可扩展性。基于窗口的自注意力的建模能力是有限的,因为它缺乏跨窗口的连接。因此,提出了一种移位窗口分区方法,在连续旋转变压器块的分区配置之间交替进行,以允许跨窗口连接,同时保持非重叠窗口的高效计算。
基于乳房x光检查
在从特定感兴趣区域(ROI)进行分类时,从乳房X光片中考虑的典型特征是肿块大小、ROI的不规则形状、ROI边界的均匀性和组织密度。将这些手工制作的特征输入到支持向量机、k近邻、逻辑回归、二叉决策树和人工神经网络等分类器中进行分类。
基于超声图像检查
超声检查也是非侵入性的,基于机器学习的方法包括基于感兴趣区域的放射性特征,用于使用各种机器学习分类器进行分类。使用希尔伯特变换和标记控制分水岭变换提取形状和纹理特征,并将其进一步馈送到KNN分类器和集成决策树模型。
基于组织病理学图像
非侵入性成像程序可能无法识别癌症区域及其亚型。为了弥补这一缺陷,活检被用于更多样化地研究乳腺组织中的恶性肿瘤。活检包括收集样本并在显微镜载玻片上对组织进行染色,以便更好地观察细胞质和细胞核。
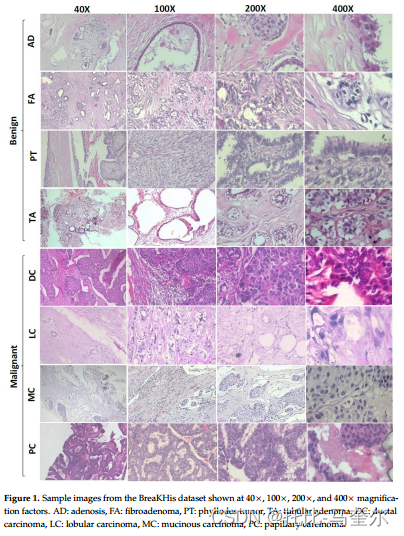
BreakHis数据集
BreaKHis数据集由82例患者的乳腺肿瘤手术活检获得的7909张显微RGB图像组成,放大倍率分别为50倍、100倍、200倍和400倍。数据包括良性和恶性亚型。此外,良性癌症亚型包括纤维腺瘤、管状腺瘤、叶状瘤和腺病,而恶性亚型包括导管癌、乳头状癌、小叶癌和粘液性癌。
Swin Transformer
准备工作
- 将700*640的原始图像分辨率调整为224*224
- 将输入尺寸为
的RGB图像将原始的起始补丁大小分割成大小为4*4的小补丁
- 每个图象补丁的尺寸为
- 在大小为48的原始特征张量上应用线性嵌入层,将其投影到特征维度C上
体系结构
- 将尺寸为C的补丁线性嵌入上应用几个具有自注意力的Swin Transformer块,保证tokens的数量为
,线性嵌入层与Swin Transformer一起构成Swin Transformer体系结构的第一阶段。
- 为了便于分层表示,从Swin Transformer Block架构的第二阶段开始,通过补丁合并层来降低补丁的数量。第二阶段的补丁合并层将每组2*2相邻补丁的特征进行拼接,并在4C维拼接特征上应用线性层。这样可以将补丁的数量减少了4倍,并且将线性层的输出维度为2C,第二阶段的输出补丁数保持在
,
- 这样的过程重复两次,构成阶段3和阶段4.导致其输出分辨率分别为
和

模型交叉验证和测试
原始数据集中图像的强度值在0 ~ 255之间,将这些强度缩放为−1和1之间的值。当包含所有缩放因子的图像时,数据集被分为62:8:30分别用于训练、验证和测试。当从特定缩放因子的图像中实现分类时,遵循72:8:20的分割。通过经验选择Swin Transformer的超参数,并使用验证集来确保模型不会过拟合。


![[挖坟]如何安装Shizuku和LSPatch并安装模块(不需要Root,非Magisk)](https://img-blog.csdnimg.cn/direct/00ba67dd82014123b99265c133e5afaf.png)