三次 Bspline(B样条曲线) NURBS曲线的绘制 matlab

先来了解几个概念：

1.1 节点向量：

B-Spline需要定义曲线的节点向量U，它可以对应到Bezier曲线的参数u。

其元素个数 (m+1) 和曲线阶数 k 、控制点个数n满足：m+1=k+1+n+1

如果U的每段的距离是相等，那么这个B-Spline就被称为均匀B样条，即：

如果U向量中存在k个相等的元素，则 B-spline 具有 k 的重复度；

1.2 权因子：

2 NURBS的计算公式：

NU-nouniform，即非均匀，指有效节点向量区间距离非减不相等的。
R-rational，有理，指权值（weight）各不相等。权值代表各控制点对某一个拟合点的影响力，这里也可以发现普通的样条来说，各控制点对于同一个拟合点的影响力是相等的。
BS-BSpline，B样条

一条k次NURBS曲线可以表示为一分段有理多项式矢函数，具有如下形式：

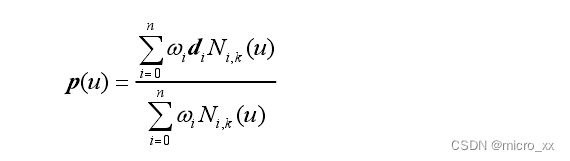
式中：

常取两端节点的重复度为k+1，在很多实际应用中，端节点值常取 0、1。

为了在方便进行MATLAB计算和编程，将推导实践中较为常用的三次NURBS曲线曲面的矩阵表达形式。

3 NURBS曲线的矩阵表达：

当k=3时，可以写出第 i 段 NURBS 曲线矩阵形式为：

式中：

3.1 权因子的选择与确定是一个至今尚未彻底解决的问题：

权因子对曲线的影响

3.2 节点矢量计算：

节点总数为：n+k+2，节点矢量的最大下标为：n+k+1；

常取两端节点的重复度为k+1，若k=3，则左边k+1个0，右边k+1个1。

内节点的数目为n-k，因此曲线的段数为n-k+1;

如果已知型值点，即曲线上的点可以通过积累弦长、向心法进行节点矢量的计算，但是现在我们仅仅给定控制点和次数，根据这个来确定节点矢量有：

若是奇次，则为：

具体地，若k=3,则：

显然若k=3：

分母为n-k+1段三次曲线相应的控制多边形的总长度L;

u4为第一段三次曲线相应的控制多边形的长度之和/L;

u5为(第一段三次曲线相应的控制多边形的长度之和+第二段三次曲线相应的控制多边形的长度之和)/L;

......

u8为(第一段+第二段+第三段+......+第8-k段三次曲线相应的控制多边形的长度之和)/L;

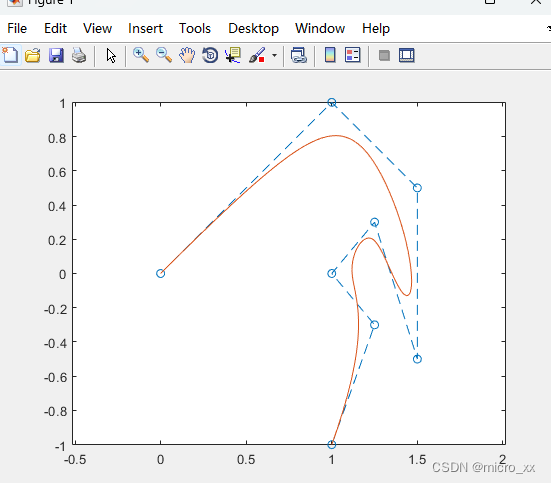
clc
clear% 选定控制点
P =[0,0;1,1;1.5,0.5;1.5,-0.5;1.25,0.3;1,0;1.25,-0.3;1,-1;];
[row,col] = size(P);
n = row - 1;
m = col;
% 权因子
w = [1;2;3;4;5;6;7;8;];
% 1.计算节点矢量
l = sqrt((P(1:end-1,1)-P(2:end,1)).^2+(P(1:end-1,2)-P(2:end,2)).^2);
L = l(1)+2*l(2)+3*sum(l(3:end-2))+2*l(end-1)+l(end);k = 3;
U = zeros(n+k+2,1);
U(1:k+1) = 0;
U(end-(k):end) = 1;
lsumtemp = 0;
for ik = k+2:n+k+2-(k+1)ik1 = ik - (k+2) +1;lsumtemp = lsumtemp + l(ik1) + l(ik1+1) +l(ik1+2);U(ik) = lsumtemp/L;
endi = 1:n-k+1;
detai_1_3(1,1,i) = U(i+1+3) - U(i+1);
detai_2_1(1,1,i) = U(i+2+1) - U(i+2);
detai_2_2(1,1,i) = U(i+2+2) - U(i+2);
detai_2_3(1,1,i) = U(i+2+3) - U(i+2);
detai_3_1(1,1,i) = U(i+3+1) - U(i+3);
detai_3_2(1,1,i) = U(i+3+2) - U(i+3);
detai_3_3(1,1,i) = U(i+3+3) - U(i+3);
m14(1,1,i) = 0; m24(1,1,i) = 0; m34(1,1,i) = 0;
m11(1,1,i) = detai_3_1.^2./(detai_2_2.*detai_1_3);
m13(1,1,i) = detai_2_1.^2./(detai_2_2.*detai_2_3);
m23(1,1,i) = 3*detai_3_1.*detai_2_1./(detai_2_2.*detai_2_3);
m33(1,1,i) = 3*detai_3_1.^2./(detai_2_2.*detai_2_3);
m44(1,1,i) = detai_3_1.^2./(detai_3_2.*detai_3_3);
m43(1,1,i) = -(m33(1,1,i)/3+m44(1,1,i)+detai_3_1.^2./(detai_3_2.*detai_2_3));M1 = [m11,   1-m11-m13,m13,m14;-3*m11, 3*m11-m23,m23,m24;3*m11,-3*m11-m33,m33,m34;-m11, m11-m43-m44,m43,m44;];t_p = linspace(0,1,100)';
T_p = [ones(length(t_p),1),t_p,t_p.^2,t_p.^3];
T = repmat(T_p,1,1,length(m11));xo = P(:,1);
Dw_xt = [w(i).*xo(i),w(i+1).*xo(i+1),w(i+2).*xo(i+2),w(i+3).*xo(i+3)]';
yo = P(:,2);
Dw_yt = [w(i).*yo(i),w(i+1).*yo(i+1),w(i+2).*yo(i+2),w(i+3).*yo(i+3)]';
W_t = [w(i),w(i+1),w(i+2),w(i+3)]';
Dw_x = reshape(Dw_xt,4,1,5);
Dw_y = reshape(Dw_yt,4,1,5);
W = reshape(W_t,4,1,5);for ink = 1:n-k+1dem(:,ink) = T(:,:,ink)*M1(:,:,ink)*W(:,:,ink);xp_i(:,ink) = T(:,:,ink)*M1(:,:,ink)*Dw_x(:,:,ink)./dem(:,ink);yp_i(:,ink) = T(:,:,ink)*M1(:,:,ink)*Dw_y(:,:,ink)./dem(:,ink);
end
xp = xp_i(:);
yp = yp_i(:);
C_u = [xp,yp];figure(1)
plot(P(:,1),P(:,2),'--o')
hold on
plot(C_u(:,1),C_u(:,2))
axis equal